期权动态套期保值双相机决策模型及实证研究

余 星，张卫国，刘勇军

华南理工大学 工商管理学院，广州 510640

期权动态套期保值双相机决策模型及实证研究

余 星，张卫国，刘勇军

华南理工大学 工商管理学院，广州 510640

金融市场具有多变性，投资者一般需要根据市场情况动态地改变套期保值策略，使套期保值组合价格波动的风险被对冲掉。因此，有必要建立期权动态套期保值模型，得到动态的最优期权头寸，这意味着投资者需要按照模型所得到的头寸动态调仓才能达到风险最小的目的。然而，买入期权进行套期保值需要支付期权金成本，也就是投资者为了达到风险最小化的目的需要付出成本代价。那么，付出的代价是否“划算”是投资者面临的一个问题。此外，买入欧式看跌期权可以规避现货价格下跌的风险，但欧式期权只有到到期日时才能被执行，而投资者不一定要持有期权直到到期日。于是，投资者在投资期间选择何时退出是期权动态套期保值的另一个问题。

针对传统的期权套期保值策略存在错失退出良机和调仓过于频繁的问题，提出退出和调仓双相机决策准则，进一步优化传统套期保值策略。在满足预算、预期收益、头寸约束条件下，建立基于在险价值的最优期权动态套期保值模型，得到传统动态套期保值策略。在此基础上，基于经济价值视角将风险和成本代价统一化度量，利用期末绩效评价提出退出和调仓双相机决策准则，进一步修正期权套期保值策略。利用上证50ETF及以上证50ETF为标的的期权开展实证研究。

研究结果表明，运用退出相机准则提供了提前退出投资的参考时间点，运用调仓相机准则通过减少不必要的调仓降低调仓成本。通过对比发现传统的期权动态套期保值策略存在缺陷，运用双相机抉择的期权套期保值策略能够获得更有效率的套期保值结果。利用退出相机提供7个参考退出交易日，若在这些交易日选择退出，投资者将获得比较大的利润，利用调仓相机后增加了收益。

考虑双相机决策的期权最优套期保值模型改进了传统模型的单一决策，提出了更有效的风险控制策略，为投资者提供决策参考具有实际意义。

期权动态套期保值；退出相机准则；调仓相机准则；在险价值；经济价值

1 引言

2015年2月9日，上证50ETF期权作为中国第一个场内期权在上海证券交易所上市，这不仅宣告了中国期权时代的到来，也意味着中国已拥有全套主流金融衍生品。随着上证50ETF期权的推出，除期货外投资者又有了一种新的套期保值工具可供选择。与期货的线性损益曲线相比，期权作为一个非线性金融衍生工具，与现货构造保值策略时和单纯地用期货套期保值有很大区别，用期货保值最多可以获取一些边际利润，但是用期权套期保值可能会获取超额利润。因此，利用期权进行套期保值受到投资者的青睐。

为了对冲现货头寸的风险，期权套期保值的关键问题是如何动态地选择合适的期权头寸对现货进行保值。首先，不同于期货套期保值，买入期权进行套期保值需要支付期权金。因此，需要在成本等约束条件下建立合适的期权动态套期保值模型，得到传统意义上的最优期权头寸。其次，若在投资期间出现了利好机会，从风险规避角度，适时止盈是非常有必要的。同时，有关研究表明不一定要完全接受动态策略，特别是有些调仓策略会带来很高的交易成本时，若仍按最优套期保值模型求解出的头寸调仓，可能会出现得不偿失的后果。所以，如何结合期权的特点，建立退出相机准则和调仓相机准则确定每个投资时刻是否退出、是否进行调仓是一个现实问题。为此，本研究从经济价值这个新视角建立期权动态套期保值双相机决策模型，为期权最优套期保值问题研究提供新思路。

2 相关研究评述

一直以来，利用期权、期货等衍生工具进行套期保值是非常重要的风险管理方法。目前，期货套期保值的研究取得了丰富的成果，利用期货管理风险的理论也比较成熟，主要集中于建立模型解决最优期货头寸问题。大部分学者建立波动率模型，研究期货套期保值基差最小化问题。DARK[1]提出期货套期保值的FIEGARCH和FIAPARCH模型；ZHOU[2]通过实证对比研究各种套期保值模型的效率；谢赤等[3]采用中国市场现货价格和期货价格数据， 较全面地对比分析M-Copula-GJR-VaR模型与CCC-GARCH-VaR模型、DCC-GARCH-VaR模型、Clayton Copula-GJR-VaR模型、Gumbel Copula-GJR-VaR模型的套期保值比率和套期保值效果；孙艳等[4]建立UHF-EGARCH模型对股指期货市场进行实证研究。也有一些学者从交易风险角度建立期货套期保值模型。傅俊辉等[5]考虑规避现货价格风险和逐日盯市风险，建立期货套期保值模型。更多相关研究可以参考PARK et al.[6]、WEI et al.[7]和HOU et al.[8]的研究。相对而言， 期权套期保值的研究就显得比较薄弱。与期货套期保值类似，为了对冲现货头寸的风险，期权套期保值的关键问题是如何选择合适的期权头寸对现货进行保值。而期权套期保值主要有两个不同之处，①以投资者希望规避现货价格下跌而买入看跌期权套期保值为例，买入期权需要支付期权金。②欧式期权只有到到期日时才能被执行，而投资者不一定要持有期权直到到期日。因此，结合期权的特点，建立有效的套期保值决策准则具有实际意义。

很多学者把期权当成资产融入到投资组合中，研究期权在最优投资组合中的应用问题。SCHEUENSTUHL et al.[9]在预算、方差效率和缺口约束下，建立组合末期收益最大化的股票和期权组合模型；WANG et al.[10]研究期权风险中性对冲问题，提出期权定价的混合对冲策略。这些研究本质上将期权视为一种新的资产进行投资组合，而ARAI[11]、KALLSEN et al.[12]和LIANG et al.[13]则利用对冲原理对期权进行风险中性定价研究。在这些研究中，期权头寸和现货头寸都变化，与传统意义上现货头寸不变、只调整期权头寸的套期保值有区别。从保持现货头寸不变的角度，有学者比较了期权与期货套期保值的效果。WONG[14]研究竞争出口公司利用期权与期货对冲汇率风险的最优决策问题，得到当价格风险与汇率风险负相关时，多头看跌期权是最优的；进一步地，研究状态依赖偏好下竞争性出口公司利用期权套期保值的优势[15]。这些研究中在一般效用函数下推导出期权最优头寸满足的不等式，从理论上分析最优头寸满足的条件，没有给出期权头寸的表达式。FRECHETTE[16]、TOPALOGLOU et al.[17]和BAJO et al.[18]也都利用期权、期货套期保值研究竞争性出口公司最优生产决策问题。在实证研究方面，LIEN et al.[19]基于下偏矩风险比较货币期货与货币期权套期保值的对冲效率；BAJO et al.[20]考虑公司生产和基差风险，建立企业最优期权套期保值模型，发现套期保值的投入影响敲定价格，生产效率影响对冲效率，基差风险影响最优合约的选择。中国学者对期权套期保值也做了一些理论研究，杨春鹏[21]利用概率方法研究以期权为套期保值工具的套期保值比率，在限定亏损概率条件下得出具体的套期保值比率；尹力博等[22]建立整体风险控制和后验优化风险再调整的外汇期权组合风险综合管理机制，研究人民币外汇期权的套保价值及最优套期保值策略。这些研究都是在静态情形下研究套期保值问题，而在实际投资中市场总是在变化的，投资者一般都会根据实际情况进行动态决策。

在套期保值问题研究中，风险度量测度的选择也是学者们关注的一个焦点问题。MELNIKOV et al.[23]利用复制未定权益方法建立期权CVaR动态套期保值模型；CAPINSKI[24]建立看跌期权组合对冲股票头寸CVaR风险的套期保值模型，解析地推导出期权CVaR动态套期保值头寸的显示表达式，并通过实例进行验证。他们的计算结果与MELNIKOV et al.[23]的结果非常接近。孙燕红等[25]以在险价值最小化为目标，结合波动率预测建立股指期货套期保值模型。CAPINSKI[24]解决动态套期保值的思路给本研究提供了启示，本研究建立基于在险价值最小化期权动态套期保值模型，得到传统套期保值期权头寸。

综上所述不难发现，目前关于套期保值问题的研究主要聚焦在如何选择对冲头寸上。但有关研究表明不一定要完全接受动态策略，特别是有些调仓策略会带来很高的交易成本时，若仍按最优套期保值模型求解出的头寸调仓，可能会出现得不偿失的后果。LIU et al.[26]将LENCE[27]和FLEMING et al.[28]提出的经济价值概念应用于套期保值问题中，通过比较经济价值和交易成本给出是否动态调整策略，对整个持有期内规避组合风险与产生的交易费用进行博弈。NOLTE et al.[29]将具有已实现跳的波动率经济价值应用到投资组合模型中，处理方法与FLEMING et al.[28]类似。彭红枫等[30]也运用经济价值建立期货动态调仓相机抉择模型。这些研究中的调仓相机准则都是基于期初绩效评价，而期初绩效评价不适用于欧式期权套期保值情形。因为投资者更关注到期日时的套期保值效果，因此在期权套期保值的研究中，需要将期初绩效评价推广到期末绩效评价。除调仓相机外，一般情况下，投资者都会根据市场状态等因素灵活做出投资决策。以持有现货头寸的投资者为例，买入看跌期权组合规避价格下跌的风险，当在投资期内出现了利好机会(如标的资产价格大涨)，从风险规避角度，投资者适时止盈也是非常必要的。关于期权套期保值退出相机问题的研究非常少，特别是从经济价值角度考虑的研究几乎没有。在刻画套期保值风险方面，传统的方差并非度量风险的优良指标。

本研究建立基于在险价值最小化期权动态套期保值模型，将模型转化为线性优化模型，给出期权头寸的显示表达式。利用经济价值进一步讨论期权套期保值退出和调仓双相机抉择问题，提出期权动态套期保值双相机准则。结合上证50ETF期权进行实证对比研究，根据退出相机准则给出适时退出投资的参考时间点；根据调仓相机准则降低调仓频率，减少调仓成本。本研究提出的双相机期权套期保值决策模型可以为投资者提供更有效的套期保值策略，也为期权最优套期保值问题研究提供新思路。

3 基于在险价值的期权最优动态套期保值模型

风险最小型期权动态套期保值主要是在约束条件下通过最小化一种具体风险测度函数得到期权头寸。常用的风险测度函数有方差、平均扩展吉尼系数和广义半方差等，但这些风险测度函数忽略了套期保值资产组合的期望回报率。为了解决这个问题，本研究采用在险价值(value at risk,VaR)作为套期保值组合的风险测度函数。VaR是指在一定置信水平下，某资产组合在未来特定的一段时间内的最大可能损失，可表示为

Pr(ΔL≤-VaRα)=1-α

(1)

其中，ΔL为套期保值组合在持有期Δt内的损失，VaRα为置信水平α下的在险价值，α为置信水平。基于VaR的期权最优套期保值原理是，首先在特定时间内和一定置信水平的前提下，确定每个期权头寸对应套期保值组合一个VaR风险值，然后对这个VaR风险值进行最小化，以得到最优套期保值策略。如果把套期保值组合收益看作随机变量，就可以用它的VaR度量组合风险水平。因此，首先需要描述套期保值组合资产价格过程。本研究假设标的资产价格服从几何布朗运动，数学描述为

dSt=μtStdt+σtStdZt

(2)

其中，t为时刻，St为标的资产价格，μt为标的资产在t时刻的瞬时漂移率，σt为波动率，Zt为标准布朗运动。设期权到期日T与投资期长相同，那么在t时刻剩余时间为τ，τ=T-t。由(2)式可得

ln(ST)～N(u，v2)

(3)

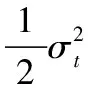
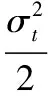
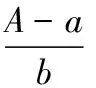
(4)

其中，E(PT)为期权在T时刻的期望价格；Φ(·)为标准正态分布的分布函数。

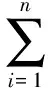
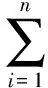
(5)

其中，Ki为第i个期权的敲定价格。记VaRα(Vt，τ)为在套期保值时间[t，T]内，以概率(1-α)保证套期投保者的损失不超过的值，于是有

Pr[Vt，T≥VaRα(Vt，τ)]=α

(6)

因此，将(5)式代入(6)式可得

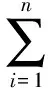
=α

(7)

将(7)式化简并取对数，有

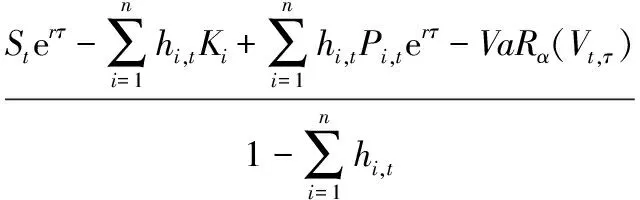
=α

(8)

根据(3)式得到套期保值组合的VaR风险为

(9)

与AHN et al.[31]假设常数(与时间无关)套期保值头寸不同，本研究的模型决策变量hi,t在不同的时刻动态变化。在t时刻，选择期权头寸hi,t，在满足买入期权成本预算和达到期望预期收益的约束条件下，使[t,T]时间内套期保值组合的VaRα(Vt，τ)最小，建立最优期权套期保值模型为

(P1)

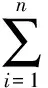
其中，Qt为t时刻买入期权的成本预算，Bt为t时刻最低预期收益。第3个约束条件为期权头寸满足的条件。

模型(P1)是一个线性规划模型，借助一般的线性规划软件非常容易求解出t时刻最优期权头寸hi,t，并基于它可以计算出[t,T]时间内套期保值组合的期望收益率Rt,T，即

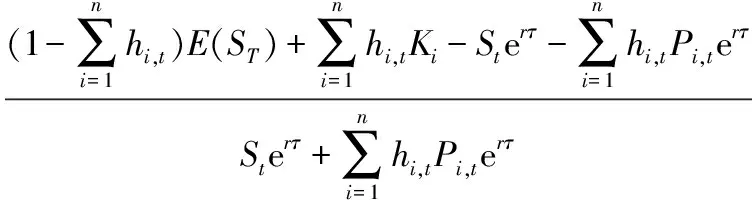
(10)

4 双相机决策准则

前面假设资产价格服从几何布朗运动，推导出套期保值组合VaR的表达式，并建立基于VaR的期权动态最优套期保值模型，通过求解模型可以得到期权最优头寸hi,t，投资者可以按照这个头寸进行动态决策。因为基于VaR的动态策略主要从套期保值组合的风险最小角度考虑，而期权不同于期货，买入看跌期权需要支付成本(期权金)，特别是有些调仓策略会带来很高的交易成本时，如果仍按最优套期保值模型求解出的头寸调仓，可能会出现得不偿失的后果。因此，需要在风险与调仓成本之间找到平衡，即调仓相机抉择。同样地，投资者买入看跌期权的初衷是预期在到期日时发挥期权的保护作用，对于持有现货的套期保值者而言，若在到期日前出现利好的机会，如标的资产价格大涨，那么投资者提前放弃期权直接卖出现货可能比一直持有到到期日更有利，投资者还面临着是否退出投资的抉择。因此，也需要在风险与退出代价之间找到平衡，即退出相机抉择。解决调仓相机抉择和退出相机抉择的关键是将风险和成本统一度量，为解决这个问题，本研究运用经济价值，提出期权套期保值双相机决策准则。

4.1 经济价值

首先，介绍经济价值的概念。FLEMING et al.[28]首次提出波动率经济价值概念。为了权衡规避组合风险与产生交易成本之间的关系，构建投资者的效用函数为

(11)

(12)

其中，Rd,t+1为动态策略下的收益率，Rs,t+1为静态策略下的收益率。当经济价值大于交易成本时，动态投资策略优于静态策略;当经济价值小于交易成本时，静态策略优于动态策略。

由(12)式可以看出，FLEMING et al.[28]提出的经济价值是相对于期初而言的。与FLEMING et al.[28]的期初评价不同，本研究考虑期权套期保值组合在期末时才体现价值的特点，提出期末绩效评价，并将已有的动、静态相机决策进行推广应用，分别构建退出相机决策准则和调仓相机决策准则。

4.2 退出相机决策准则

令Γt为t时刻投资者从一种策略(继续投资)转换到另一种策略(退出投资)愿意付出的成本，也称为经济价值。Γt>0表示改变决策愿意付出正的成本；Γt<0表示愿意付出负的成本，即要求正的收益。将Γt代入(12)式，得

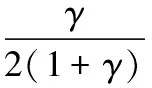
(13)

其中，Rd为不退出情形下套期保值组合的收益率，Rs为退出情形下套期保值组合的收益率。(13)式为本研究提出的退出相机准则满足的等式，通过求解(13)式可得Γt值。退出相机准则是本研究参考已有研究中调仓相机准则提出的一个新的决策准则。采用期末绩效评价法计算收益率，即

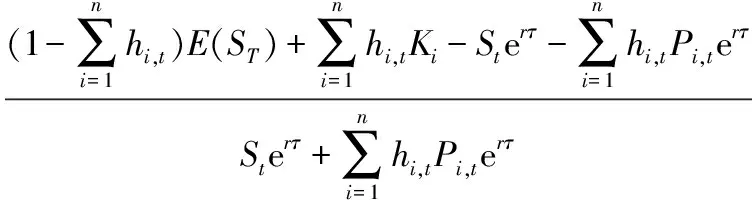
(14)

Rs=erτ-1

(15)

其中，hi,t为通过求解模型(P1)得到的期权头寸。(14)式本质上与(10)式一致，都是相对于T时刻的收益率。根据(13)式可以得到每个时刻退出与否的经济价值，设Dt为投资者从一种策略转换到另一种策略愿意付出的最大成本。通过比较Γt与Dt进行退出相机决策，若Γt>Dt，则投资者在t时刻选择退出；若Γt≤Dt，则投资者在t时刻选择继续投资，不退出。

4.3 调仓相机准则

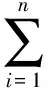
同样，t时刻的经济价值等式为

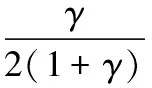
(16)

其中，Πt为t时刻调仓与否的经济价值，RY,t为t时刻进行动态调仓时套期保值的收益率，RN,t为t时刻不进行调仓时套期保值的收益率。具体为

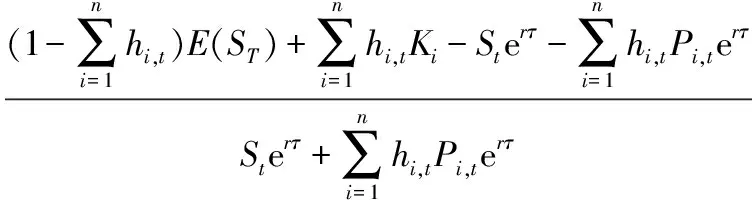
(17)

(18)

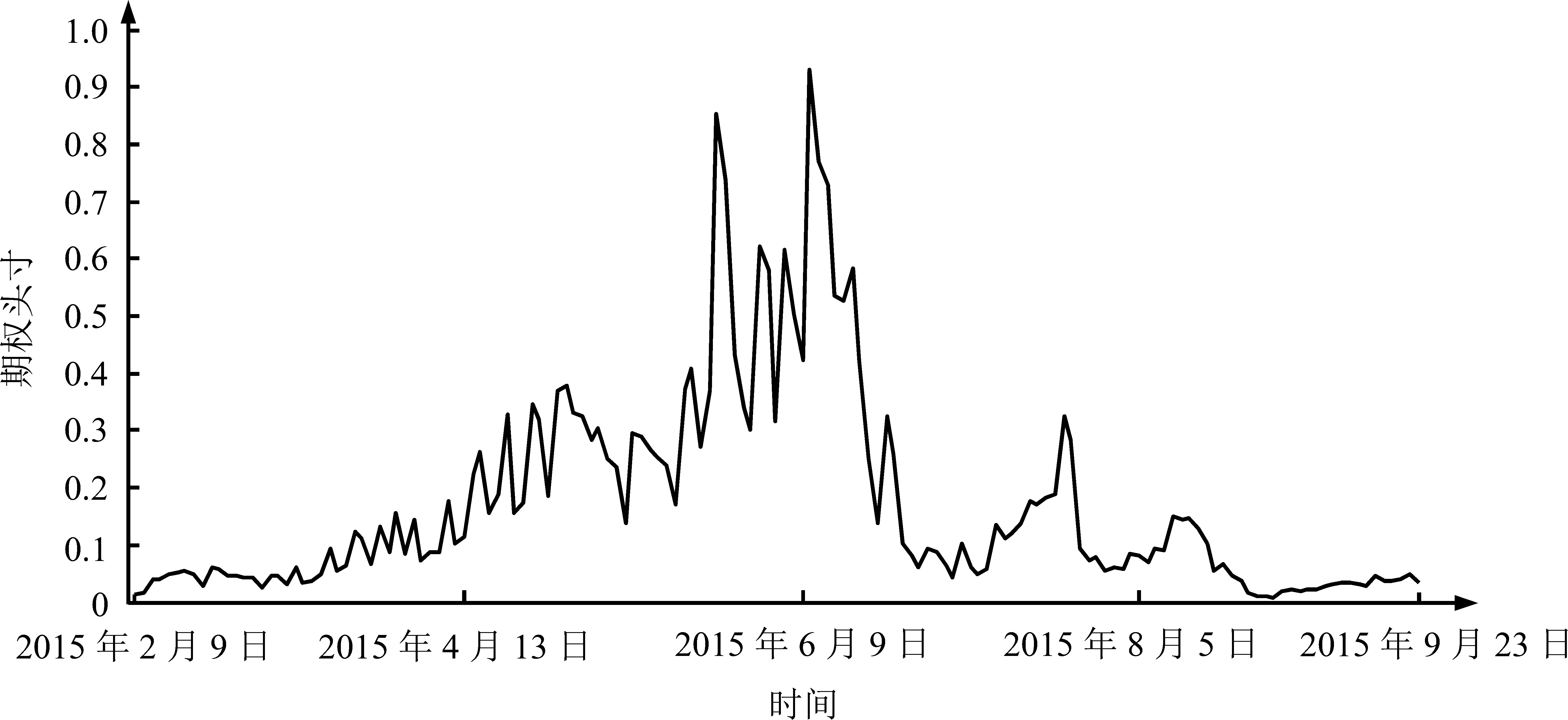
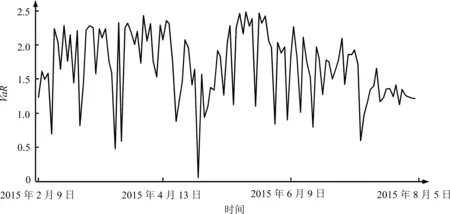
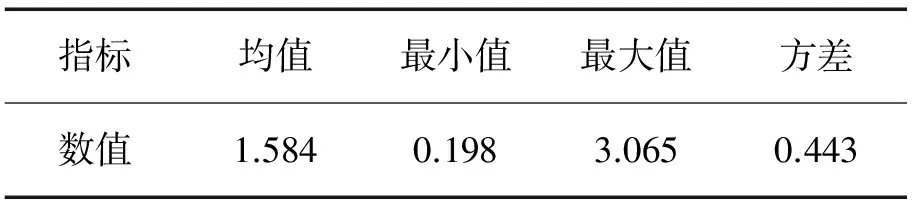
(16)式为本研究提出的调仓相机准则满足的等式，与不退出情形下套期保值组合的收益率(14)式本质上是一致的。由(16)式可得到每个时刻调仓与否的经济价值Πt，进而与调仓成本Ct进行比较。若Πt>Ct，则在t时刻选择调仓；若Πt

5 实证分析

5.1 基于VaR的期权动态套期保值分析

本研究实证数据来自万德数据库，选定上证50ETF标的及与之对应的一只看跌期权，期权代码为1000040(简称为期权40)，敲定价为2.400元，153天后到期(2015年9月23日到期)。假设投资者在2015年2月9日持有10 000份上证50ETF标的资产，当前价格是2.331元，他担心标的资产价格会持续下跌，决定买入看跌期权40对其进行套期保值。选取2011年1月4日至2015年2月6日的历史数据为样本数据，经分析发现标的资产价格服从几何布朗运动。然后，再选取2015年2月9日至2015年9月23日为实证研究时间区间。2015年9月23日标的资产价格为2.180元。在t个交易日，投资者根据市场和自身具体情况，制定购买期权的成本预算，并确定投资预期收益率。本研究假定现货头寸为1，那么当前标的资产的价值为St，投资者的成本预算和预期收益率都以St为参考，不同的投资者成本预算和预期收益率不同。本研究假定投资者愿意支付当前价值的0.35%购买期权，即成本预算为Qt，Qt=0.35%St；在期末时，投资者预期最低收益为Bt，Bt=(1+0.175%)St。取置信水平α=0.05。参考彭红枫等[30]的研究，取γ=1。采用GARCH模型一步滑动预测得到模型参数μt和σt。

通过求解模型(P1)得到期权40动态套期保值头寸，见图1，其描述性统计结果见表1。

表1 期权套期保值头寸描述性统计结果Table 1 Descriptive Statistics Results of Option Position with Hedging

图1 调整前期权套期保值头寸Figure 1 Option Position with Hedging before Adjusting

图2 调整前期权套期保值的VaRFigure 2 VaR Hedging with Option before Adjusting

由图1可知，在投资期间期权头寸调整幅度较大，而在投资期前后两段，大部分天数内期权头寸只是基于前一交易日微小调整。由表1可知，套期保值头寸随时间不断变化，均值为0.174，说明平均一单位的现货标的需要0.174单位期权40进行套期保值；套期保值头寸的方差为0.033，可以看出套期保值头寸变化比较剧烈。图2给出每个交易日期权套期保值的VaR。

为了定量表示套期保值风险，表2给出期权套期保值VaR的描述性统计结果。

表2 期权套期保值的VaR描述性统计结果Table 2 Descriptive Statistics Results of VaR Hedging with Option

由图2和表2可知，期权套期保值在控制VaR方面方差偏大，说明套期保值最大损失波动性较大。

以10 000份标的资产为例，通过求解(P1)模型最后得到2015年9月23日投资者持有期权40头寸338.060份，也就是338.060份标的以敲定价格2.400元交易，剩下9 661.940份标的以当前价格2.180元交易。本研究还考虑期权头寸变化带来的成本或收益，若相邻两个交易日期权头寸有所增加，表示要买入期权，需要支付期权金；若期权头寸有所减少，说明要卖出期权，获得收益。在投资期间买卖期权交易收入416.700元。因此，利用期权套期保值最后收益为

338.060×(2.400-2.180)+416.700=491.073元

标的资产的期初价格为2.331元。若不利用期权套期保值，标的资产价格从期初的2.331元降到2.180元，损失1 510元。基于以上分析可知，利用期权可以达到套期保值的目的。

5.2 退出相机决策分析

通过(13)式计算第t个交易日退出相机的经济价值Γt。若退出相机的经济价值为负，说明若要退出，投资者要求得到正的收益。每个投资者选择退出投资愿意付出的最大成本不同。本研究假设投资者最大退出成本为Dt=-3，即投资者要求正收益为3元时才会选择退出。因此，投资者通过比较Γt与Dt做出退出相机决策。若Γt>-3，则投资者可以选择在第t个交易日退出投资；若Γt<-3，则投资者在第t个交易日不退出投资。利用(13)式计算出每个交易日的经济价值，如通过计算得到前3个交易日的经济价值分别为-2.013、-2.018和-2.059，2015年5月26日和27日的经济价值为-3.232和-3.148。然后，比较经济价值与假设的最大退出成本-3的大小，得到7个退出交易日和退出收益，见表3。

表3 退出交易日及收益Table 3 Quit Trading Days and Returns

由表3可知，在以上7个交易日退出投资将获得比较大的利润，对于投资者而言，在这些交易日退出投资可以达到预期目的。这体现了期权套期保值的灵活性，以较小的代价为标的资产提供保护。

5.3 调仓相机决策分析

考虑每个投资交易日，套期保值者除了做出是否退出投资决策外，还将面临是否调仓的决策。若选择不调仓，维持上一交易日持有的期权头寸不变；若选择调仓，则通过买卖期权更新期权头寸。计算每个交易日调仓成本，由(16)式计算每个交易日调仓的经济价值。然后，比较调仓经济价值与调仓成本，决定是否调仓。为了对比分析考虑调仓相机决策的效果，将调仓前和调仓后的结果放一起进行比较，图3给出不考虑调仓相机和考虑调仓相机的期权套期保值头寸。

由图3可知，调整后期权头寸没有调整前期权头寸的调整频率高，大部分交易日都保持原头寸不变，减少了一些不必要的期权交易。

通过比较套期保值组合的在险价值VaR体现调仓与否和退出与否决策的优劣，下面对比研究选择调仓相机与否的VaR，表4给出做出调仓相机决策后套期保值风险VaR的描述性统计结果。

表4 调整后期权套期保值的VaR描述性统计结果Table 4 Descriptive Statistics Results of VaR Hedging with Option after Adjusting

图4给出调仓相机决策前后套期保值VaR的对比图。

图3 调整前后期权头寸对比Figure 3 Comparisons of Option Positions before and after Adjusting

图4 调整前后期权套期保值VaR的对比Figure 4 Comparison of VaR Hedging with Option before and after Adjusting

通过对比分析可知，调仓决策后的VaR比调仓决策前的小。因此，调仓决策后套期保值的绩效较好。根据模型(P1)和调仓相机决策可得1份标的资产对应的期权头寸，然后结合调仓相机准则确定更新头寸还是保持头寸不变，得到每个交易日期权持有头寸。通过计算与比较，得到最后一个交易日期权持有头寸为117.430份，即117.430份标的资产以敲定价格2.400卖出，剩下9 882.570份以当前价格2.180卖出。同时，通过期权本身交易收益3 232元。相对于期初，调整后投资者最后获得的总利润为

117.430×(2.400-2.180)+3 232=3 257.835元

这比调整前的利润多2 766.762元。调整后的套期保值策略获得的收益比调整前套期保值策略获得的收益更多，说明对于期权动态套期保值而言，最优的策略并不是每一个交易日都进行调仓，而只是需要在一部分的时间点进行动态调仓，剩下的时间点只需要维持上一个交易日的仓位即可。综上所述，本研究提出的动态调仓相机决策较无相机决策下的套期保值表现更好。

6 结论

本研究在传统的期权套期保值模型基础上进一步研究退出和调仓双相机抉择问题，在满足预算、预期收益、头寸约束条件下，建立期权套期保值组合VaR风险最小的动态套期保值模型。借助经济价值提出投资者在每个决策时刻是否退出投资准则和调仓与否准则，利用上证50ETF及所对应的看跌期权套期保值组合进行实证分析。研究结果表明，在退出相机决策中，给投资者提供了7个提前退出投资的交易日，在这些交易日若选择退出投资，可以规避后期价格可能下跌的风险。根据调仓相机决策准则,套期保值组合的VaR较没有调仓决策的情形小，且调整后减少了调仓成本，获得的收益比调整前套期保值策略获得的收益更多。这说明，对于期权动态套期保值而言，最优的策略并不是每一个交易日都进行调仓，而只需要在一部分时间点进行动态调仓，剩下的时间点只需要维持上一个交易日的仓位即可。在本研究中，退出相机抉择和调仓相机抉择的引入改进了传统的期权套期保值模型，为投资者提供了更有效的投资策略，也为期权动态套期保值提供了新的思路。

本研究是进一步优化传统期权套期保值头寸的一个尝试，尚存在一些不足。其中一个值得继续深入探讨的话题是风险测度函数的选择问题，本研究为简单起见选择VaR作为风险度量标准，未来研究可考虑其他一致性风险测度函数，如建立基于CVaR的期权套期保值双相机抉择模型。另外，在模型(P1)的约束条件中，本研究限定期权总头寸小于1，后续研究可以进一步推广到期权头寸大于1的情形。最后，也可能是比较难的一个尝试，就是建立合适的模型同时考虑VaR和经济价值两个因素。

[1]DARK J.Futures hedging with Markov switching vector error correction FIEGARCH and FIAPARCH.JournalofBanking&Finance,2015,61(2):S269-S285.

[2]ZHOU J.Hedging performance of REIT index futures:a comparison of alternative hedge ratio estimation methods.EconomicModelling,2016,52(B):690-698.

[3]谢赤,屈敏,王纲金.基于M-Copula-GJR-VaR模型的黄金市场最优套期保值比率研究.管理科学,2013,26(2):90-99.

XIE Chi,QU Min,WANG Gangjin.Research on optimal hedging ratios of gold market based on M-Copula-GJR-VaR model.JournalofManagementScience,2013,26(2):90-99.(in Chinese)

[4]孙艳,何建敏,周伟.基于UHF-EGARCH模型的股指期货市场实证研究.管理科学,2011,24(6):113-130.

SUN Yan,HE Jianmin,ZHOU Wei.Empirical research on the stock index market based on the UHF-EGARCH model.JournalofManagementScience,2011,24(6):113-130.(in Chinese)

[5]傅俊辉,张卫国,杜倩,等.规避逐日盯市风险的期货套期保值模型.管理科学,2011,24(3):86-93.

FU Junhui,ZHANG Weiguo,DU Qian,et al.Futures hedging models under mark-to-market risk.JournalofManagementScience,2011,24(3):86-93.(in Chinese)

[6]PARK T H,SWITZER L N.Bivariate GARCH estimation of the optimal hedge ratios for stock index futures:a note.TheJournalofFuturesMarkets,1995,15(1):61-67.

[7]WEI Y,WANG Y,HUANG D.A copula-multifractal volatility hedging model for CSI 300 index futures.PhysicaA:StatisticalMechanicsandItsApplications,2011,390(23/24):4260-4272.

[8]HOU Y,LI S.Hedging performance of Chinese stock index futures:an empirical analysis using wavelet analysis and flexible bivariate GARCH approaches.Pacific-BasinFinanceJournal,2013,24:109-131.

[9]SCHEUENSTUHL G,ZAGST R.Integrated portfolio management with options.EuropeanJournalofOperationalResearch,2008,185(3):1477-1500.

[10] WANG X T,ZHAO Z F,FANG X F.Option pricing and portfolio hedging under the mixed hedging strategy.PhysicaA:StatisticalMechanicsandItsApplications,2015,424:194-206.

[11] ARAI T.An extension of mean-variance hedging to the discontinuous case.FinanceandStochastics,2005,9(1):129-139.

[12] KALLSEN J,PAUWELS A.Variance-optimal hedging for time-changed Lévy processes.AppliedMathematicalFinance,2011,18(1):1-28.

[13] LIANG C,LI S.Option pricing and hedging in incomplete market driven by normal tempered stable process with stochastic volatility.JournalofMathematicalAnalysisandApplications,2015,423(1):701-719.

[14] WONG K P.Currency hedging with options and futures.EuropeanEconomicReview,2003,47(5):833-839.

[15] WONG K P.Production and hedging under state-dependent preferences.TheJournalofFuturesMarkets,2012,32(10):945-963.

[16] FRECHETTE D L.The demand for hedging with futures and options.TheJournalofFuturesMarkets,2001,21(8):693-712.

[17] TOPALOGLOU N,VLADIMIROU H,ZENIOS S A.Optimizing international portfolios with options and forwards.JournalofBankingandFinance,2011,35(12):3188-3201.

[18] BAJO E,BARBI M,ROMAGNOLI S.A generalized approach to optimal hedging with option contracts.TheEuropeanJournalofFinance,2015,21(9):714-733.

[19] LIEN D,TSE Y K.Hedging downside risk:futures vs.options.InternationalReviewofEconomics&Finance,2001,10(2):159-169.

[20] BAJO E,BARBI M,ROMAGNOLI S.Optimal corporate hedging using options with basis and production risk.TheNorthAmericanJournalofEconomicsandFinance,2014,30:56-71.

[21] 杨春鹏.限定亏损概率下期权交易中的套期保值比率研究.预测,2000,19(3):61-62.

YANG Chunpeng.The hedge ratio for option trade under limited loss probability.Forecasting,2000,19(3):61-62.(in Chinese)

[22] 尹力博,韩立岩.人民币外汇期权套保策略:基于随机规划模型.管理科学学报,2012,15(11):31-44.

YIN Libo,HAN Liyan.The hedging value and strategy of RMB foreign currency options:from the perspective of stochastic programming.JournalofManagementScienceinChina,2012,15(11):31-44.(in Chinese)

[23] MELNIKOV A,SMIRNOV I.Dynamic hedging of conditional value-at-risk.Insurance:MathematicsandEconomics,2012,51(1):182-190.

[24] CAPINSKI M J.Hedging conditional value at risk with options.EuropeanJournalofOperationalResearch,2015,242(2):688-691.

[25] 孙燕红,费广平.VaR最小化的股指期货套期保值比率研究.数理统计与管理,2015,34(4):750-760.

SUN Yanhong,FEI Guangping.Study on mini-VaR hedging with stock index futures.JournalofAppliedStatisticsandManagement,2015,34(4):750-760.(in Chinese)

[26] LIU N,LAI Y S.Aconditionalmeasureforfutureshedgingperformance.Taiwan:National Chiao Tung University,2012.

[27] LENCE S H.The economic value of minimum-variance hedges.AmericanJournalofAgriculturalEconomics,1995,77(2):353-364.

[28] FLEMING J,KIRBY C,OSTDIEK B.The economic value of volatility timing.TheJournalofFinance,2001,56(1):329-352.

[29] NOLTE I,XU Q.The economic value of volatility timing with realized jumps.JournalofEmpiricalFinance,2015,34:45-59.

[30] 彭红枫,陈奕.套期保值中动态调仓的相机抉择.中国管理科学,2013,21(S1):321-327.

PENG Hongfeng,CHEN Yi.Discretion in dynamical positions adjustment of hedging.ChineseJournalofManagementScience,2013,21(S1):321-327.(in Chinese)

[31] AHN D H,BOUDOUKH J,RICHARDSON M,et al.Optimal risk management using options.TheJournalofFinance,1999,54(1):359-375.

DualDiscretionModelofDynamicHedgingwithOption:AnEmpiricalStudy

YU Xing，ZHANG Weiguo，LIU Yongjun

School of Business Administration, South China University of Technology, Guangzhou 510640, China

Since the financial market has the nature of variability, investors should always dynamically adjust their hedging strategy accordingly so as to make sure the risk of portfolio price fluctuation can be hedged. Yet as the traditional static hedging with option will not meet this requirement, it is desirable to establish dynamic hedging with option model to obtain the optimal dynamic option positions. Therefore, investors should dynamically make relocation by referring to the positions generated by the established model in order to minimize the risk. However, investors should pay premium to call option and hedging, namely investors must bear the cost when they want to minimize the risk. In this case, the investors will face one problem that whether the investment is cost-effective or not. Moreover, to buy European long put option will mitigate the risk of spot price dropping. European style option can only be exercised at the expiry date. Investors will not have to hold the option until the expiry date. Then another problem for investors is how to select the most profitable timing to exit the investment.

This paper puts forward the criteria of exiting investment and making adjustment to the existing problems caused the traditional strategy hedging with option such as missing the best opportunity to exit investment or too frequent relocation makings. It further optimizes the traditional strategy of hedging with option. The optimal dynamic hedging model is established on the basis of VaR (value at risk) by fulfilling the conditions of enough budgets, anticipated profit and good positions. Traditional dynamic hedging strategy is formed. Hence, the risk and cost will be uniformly measured based on economic value of risk. Furthermore, the strategy of hedging with option will be adjusted accordingly under the dual discretion criterion of exiting investment and relocation by using end-term performance evaluation. How to select the timing to exit investment during investment period will be another problem for dynamic hedging with option.

The result shows that the cease of discretion rules will provide the reference timing to exit investment. Discretion criterion of relocation will decrease the cost of relocation by reducing the unnecessary relocation makings. Defects caused by the traditional dynamic hedging with option strategy are explored by comparisons. Hedging with option based on dual discretion is proved to be more effective. 7 proposed reference timings to exit investment makes a higher profit and the profit is increased when discretion criterion is applied.

Optimal hedging model which takes dual-discretion into consideration improved the single-discretion in traditional model. It proposes a more effective strategy in risk control. More importantly, it has more significance in practice when investors are making their decisions.

dynamic option hedging；cease of discretion rules；discretion rules of relocation；value at risk；economic value

Date:March 15th, 2016

DateJune 24th, 2016

FundedProject:Supported by the National Natural Science Foundation of China(71501076), the Natural Science Fund of Guangdong (2014A030310454 ) and Financial Service Innovation and Risk Management Research Base of Guangzhou

Biography:YU Xing is a Ph.D candidate in the School of Business Administration at South China University of Technology. Her research interests cover financial engineering and risk management. E-mail：bmyuxing2015@mail.scut.edu.cn

ZHANG Weiguo, doctor in management, is a professor in the School of Business Administration at South China University of Technology. His research interests include decision analysis, information processing, artificial intelligence and portfolio managements. He is the principal investigator of the project titled “Evolution and controlling of the complex financial system research”, funded by the National Social Sciences Foundation of China(70573030). E-mail: wgzhang@scut.edu.cn

LIU Yongjun, doctor in management, is a professor in the School of Business Administration at South China University of Technology. His research interests include mathematical finance, financial engineering and investment decision. His representative paper titled “A multi-period fuzzy portfolio optimization model with minimum transaction lots” was published in theEuropeanJournalofOperationalResearch(Issue 3, 2015). E-mail: bmyjliu@scut.edu.cn

F830.9

A

10.3969/j.issn.1672-0334.2016.04.012

1672-0334(2016)04-0139-10

2016-03-15修返日期2016-06-24

国家自然科学基金(71501076)；广东省自然科学基金(2014A030310454)；广州市金融服务创新与风险管理研究基地

余星，华南理工大学工商管理学院博士研究生，研究方向为金融工程和风险管理等，E-mail：bmyuxing2015@mail.scut.edu.cn

张卫国，管理学博士，华南理工大学工商管理学院教授，研究方向为决策分析、信息处理、人工智能和投资组合管理等，主持国家社会科学基金重大项目“金融复杂系统的演化与控制研究”(11&ZD156)，E-mail：wgzhang@scut.edu.cn

刘勇军，管理学博士，华南理工大学工商管理学院教授，研究方向为数理金融、金融工程和投资决策等，代表性学术成果为“A multi-period fuzzy portfolio optimization model with minimum transaction lots”，发表在2015年第3期《European Journal of Operational Research》，E-mail：bmyjliu@scut.edu.cn

□