特征值在高等代数中的作用

杨闻起

（宝鸡文理学院 数学与信息科学学院，陕西 宝鸡 721013）

特征值在高等代数中的作用

杨闻起

（宝鸡文理学院 数学与信息科学学院，陕西 宝鸡 721013）

以高等代数中的定义、定理和例题为依据，论述了特征值具有化繁为简的作用，它还是实对称矩阵和二次型的本质所在.特别地，它是解决许多代数问题的重要工具.

特征值；特征向量；矩阵；二次型；线性变换

特征值作为高等代数中的基本概念，在矩阵、二次型和线性变换中起着十分重要的作用，而且为解决一些代数问题提供了很好的方法［1-8］.

1 特征值具有化繁为简的作用

定义1［1］278设A是数域P上的n阶矩阵，λ∈P，如果存在数域P上的n维非零列向量α，使得Aα= λα，则称λ为A的一个特征值，α为A的属于λ的特征向量.设σ是线性空间V上的线性变换，λ∈P，如果存在V中的n维非零列向量α，使得σα=λα，则称λ为σ的一个特征值，α为σ的属于λ的特征向量.

从定义1可以看出，特征值可以把矩阵与向量的乘法简化为数与向量的数乘，也可把向量在线性变换之下的像简化为数与向量的数乘，这种化复杂运算为简单运算的特点注定了特征值具有化繁为简的作用.

定理1表明，在相似关系下，实对称矩阵A都可以化简对角型矩阵，而该对角型矩阵完全由A的特征值决定.

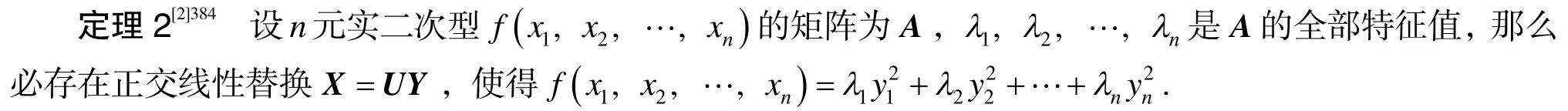
定理2表明，只要给出实二次型的矩阵的特征值，那么该二次型就可以化简为标准型.

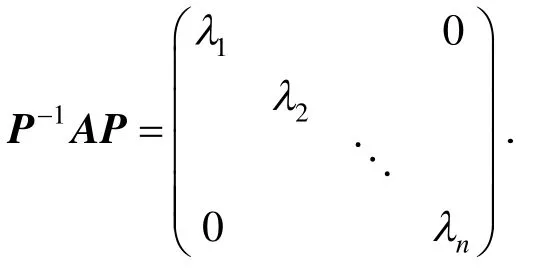
定理3表明，在相似关系下，只要已知矩阵A的特征值及n个线性无关的特征向量，那么，A就可以化简为对角型矩阵.

定理4［2］299设σ是n维线性空间V上的线性变换，λ1, λ2, L, λn是σ的全部特征值，并且σ有n个线性无关的特征向量，那么存在V的一组基，使得σ关于该基的矩阵为对角型.

定理4表明，只要已知线性变换的全部特征值及n个线性无关的特征向量，那么，该线性变换就可以对角化.

定理5表明，在相似关系下，任意n阶矩阵可化简为Jordan标准型，且Jordan标准型与特征值有紧密联系.

综上可见，不论从特征值的定义还是性质来看，特征值均起到了化繁为简的作用.

2 特征值是对称矩阵和二次型的本质所在

定理1说明，特征值相同的实对称矩阵是相似的，所以在相似关系下，实对称矩阵由它的特征值决定，也就是说，特征值是实对称矩阵的本质所在.

定理2说明，只要已知实二次型的矩阵的特征值，那么，就可把二次型化为标准型，还可进一步确定出二次型的正定性、正负惯性指数和符号差等，所以，特征值也是实二次型的本质所在.

有些矩阵，只要已知它的特征值和个别特征向量，就可以完全决定这个矩阵.

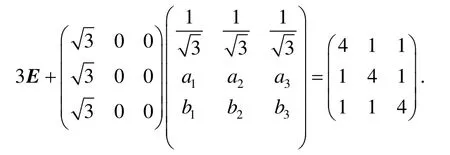
3 特征值是解决代数问题的重要工具

高等代数中的许多问题，表面看无从下手，难以证明，但是，从特征值的角度来分析，却很容易得到解决.

例2 设A是三阶实对称矩阵，A2=E，且rank(A-E)=1，求行列式的值.

分析 例2表面看似乎无从入手，但是只要注意到，利用已知条件可以求得A的特征值，就不难解决问题.

例3 设A是n阶正定矩阵，S是n阶反对称矩阵，证明：

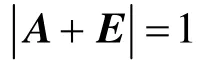
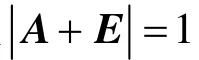
例3和例4均是关于行列式值的问题，其中的已知条件与要证明的结果之间似乎逻辑上没有直接联系，给人无从下手的感觉.但是，由于矩阵的特征值等于它的所有特征值的乘积，因此，可借助特征值寻找解题思路.

例5 实数域上的n维线性空间V上任一线性变换σ必有一维或二维不变子空间.

［1］ 张禾瑞.高等代数［M］.北京：高等教育出版社，1990

［2］ 北京大学数学系.高等代数［M］.北京：高等教育出版社，2003

［3］ 徐仲，张凯院，陆全，等.矩阵论简明教程［M］.北京：科学出版社，2008

［4］ 张红玉.矩阵特征值的理论及应用［J］.山西大同大学学报：自然科学版，2009，25（1）：15-16

［5］ 王莲花.矩阵AB与BA的特征值问题及其应用［J］.大学数学，2007，23（1）：135-139

［6］ 杨闻起.高等代数方法研究［M］.西安：西安出版社，2009

［7］ 赵天绪，杨闻起.线性代数［M］.西安：陕西科技出版社，2014

［8］ 杨闻起.论线性代数的应用型教学方法［J］.宝鸡文理学院学报：自然科学版，2015，35（1）：78-80

The function of characteristic value in higher algebra

YANG Wen-qi
（School of Mathematics and Informatics，Baoji University of Arts and Sciences，Baoji 721013，China）

On the basis of definitions，theorems and examples in higher algebra，the simplified role of eigenvalues is discussed.Besides，the fact that the essence of real symmetric matrix and quadratic form can be reflected by eigenvalues is showed.In particular，pointed out that the eigenvalues is the important toole for solving many problems of algebra.

characteristic value；characteristic vector；matrix；quadratic form；linear transformation

O151.2∶G642.0

A

10.3969/j.issn.1007-9831.2016.06.020

1007-9831（2016）06-0064-03

2016-03-30

宝鸡文理学院第十一批教学改革研究项目（JGYB15013）

杨闻起（1962-），男，陕西岐山人，教授，从事代数学研究.E-mail：baojiywq@126.com