STFT和小波分析在电压暂降检测中的应用

徐 健，张 瑾，李彦斌

（西安工程大学 电信学院，陕西 西安710048）

STFT和小波分析在电压暂降检测中的应用

徐 健，张 瑾，李彦斌

（西安工程大学 电信学院，陕西 西安710048）

对于电压暂降特征测量幅值，持续时间的准确检测是电压质量评估与抑制干扰首要解决的重要课题。本文提出基于对STFT基频幅值曲线增加阈值的新方法。分别用STFT（短时傅里叶变换），小波变换作为时频信号分析工具，针对电压暂降扰动检测问题进行对比研究。电压暂降在起始和结束时刻会产生高频信号，通过检测高频信号发生时刻来定位扰动。使用该方法可在基频幅值曲线图中直观清楚地看出扰动起始和结束时间。并对该方法的抗噪情况进行了研究。仿真结果证明，本文所提出的方法能够准确的定位电压暂降扰动，抗噪能力强，用其来检测电压暂降是一种可行有效的检测方法。

电压暂降；STFT；小波变换；时频信号分析

20世纪80年代以来，随着现代电力系统的负荷构成变化，使电能质量问题日益突出。暂态电能质量问题因其发生的频繁性、随机性以及对敏感设备的严重危害性而备受关注，成为电能质量分析的研究重点。电压暂降是一种常见的暂态扰动，其发生次数频繁，影响范围大，损坏敏感设备，对用户造成的损失和危害是十分严重的[1]。目前，对电压暂降扰动特征量提取常用的方法有小波变换，dq变换，HHT变换和瞬时无功功率理论等。

文中重点研究STFT和小波变换方法两种方法，分别对电压暂降进行仿真分析，并将仿真结果对比，提出用改进的STFT基频幅值曲线对电压暂降信号进行定位。

1 短时傅里叶变换

1946年Gabor利用快速傅里叶变换加窗函数，提出了短时傅立叶变换，即将不平稳信号的过程看成是一系列短时平稳过程的集合。短时傅里叶变换可利用快速傅里叶变换实现快速计算，扰动信号经短时傅里叶变换后即可得到时域最大幅值，并准确反映出扰动发生的时刻和持续时间[2-6]。

学术思想是：选择一个时频局部化的窗函数，窗函数可为hanning窗，hamming窗，高斯窗，blackman窗等。窗函数g（t）在一个短时间间隔内是平稳的，移动窗函数，使原始信号h（t）与g（t）在不同的有限时间宽度内是平稳信号。对于原始信号可以先乘以所选定的窗函数，该窗函数仅在一段时间不为零，将两者的乘积再进行一维的傅里叶变换[7-8]。最后，将这个窗函数沿着时间轴挪移，所得到一系列的傅里叶变换结果排开则成为二维表象[9]。数学上，这样的操作可写为：

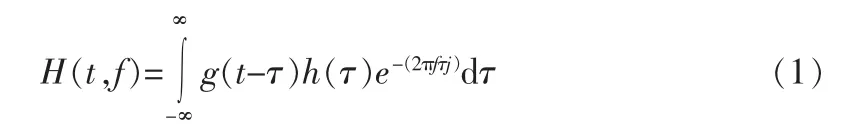
其中，f是频率，t是时间，随着时间t的改变，窗函数g（t-τ）在时间轴上会有位移，得到短时傅里叶变换的结果H（t，f）。由以上分析得到，一旦窗函数选定，其形状就会固定不变，相应地频率分辨率也就确定了。短时傅里叶变换相当于用每一段函数在窗函数上的投影，这样减少了每段的频谱泄露，提高了频谱曲线的分辨率[10-11]。

2 小波变换

若函数ψ（x）满足，

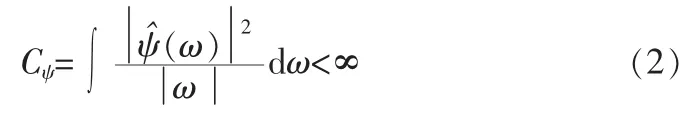
则连续小波变换定义为

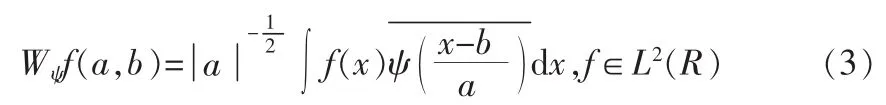
即f（x）是以ψ（x）为基的连续小波变换，由式（3）可看出，连续小波变换Wψf（a，b）是f（x）在函数ψa，b（x）上的投影。它将一个一维函数f（x）变换为一个二维函数。其中，a称为尺度因子，b称为平移量[12-14]。

3 仿真分析

文中采用MATLAB仿真软件，以表1的条件为基础，对电压暂降信号进行了短时傅里叶变换和小波变换实验仿真。

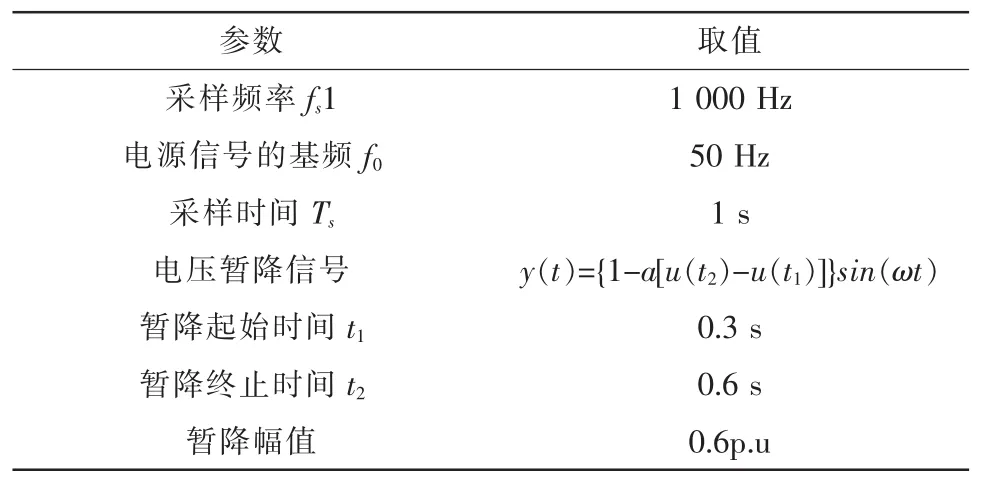
表1 仿真模型参数设置

图1是暂降扰动信号y（t）的Matlab仿真图。

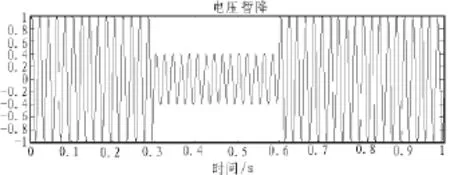
图1 电压暂降信号

3.1 电压暂降扰动定位

利用短时傅里叶变换对电压暂降信号进行分析。取80点的Hamming窗作为窗函数，可得基频幅值曲线如图2和时频等值曲线图3。从图2中可知，仿真结果显示暂降为0.6p.u。误差为0。从图3中可知，暂降的起始时间为0.302 5 s，结束时刻为0.602 5 s。误差为0.83%。

电压暂降产生和恢复的时刻会产生高频分量，可通过检测高频发生的位置来确定暂降的起始，结束时刻[14]。用DB6小波分析，对信号进行3尺度分解得到近似信号部分和高频信号部分，分别如图4所示。

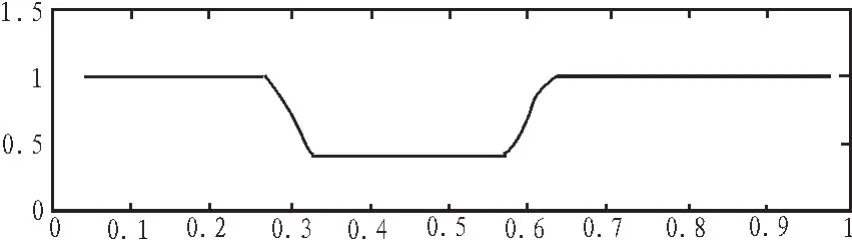
图2 基频幅值曲线

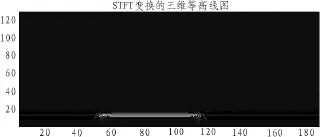
图3 时频等值曲线

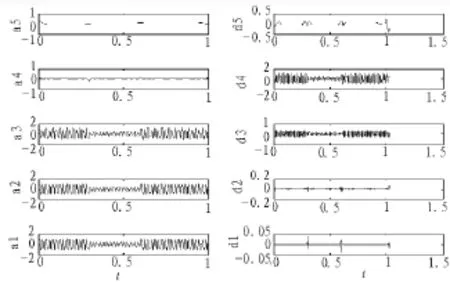
图4 小波分解后的各层逼近信号和细节信号

可见，小波变换系数d3完全不能确定暂降，系数d2模极大值不能够清楚地定位扰动，而系数d1模极大值与前两者相比，可准确定位扰动即起始时刻为0.3 s，结束时刻为0.6 s，误差为0。

图2，图3均可确定电压暂降扰动的起止时刻，仿真结果显示小波变换较短时傅里叶变换更为准确，但小波变换不能直接检测幅值，这也是其应用于电压暂降扰动检测的局限性。

为了提高短时傅里叶变换检测的准确性，本论文对其基频幅值曲线进行改进。通过设置阈值来增强电压暂降的扰动特征，使得在基频幅值曲线中电压降落明显，可清楚的观察到暂降的起止时刻和降落幅值。本论文阈值取0.71，如图5所示。由图可见，暂降期间幅值为0.4，起始时刻为0.3 s，终止时刻为0.6 s，与实际值一致，误差为0。因此，改进后的基频幅值曲线可精确的检测电压暂降前后的幅值及暂降所持续的时间。

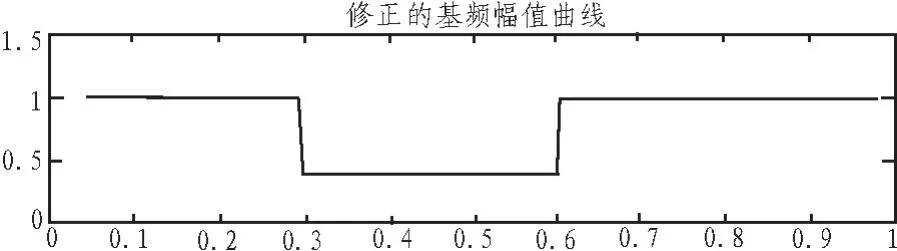
图5 改进的基频幅值曲线

3.2 含噪声的电压暂降扰动定位

在仿真信号中加入信噪比为50 dB的高斯白噪声，电压暂降信号为图6。用STFT，DB6小波和改进的STFT分别对含噪声信号进行扰动定位测试，所得结果如图7～9。

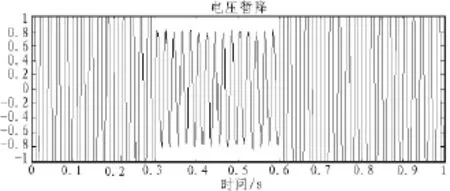
图6 含噪声的电压暂降信号

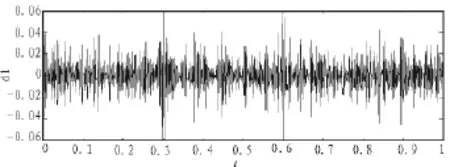
图8 小波变换系数d1

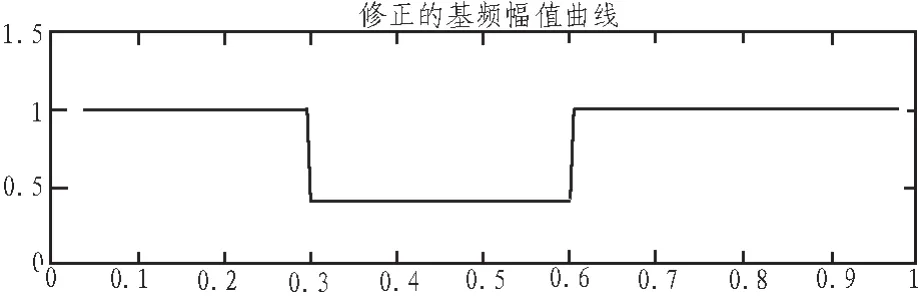
图9 改进的STFT基频幅值曲线

由图7、8可见，未改进的短时傅里叶变化的基频幅值曲线出现波动，不能清楚地反应暂降幅值。图8中小波变换系数d1的模极大值不够清晰，定位能力变弱。对含噪声的扰动信号分析结果表明前两种方法均受到噪声影响，使得检测结果不够准确，抗干扰能力弱。图9为改进的基频幅值曲线，加入的扰动信号并没有造成基频幅值曲线的波动，仍能清楚地定位暂降起止时刻，即起始时刻为0.3 s，结束时刻为0.6 s。暂降幅值为0.6p.u。由此可看出改进后的STFT基频幅值曲线抗干扰能力较强，检测结果准确。

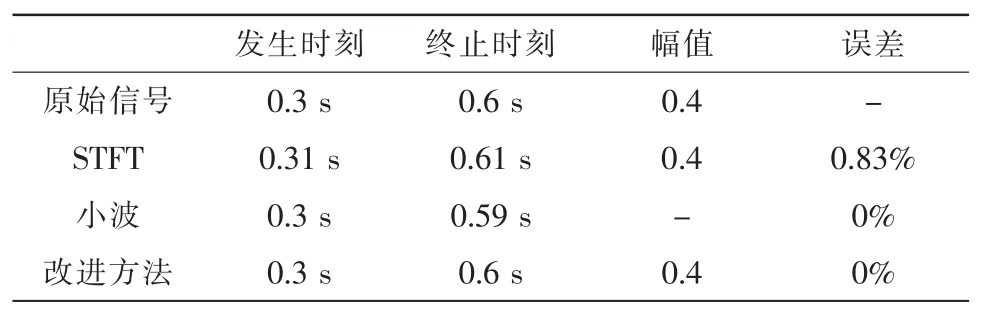
表2 仿真结果对比

4 结 论

文中提出了两种电压暂降扰动定位的检测算法，通过仿真比较，得出以下结论：

1）采用STFT对电压暂降信号进行分析得到时频等值曲线可检测暂降的起止时刻，存在0.83%的误差。所得的基频幅值曲线可以准确检测出幅值，误差为0。用小波变换进行3尺度分析，得到的小波系数d1模极大值可清楚地判断起止时刻，但小波无法直接的检测出暂降的幅值。对基频幅值曲线加入阈值，使得暂降特征明显，可清晰地从图中检测出暂降起止时刻和幅值，误差均为0，具有较高的准确性。因此，在检测电压暂降特征值方面，改进的STFT基频幅值曲线更直观，更准确。

2）在对含噪声的电压暂降信号进行仿真分析发现，小波变换和短时傅里叶变换对信号的分析结果都有受到噪声的影响，而加了阈值的STFT基频幅值曲线则有很好的抗干扰能力。由以上结论可知改进的STFT基频幅值曲线在电压暂降中的优势，其对电能质量问题的解决治理具有重要的经济意义。参考文献：

[1]周林，吴红春，孟婧，等.电压暂降分析方法研究[J].高电压技术，2008，34（5）:1010-1016.

[2]潘朝洪，张昱，金心宇.加窗傅里叶和小波变换在电能质量分析中的综合应用[J].江南大学学报:自然科学版，2007，6（4）：403-408.

[3]董其国.电能质量技术问答[M].北京：中国电力出版社，2003.

[4]肖湘宁.电能质量分析与控制[M].北京：中国电力出版社，2004.

[5]卫俊平.时频分析技术及应用[D].西安电子科技大学，2005.

[6]杨志华，杨力华，译.小波基础及应用教程[M].北京:机械工业出版社，2006.

[7]徐健，张语勍，李彦斌，等.短时傅立叶变换和S变换用于检测电压暂降的对比研究[J].电力系统保护与控制，2014，42（24）:3-6.

[8]赵凤展，杨仁刚.基于短时傅里叶变换的电压暂降扰动检测[J].中国电机工程学报2007，27（10）:28-34.

[9]Stockwell R G，Mansinha L，Lowe R P.Localization of the complex spectrum:the S transform [J].Signal Processing，IEEE Transactions on，1996，44（4）:998-1001.

[10]赵凤展，杨仁刚.基于短时傅里叶变换的电压暂降扰动检测[J].中国电机工程学报2007，27（10）:28-34.

[11]肖湘宁，徐永海，刘吴.电压凹陷特征量检测算法研究[J]，电力自动化设备，2002，22（1）:19-22.

[12]郝晓平，党幼云 .基于FPGA的信号奇异性检测[J].西安工程大学学报，2011（6）:1-2.

[13]YuHua，Math H.J.Bollen.Time-Frequency and Time-Scale Domain Analysis of Voltage Disturbances [C].IEEE Transsactions on power delivery，2000（15）：1279-1283.

[15]张勇，管声启.基于小波提升分解的带钢表面缺陷检测[J].西安工程大学学报，2013（4）:1-2.

A wavelet transform and STFT are proposed in the application of voltage sag detection

XU Jian，ZHANG Jin，LI Yan-bin
（College of Electrics and Information，Xi’an Polytechnic University，Xi’an 710000，China）

In order to detect voltage sag characteristic quantity，such as amplitude and duration exactly，it is a important issue for voltage quality evaluation and disturbances suppression shuld be solved firstly.This paper proposes a new method to add a threshold value to fundamental frequency amplitude curve transformed by STFT.Using either STFT（Short-Time Fourier Transform）or wavelet transform as a time-frequency analysis tool for voltage sag detection comparative study.Voltage sags show high-frequency transients at sag initiation and at voltage recovery，we can detect the occurrence time to locate the disturbance of high frequency signal.This method detect the time at sag initiation and at voltage recovery.And I did a research about anti-noise ability.The simulation results show that the improved fundamental frequency amplitude curve can locate voltage sag disturbance exactly and have anti-noise ability，using this method to detect voltage sag is a feasible and effective.

voltage sag；STFT；wavelet transform；time-frequency analysis

TN99

A

1674－6236（2016）24-0085-03

2016-03-09 稿件编号：201603109

陕西省科技厅工业科技攻关项目（2015GY075）

徐 健（1963—），男，陕西西安人，硕士，副教授。研究方向：电能质量检测、信号与系统等。