基于伪随机序列的维纳滤波反卷积算法的改进
甄晓丹,郝凯学,李 梅
(中国地质大学(北京)信息工程学院,北京100083)
基于伪随机序列的维纳滤波反卷积算法的改进
甄晓丹,郝凯学,李 梅
(中国地质大学(北京)信息工程学院,北京100083)
应用于相关辨识中的维纳滤波反卷积算法对噪声的适应性不理想,辨识效果不佳。据此分析了维纳滤波反卷积算法在对大地辨识的过程中对噪声适应性不理想的原因,并提出了相应的改进算法:根据检测系统冲激响应的频谱范围,首先用常数进行处理,但实验效果不佳;再次改进后用可变函数代替不同阈值来调整算法,对带通内部分和带通外部分使用不同的估计方法,从而提高算法对噪声的适应能力。试验表明改进后的维纳滤波反卷积算法有较强的噪声适应能力,在相关辨识的应用中取得了良好的辨识效果。
相关辨识;维纳滤波反卷积算法;m序列;噪声
在相关辨识中,利用维纳滤波反卷积算法可以改善传统频域反卷积算法中的零点问题[1],还可以抑制掉部分噪声干扰,从而提高辨识效果[2]。但是,由于检测系统的系统函数带宽有限,频带外的噪声起伏会直接影响反卷积的效果,造成算法本身的稳定性较差;同时系统冲激响应和噪声的功率谱的倒数比往往取一个常数,而反卷积的结果对常数的取值非常敏感,反卷积后波峰较宽,辨识效果提高不明显[3]。通过使用不同的K值,对维纳滤波反卷积算法进行改进。对原算法和改进算法实验,仿真结果并不明显,随后,本文采用了另一种改进算法[4]:用可变函数代替不同阈值来调整系统冲激响应和噪声的功率谱的倒数比,对带通内部分进行AR模型拟合建模,对带通外部分进行插补估计。对比仿真后的时域辨识效果图可以发现用可变函数改进的维纳滤波算法可以得到更好的辨识效果。
1 方 法
1.1 基于m序列的相关辨识传输模型
在相关辨识中,可以认为检测系统的传输模型[5]是:发射设备向二阶系统(模拟大地这一复杂系统)发出m序列,m序列在二阶系统中传输,加入噪声干扰,由接收设备接收并采集输出。如图1所示(图中x(n)为m序列):
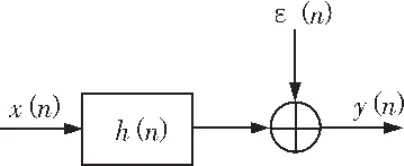
图1 相关辨识中伪随机信号传输模型示意图
m序列是一种常见的伪随机编码序列,是由带线性反馈的移位寄存器产生的一种周期最长的序列。它具有类似随机噪声的自相关特性,同时又具有周期性,因此容易产生和复制[6]。由于具有这些特点,m序列在信号处理方面获得了广泛的应用。
m序列的功率谱密度:
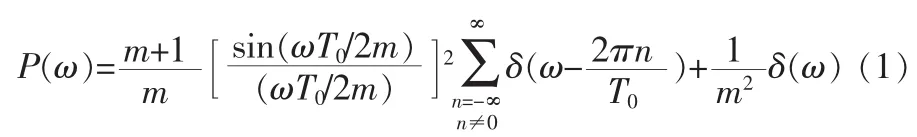
式(1)中,T0→∞和m/T0→∞时,m序列的功率谱密度特性趋于白噪声的功率谱密度特性。
1.2 维纳滤波反卷积
维纳滤波器用于反卷积系统辨识的示意图如图2所示。
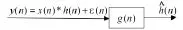
图2 维纳滤波器g(n)用于反卷积系统辨识的示意图
经过滤波器的系统输出为:
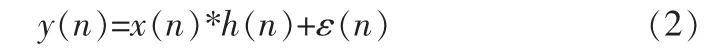
对式(2)等号两边做傅里叶变换,得到:
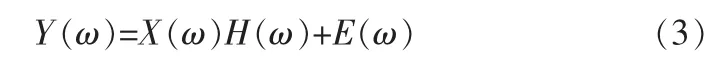
相除后得到:
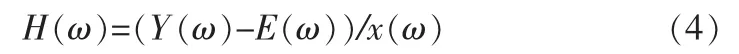
虽然H(ω)不一定有真正为零值的谱零点,但在这些点上的幅值可能很小时,这些微小值就会造成H(ω)值的较大变动,变换到时域会反演出的系统冲激响应失真[7]。所以我们考虑使用维纳滤波反卷积算法来解决这样的问题[8]。
假设一个滤波器g(n),能够满足用y(n)作为输入,输出

并且根据线性均方估计中的正交原理,必须保证:
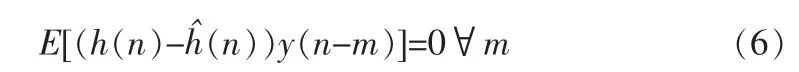
假设信号都是广义平稳,对式(5)等号两边进行相关运算后,再对等号两边做离散傅里叶变换,经过推导,得到维纳滤波器的表达式[9],由此我们得到的系统冲激响应的频域表达式
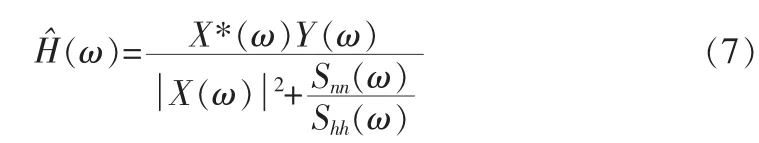
系统冲激响应和噪声的功率谱的倒数比用正常数γ代替,数量级需要根据经验来取,一般仿真经验,此时取0.01能保证基本的辨识效果。
由于检测系统的系统函数带宽有限,频带外的噪声起伏会直接影响反卷积的效果,造成算法本身的稳定性较差;同时系统冲激响应和噪声的功率谱的倒数比γ往往取一个常数,而反卷积的结果对常数的取值非常敏感[10],反卷积后波峰较宽,导致辨识效果提高不明显。通过修改系统冲激响应和噪声功率谱的倒数比γ对维纳滤波器进行改进,来进一步提高反卷积精确度。
1.3 改进的维纳滤波反卷积算法
1.3.1 修改系统冲激响应和噪声功率谱的倒数比对维纳滤波器进行改进
我们通过维纳滤波反卷积算法得到的系统冲激响应的频域表达式(7),我们考虑将Snn(ω)/Shh(ω)用(K|Hmax|)2来代替,得到:
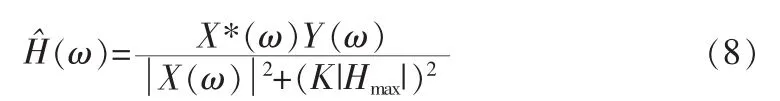
其中K为噪声压缩因子,用于在去卷积处理中控制噪声的压缩[11]。为了揭示K值对去卷积的影响,针对不同的K值进行试验,分别取K=0.02,0.1,0.5,1去卷积处理后的结果。
1.3.2 用可变函数改进系统冲激响应和噪声功率谱的倒数比γ
根据Snn(ω)/Shh(ω)与频带有关的分析,可以认为γ是一个随频率变化的函数[12],为了适应噪声的影响,取k为与|X(ω)|变化趋势相反的函数:
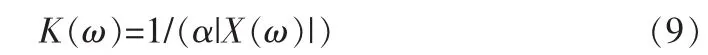
α作为一个乘数因子,用来匹配整个周期内Snn(ω)/Shh(ω)的变化。
则实际滤波公式为:
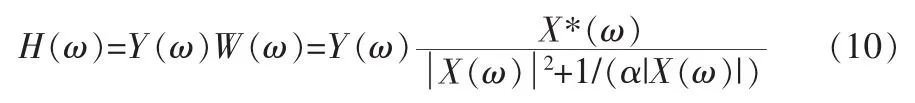
根据上述滤波公式,我们提出改进方法:当|X(ω)|小于某一阈值时,给W(ω)乘以一个是函数,来减小噪声响应。值得注意的是,缩小因子的选择要依据实际测量的大地系统来确定。
2 实验与结果
基于MATLAB对典型二阶系统来做大地系统辨识的仿真,给定一个待测的二阶系统,系统冲激响应为:
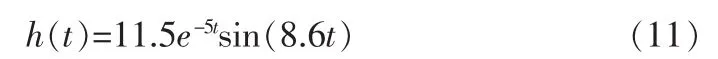
输入周期数是1,幅值为1 V,阶数为14的m序列,系统函数的采样间隔是0.001 s,时长7 s,加入5 V随机噪声,使用传统频域反卷积算法的仿真结果如图3所示。
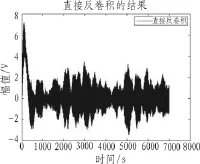
图3 传统频域反卷积算法的仿真结果
由式(8),使用不同的 K值进行试验,分别取 K=0.02,0.1,0.5,1,结果如图4所示。
从图中可看出,K值较小时有较好的去卷积效果,但引入的噪声大;K值较大时引入的噪声小,但反卷积效果很不理想;所以用可变函数改进系统冲激响应和噪声功率谱的倒数比,由公式(9)的函数,令α=1.8,对比维纳滤波反卷积算法与用可变函数改进的维纳滤波反卷积算法的仿真结果,如图5所示。
通过维纳滤波反卷积算法与改进的维纳滤波反卷积算法的两个时域辨识效果图的对比,可以看出改进的维纳滤波反卷积算法的辨识效果优于维纳滤波反卷积算法,而且就相关辨识的精确度来说,改进的维纳滤波反卷积算法的精确度优于维纳滤波反卷积算法,对噪声有较为明显的抑制作用。
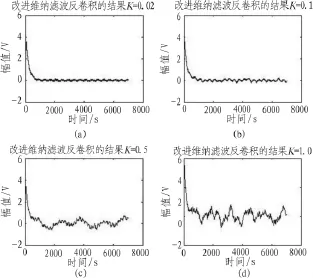
图4 使用不同K值改进的维纳滤波反卷积
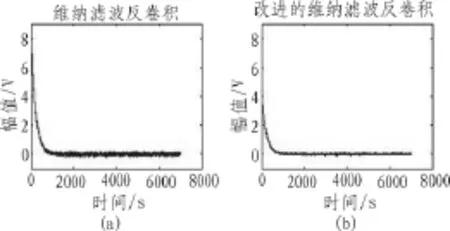
图5 两种算法对比结果
3 结束语
将Snn(ω)/Shh(ω)用(K|Hmax|)2来代替对维纳滤波反卷积算法进行改进,可以发现,对K值的取值不同,辨识效果存在较大的差异:小K值的反卷积效果较好,但相对引入的噪声较大;大K值引入的噪声小,但反卷积效果很不好。所以,考虑对K值的取值进行改进,用与系统|X(ω)|的特性相关的函数替代,可以降低噪声的影响,然后对系统频带范围内的估计进行数据建模(AR拟合模型),用插补估计方法处理频带外的数据[13],这时的反卷积效果较为理想,可以提高对噪声的适应能力。通过两种算法的对比图可以看出,用可变函数来代替Snn(ω)/Shh(ω)对维纳滤波器进行改进对噪声有较为明显的抑制作用,进一步提高了反卷积精确度,可以得到较好的辨识效果。
由于维纳滤波器是一种非迭代滤波器,这类滤波器的一个缺点是它不便于引进额外的约束对解进行限制[14]。而增量维纳滤波器允许对解进行迭代估计[15],可以将增量维纳滤波器应用在相关辨识中,这还需要进一步的研究。
[1]罗平安,谬常.反卷积定理-有零点的频谱的反卷积解法[J].核电子学与探测技术,2001(19):454-459.
[2]刘明亮.用卷积运算实现反卷积[J].电子学报,2000,(5): 111-112.
[3]程建政.超声检测图像分辨率的维纳滤波去卷积研究[J].无损检测,2004(26):221-224.
[4]郭建中,陈森林.用维纳逆滤波器解卷积提高超声检测纵向分辨率的改进方法[J].陕西师范大学学报:自然科学版,2004(32):40-42.
[5]李梅,魏文博,等.相关辨识谱激电法[M].北京:地质出版社,2015.
[6]李梅.基于相关辨识技术的时间域谱激电研究[D].北京:中国地质大学,2011.
[7]郑荣.信号处理中的反卷积计算[J].信号处理,1995(11): 82-87.
[8]邓自立,张明波.白噪声Wiener反卷积滤波器[J].控制与决策,2001(16):488-490.
[9]樊昌信.通信原理[M].6版.北京:国防工业出版社,2001.
[10]刘明亮,高剑.迭代频域反卷积滤波器的多参数优化[J].电子学报,2001(12):1661-1664.
[11]郭建中,林书玉.超声检测中维纳逆滤波解卷积方法的改进研究[J].应用声学,2005(24):79-102.
[12]卢涛.基于维纳滤波反卷积的光声成像[J].光学学报,2009(29):1854-1857.
[13]高明哲.噪声对维纳滤波反卷积算法性能影响的分析[J].舰船电子工程,2012(222):35-36.
[14]邹谋炎.反卷积和信号复原[M].北京:国防工业出版社,2001.
[15]王超,高珍,等.基于增量维纳滤波的图像插值算法辨识[J].计算机工程,2010(36):224-226.
The improvement of wiener filtering deconvolution algorithm based on the pseudo-random sequence
ZHEN Xiao-dan,HAO Kai-xue,LI Mei
(School of Information Engineering,University of Geosciences(Beijing),Beijing 100083,China)
The Wiener filtering deconvolution algorithm applied to the correlation identification method which adaptive of noise is unsatisfactory and identification effect is undesirable.The reasons of Wiener filtering deconvolution algorithm in the earth identification process which adaptive of noise is unsatisfactory is analyzed by this undesirable consequence and proposed the improvement algorithm correspondingly:According to test the spectral range of system impulse response processed with a constant obtained bad experimental results.Then,improved algorithm again that using variable function instead of different thresholds,moreover,using different estimation methods to interior of the bandpass and outer of the bandpass to improve the ability to adapt the algorithm noise.Finally,the experiments indicate that the improvement of wiener filtering deconvolution algorithm has better filtering effect to the noise and obtain better recognition effect in the application of the correlation identification method.
correlation identification;wiener filtering deconvolution algorithm;m-sequence;noise
TN91
A
1674-6236(2016)24-0012-03
2016-03-30 稿件编号:201603400
国家自然科学基金(41374185)
甄晓丹(1993—),女,河北涿州人,硕士。研究方向:信号处理。

