基于粒子群混合算法的星载多波束接收天线综合技术研究

胡雪川，刘会杰

（1.中国科学院 上海微系统与信息技术研究所，上海200050；2.上海微小卫星工程中心 上海201210；3.上海科技大学 信息学院，上海200031）

基于粒子群混合算法的星载多波束接收天线综合技术研究

胡雪川1，2，3，刘会杰2

（1.中国科学院 上海微系统与信息技术研究所，上海200050；2.上海微小卫星工程中心 上海201210；3.上海科技大学 信息学院，上海200031）

为了弥补低轨卫星通信系统“远近效应”和“边缘效应”所带来的路径损耗差异，实现对整个扫描区域的"等通量"覆盖。在需求分析的基础上，设计了一个 19阵元7波束的六边形平面阵天线阵，并利用一种基于粒子群（PSO）、萤火虫（FA）混合算法进行优化。该混合算法仿真结果表明，各项指标设计要求能够达到预期，并比传统粒子群算法得到的效果更好。

远近效应；等通量；多波束天线；天线综合；粒子群算法（PSO）；萤火虫算法（FA）

在移动卫星通信系统中，低轨卫星系统相对其他轨道的卫星系统来说，具有传播时延短、路径损耗低、便于用户终端小型化等特点。对于中高轨道卫星，卫星覆盖地球张角小，星下点到覆盖区域边缘的路径损耗差异相对很小，几乎可以忽略。然而，对于低轨卫星而言，卫星覆盖地球张角大，不同张角引起到星地的传播路径不同，传播损耗也不同，“远近效应”和“边缘效应”非常明显[1]，由此造成的差异是不能忽略的，必须采取办法克服。

为了弥补低轨卫星通信系统“远近效应”和“边缘效应”所带来的波束覆盖路径损耗差异，最简单也是最容易实现的办法就是采用多波束叠加覆盖的方案，并对卫星的各个波束进行特殊赋形，实现对整个扫描区域的“等通量”覆盖[2]。所谓“等通量”覆盖，即要求每个波束的增益特性能够补偿从卫星到地面的传播损耗差异。

可见，如何设计多波束叠加覆盖的方案变得非常重要。为了更快更准确的实现波束赋形，在需求分析的基础上，提出一种基于粒子群、萤火虫混合算法优化设计方案。该混合算法仿真结果表明，各项指标设计要求能够达到预期。

1 多波束相控阵天线设计

1.1 理想方向图分析和多波束空间规划

与中高轨卫星不同，低轨道卫星距离地表较近，“远近效应”比较明显。假设卫星高度为900 km，载波频率为1.5 GHz，卫星最大扫描角度为55°，用户从星下点（此时俯仰角θ=0°）到刚刚位于卫星可见范围内（此时俯仰角θ=θmax=55°）的通信链路传输损耗Lf逐渐变大[3]，如图1所示。可以看到，传输损耗最大值和最小值相差6.5 dB，将产生严重的“远近效应”。

为了满足系统设计要求，19个阵元按照三角形栅格排列方式依次排列成一个正六边形[4]，如图2（a）所示。并对19阵元平面阵列天线赋形采用两层规划，如图2（b）所示。第一层为中心波束，主瓣增益不小于10 dB，主瓣宽度为-25°～25°，旁瓣电平不大于-10 dB；第二层即外层分为6个波束，每个波束占据60°，对称排列，主瓣增益不小于12 dB，主瓣宽度为25°～55°，旁瓣电平不大于-10 dB。整个区域的波束覆盖需满足等通量3 dB平坦度[5]。

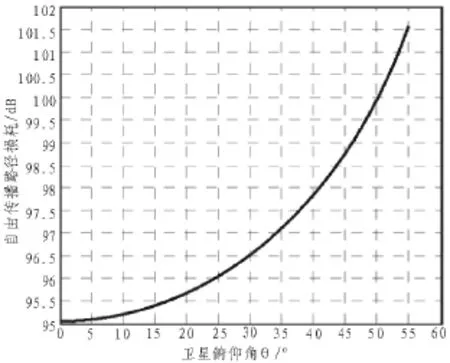
图1 卫星通信链路传输损耗随俯仰角变化情况

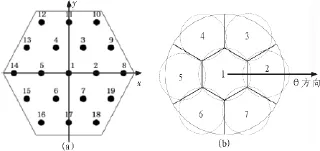
图2 六边形平面相控天线阵及七波束覆盖规划示意图

1.2 天线阵模型分析

根据图2（a）对阵列天线的理想辐射方向图进行建模，以天线辐射中心为坐标原点建立坐标系，则阵因子为：

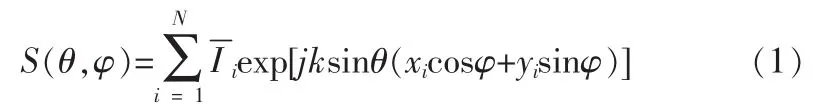
由方向图乘积定理可知，天线方向图为阵因子S（θ，φ）和单元因子fe（θ，φ）的乘积，则该平面阵列天线方向图函数为[5]：

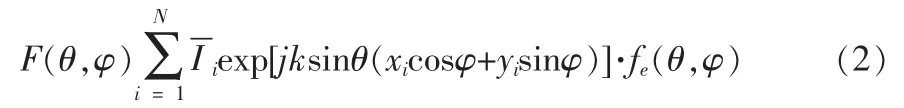
在得到阵列天线方向图函数，整个六边形平面阵天线方向性系数为：

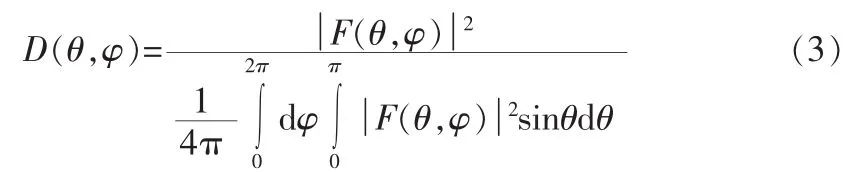
由天线方向性系数可以得到天线增益为：

其中，η为天线的辐射效率，通常在计算过程中将η认为等于1。

2 算法介绍

2.1 粒子群优化算法

粒子群优化算法[6-8]是模拟鸟群的捕食行为，算法的核心是粒子群运动方程：

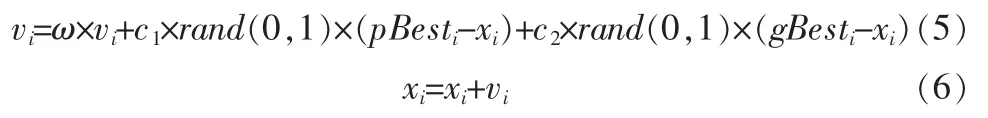
其中，vi是当前个体的速度，xi为当前个体的位置，ω是惯性系数，通常取0.729，c1、c2为学习因子，通常c1、c2都取2，rand（0，1）为在[0，1]之间的随机数，pBesti为当前个体历史最优位置，gBesti为所有个体的全局最优位置。

粒子群优化算法流程简单易实现，算法参数简洁，无需复杂的调整。但缺点是：初始化过程是随机的，这虽然可保证初始解群分布均匀，但个体的质量不能保证。其次，粒子利用自身、个体及全局信息来更新自己的速度和位置，这是一个正反馈过程，当自身信息及个体信息占优势时，算法易陷入局部最优。

2.2 萤火虫算法

萤火虫算法[9-13]是通过模拟萤火虫的群体行为构造出的一类随机优化算法。其算法包含两个要素，即亮度和吸引度。亮度体现了萤火虫所处位置的优劣并决定其移动方向，吸引度决定了萤火虫移动的距离，通过亮度和吸引度的不断更新，从而实现目标优化。

萤火虫的相对荧光亮度I和吸引度β分别为：

其中，I0为萤火虫的最大萤光亮度，即自身（r=0处）荧光亮度，与目标函数值相关，目标函数值越优自身亮度越高；β0为最大吸引度，即光源处（r=0处）的吸引度；γ为光强吸收系数，因为荧光会随着距离的增加和传播媒介的吸收逐渐减弱，所以设置光强吸收系数以体现此特性，可设为常数；rij为萤火虫i与j之间的空间距离。

萤火虫i被吸引向萤火虫j移动的位置更新由公式（9）决定：

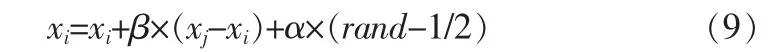
其中，xi、xj为萤火虫i和j所处的空间位置；α为步长因子，是[0，1]上的常数；rand为[0，1]上服从均匀分布的随机因子。

萤火虫算法因为所有个体之间都有充分的信息交流，能执行全局搜索而不易陷入局部极值。缺点是收敛速度较慢。

2.3 粒子群萤火虫混合算法

粒子群优化算法虽然收敛速度快，但容易陷入局部最优。萤火虫算法全局搜索能力强但收敛速度慢。新的混合算法融合了上述两种算法的迭代内涵，使产生的新个体既要兼顾粒子群优化算法的局部寻优特性，又要兼顾萤火虫算法的全局搜索特性。具体实现流程如下[14]:

Step1：参数设置和群体初始化。参数包括:群体规模、最大迭代次数、学习因子、惯性系数、最大吸引力、光在空气中的衰减常数及扰动常数。根据问题维数生成群体规模大小个初始解。

Step2：计算种群的适应度值，满足要求则停止计算，否则进入Step3。

Step3：根据适应度值更新所有粒子的历史最优信息pBest和全局最优信息gBest。如果粒子当前的适应度比其pBest的适应度要好，则用当前粒子位置替换掉pBest位置。如果所有粒子的pBest位置的适应度的最佳值比其gBest的适应度要好，则将取得适应度最佳值的粒子的pBest位置替换掉gBest位置。

Step4：使种群的前一半个体按粒子群算法里的式（5）、式（6）分别作速度、位置更新。该一半个体的全局极值采用整个种群的全局极值；另一半个体按照萤火虫算法里的式（9）作位置移动，对解空间进行充分搜索。并判断全局极值个体是否位于FA群体中，若否，则将其替代FA群体中适应值最差的个体。将两种不同移动规律的群体组合成新的种群，若新个体超出取值范围，则取边界值。

Step5：转入Step2，进入下次迭代，直到满足预设要求，停止迭代。

3 算法性能测试

3.1 Rastrigin函数

该函数的表达式为：

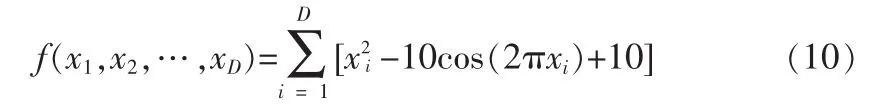
该函数的理论最小值为0，当且仅当x1=x2=…xD=0。这个函数智能算法具有很强的欺骗性，被认为是优化算法很难处理的一个复杂问题[15]。因为它有非常多的局部最小值点和局部最大值点，很容易使算法陷入局部最优，而不能得到全局最优解。优化算法搜索到的解越接近全局最小值，意味着算法全局寻优能力越好。

3.2 性能测试与分析

为了比较粒子群算法、萤火虫算法和新的混合粒子群算法[16]的全局寻优能力，对Rastrigin函数进行性能测试。设置群体规模个数为40，维数D=10，变量取值范围为[-10，10]，最大迭代次数为1 000次。对各种算法的参数设置如下：

1）粒子群算法：惯性系数ω=0.729，学习因子c1=c2=2，粒子飞行速度最大值为0.3。

2）萤火虫算法：最大吸引力β0=1，光在空气中的衰减常数γ=1，扰动因子α=0.2。

3）混合粒子群算法：参数同粒子群算法和萤火虫算法。

图3为3种智能算法对Rastrigin函数寻优的收敛曲线图。从图中可以看出，粒子群算法和混合算法的适应值在250代之后就可以得到一个比较结果。而萤火虫算法需要450代之后才得到一个比较好的结果。但粒子群算法得到最优解不如萤火虫算法和混合算法。粒子群算法收敛速度比较快，而萤火虫算法全局搜索能力更强。混合算法兼顾了粒子群和萤火虫算法的各自优势，既能搜索到更好的解，又以较快的速度收敛。

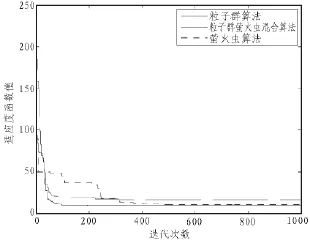
图3 3种算法对Rastrigin函数的迭代收敛曲线图

4 混合粒子群算法在星载多波束天线赋形中的应用

为了将混合算法应用到上述天线综合问题，需要事先确定每个波束的参数的结构和适应度函数。其中，结构如下[5]：

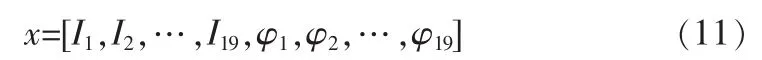
幅度取归一化值，考虑到工程实际情况，限制在0.1～2，相位0～2π。

由于理想方向图主瓣增益G0、主瓣宽度θmain和旁瓣水平SLLexp都已经确定，因此适应度函数直接可以设计为[5]：

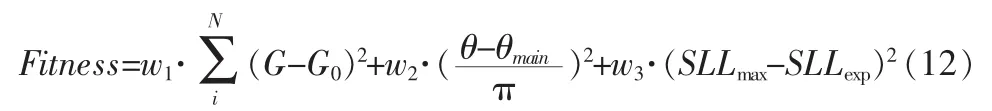
其中，G表示为抽样点的主瓣增益，θ表示主瓣实际半功率宽度，SLLmax表示实际合成波束旁瓣最大增益，w1、w2和w3为权重系数，满足w1+w2+w3=1。

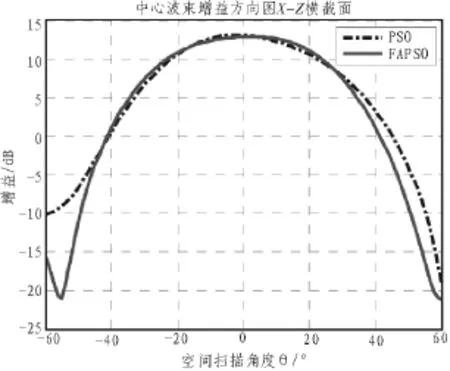
图4 中心波束X-Z平面对比方向图

分别对中心波束和外层第一个波束（波束 2）进行综合优化，将普通粒子群优化算法和混合粒子群算法分别运用到天线综合优化上，算法的参数设置同之前算法性能测试时用到的参数。图4为中心波束分别采用普通粒子群算法和混合粒子群算法得到的X-Z平面对比方向图。图5为波束2分别采用普通粒子群算法和混合粒子群算法得到的X-Z平面对比方向图。可以看到采用混合粒子群算法综合优化后比普通粒子群算法波束增益在边界过渡区下降更快，波束旁瓣水平也明显更低。

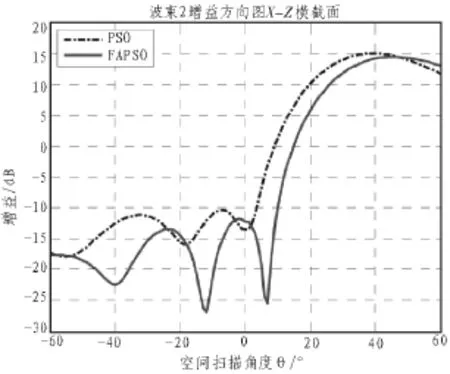
图5 波束2 X-Z平面对比方向图

外层其它5个波束对应的每个阵元幅相值可以根据外层第一个波束按照中心 60°对称关系得到，最终得到图6所示的7个波束的综合方向图。图7为其X-Z平面方向图。

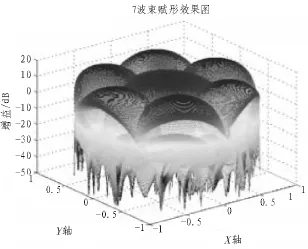
图6 7波束综合方向图

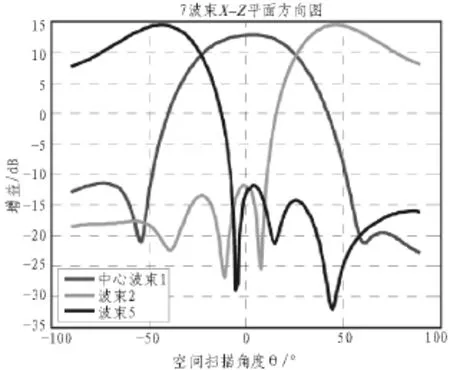
图7 7波束综合方向图X-Z平面方向图

5 结 论

在分析低轨道卫星通信的各项指标后，参考 Globalstar的星载多波束天线，设计了一个19阵元7波束的六边形平面阵天线阵。针对上述天线阵综合优化问题，采用一种粒子群和萤火虫混合优化算法进行优化。该算法以粒子群算法为主，结合萤火虫算法自身的更易搜索全局最优解的优势，弥补粒子群算法的易陷入局部最优解的不足。仿真结果表明，天线设计和算法正确有效，各项指标均符合设计要求。此外，粒子群和萤火虫混合算法比单一粒子群算法收敛速度更快，波束增益在边界过渡区下降更快，旁瓣抑制度性能优化更好。

[1]余金培，杨根庆，梁旭文.现代小卫星技术与应用[M].上海：上海科学普及出版社，2004.

[2]贾铂奇.阵列天线多波束赋形技术研究[D].上海:中国科学院上海微系统与信息技术研究所，2007.

[3]梁广，贾铂奇，龚文斌.星载多波束相控阵天线等通量覆盖设计[J].电波科学学报，2010，25（2）：248-252.

[4]薛正辉，李伟明，任武.阵列天线分析与综合[M].北京:北京航空航天大学出版社，2011.

[5]尚勇，梁广，余金培，等.星载多波束相控阵天线设计与综合优化技术研究宰[J].遥测遥控，2012，33（4）：37-41.

[6]焦永昌，杨科，陈胜兵，等.粒子群优化算法用于阵列天线方向图综合设计[J].电波科学学报，2006，21（1）：16-25.

[7]刘衍民，赵庆祯.粒子群算法的研究及应用 [D].济南：山东师范大学，2011.

[8]李艳丽.基于多目标优化的粒子群算法研究及其应用[D].成都：西南交通大学，2014.

[9]Yang X S，“Firefly algorithms for multimodal optimiza-tion”，Stochastic Algorithms:Foundations and Applications，SAGA [J].Lecture Notes in Computer Sciences 5792，2009：169-178.

[10]Yang X S.Nature-inspired metaheuristic algorithms[M]. Luniver press，2010.

[11]马彦追.萤火虫算法的改进及其应用研究[D].南宁：广西民族大学，2014.

[12]王吉权，王福林.萤火虫算法的改进分析及应用[J].计算机应用，2014，34（9）:2552-2556.

[13]于超杰.萤火虫算法的改进及其在图像阈值分割中的应用[D].兰州：兰州大学，2014.

[14]李章义，万国宾，张静.一种新型混合优化算法及其在星载多波束天线赋形中的应用 [J].现代应用物理，2014，5（4）:322-327.

[15]Mühlenbein H，Schomisch M，Born J.The parallel genetic algorithm as function optimizer[J].Parallel computing，1991，17（6）:619-632.

[16]赵国华，李振华，崔炳喆.基于混合粒子群算法的阵列方向图综合技术[J].电子设计工程，2015,23(23)：158-160.

Research of multi-beam received antenna design and synthesis for LEO satellite based on hybrid particle swarm optimization algorithm

HU Xue-chuan1，2，3，LIU Hui-jie2
（1.Shanghai Institute of Microsystem and Information Technology，CAS，Shanghai 200050，China；2.Shanghai Engineering Center For Microsatellites，Shanghai 201210，China；3.School of Information Science and Technology，ShanghaiTech University，Shanghai 200031，China）

In order to compensate“near-far effect”and“edge effect”caused by the loss difference for LEO satellite communication system and achieve“isoflux”for covering the entire scan area.On the basis of the demand analysis，a hexagonal phased array antenna with 19 elements and 7 beams which is based on Pariticle swarm optimization（PSO）and firefly algorithm（FA）is introduced.Simulation results show that the indicators can achieve the desired design requirements by using the hybrid algorithm，and better than the results by using traditional particle swarm algorithm.

near-far effect；isoflux；multi-beam antenna；antenna synthesis；pariticle swarm optimization（PSO）；firefly algorithm（FA）

TN914

A

1674－6236（2016）24-0001-04

2016-01-18 稿件编号：201601140

国家自然科学基金（61401278）

胡雪川（1993—），男，江西吉安人，硕士研究生。研究方向：卫星通信信号处理。