耦合谐振子网络的自适应包含控制

刘东南，唐 亮，李雪勇，李 玲

（1. 湖南工业大学 理学院，湖南 株洲 412007；2. 湖南铁路科技职业技术学院 电子电气系，湖南 株洲 412006）

耦合谐振子网络的自适应包含控制

刘东南1，唐 亮1，李雪勇1，李 玲2

（1. 湖南工业大学 理学院，湖南 株洲 412007；2. 湖南铁路科技职业技术学院 电子电气系，湖南 株洲 412006）

对具有多个领导者的耦合谐振子网络的自适应包含控制问题进行了研究，提出了基于自适应策略的包含控制协议，运用图论及稳定性理论给出了耦合谐振子网络达到包含的充分条件。最后，通过数值仿真模拟，验证了所提控制方案的有效性。

包含控制；耦合谐振子；自适应控制；多领导者

1 研究背景

由于多智能体系统在生活中的广泛应用[1]，其分布式协调控制得到了许多不同学科的学者们的高度关注[2]。这一研究的一个关键问题是多智能体系统的一致性。所谓一致性是指所有智能体的状态最终收敛到一个期望的值。

根据网络中领导者的个数，一致性又可分为无领导者一致性，领导者-跟随一致性（一致性跟踪），集合跟踪一致性（包含）。近年来，由于包含控制具有广泛的应用背景，多智能体系统的包含控制成为多智能体系统的一个热点问题[3-5]。文献[3]利用滑模控制理论，研究了具有有界干扰的非线性多智能体系统的有限时间一致性与包含控制。文献[4]讨论了无速度测量的二阶积分器型多智能体系统的包含控制问题，分别利用速度估计器和采样控制的方法，设计了不依赖于速度测量的包含控制协议，并分别给出了包含达到的充要条件。文献[5]运用Lyapunov稳定性理论、代数图论和矩阵理论，研究具有有界外部干扰的耦合谐振子网络的一致性问题。

耦合谐振子网络是一类重要的物理系统，许多实际系统都可由耦合谐振子网络描述，关于耦合谐振子网络的同步（一致性）问题受到越来越多的学者关注。文献[6]利用矩阵论的相关知识，研究了无向固定拓扑下耦合谐振子网络的同步问题。文献[7]考虑了无向动态拓扑下耦合谐振子网络的同步问题，并利用Lyapunov稳定性理论给出了收敛性分析。以上文献主要针对网络中存在单个领导者的情形展开研究，实际中，确实存在多领导者情形的耦合谐振子网络。基于此，文献[8]设计了自适应的连边权重，研究了耦合谐振子网络的聚类一致性问题。但关于耦合谐振子网络的包含控制的文献却并不多见。笔者通过大量检索发现，仅有文献[9]研究了有向拓扑下耦合谐振子网络的包含控制问题，并给出了包含达到的充要条件。但文献[6-7, 9]中，同步或包含达到的条件依赖于网络的拓扑结构，从而不是完全分布式的。因此，本文主要研究在网络中存在多个领导者的情形下，耦合谐振子网络的自适应包含控制问题，并引入自适应控制策略，使得包含达到的条件不依赖于网络Laplacian矩阵中跟随者所对应子块的特征值，从而保证包含协议是完全分布式的。

2 模型介绍和预备知识

在耦合谐振子网络中的第i个节点的动态可以表示为

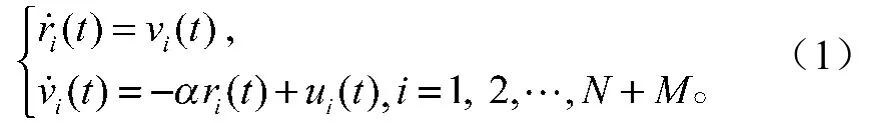
N, M是正整数，分别表示网络中跟随者和领导者的数目，且第1, 2, …, N个节点为网络中的跟随者，第N+1,…, N+M个节点为网络中的领导者，其中跟随者集合用F表示，领导者集合用L表示。

网络的拓扑可以用图定义，其中有向图G=(V, E)由非空的顶点集和边集组成。图G的邻接矩阵A= (aij)定义为：aij=1当且仅当。关于图的相关知识可参见文献[10-11]。网络的Laplacian矩阵L=(lij)被定义为：。

定义1 如果网络中的一个节点的邻域为空集，则称这个节点对应的智能体为领导者；否则，称为跟随者。

根据网络中跟随者与领导者及Laplacian矩阵的定义可知，L可以写成分块矩阵形式

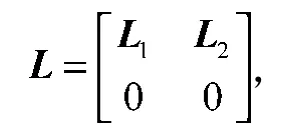
式中：L1表示跟随者所对应的Laplacian子块；

L2表示跟随者与领导者之间邻接关系所对应的Laplacian子块。

本文主要研究具有多个领导者的耦合谐振子网络的包含控制问题，即设计有效的控制算法，使得网络中的跟随者渐近进入领导者所形成的凸包络中。

假设1 假定网络中跟随者之间的通信是无向的，即网络的Laplacian矩阵多对应的跟随者子块是对称的。

假设2 假定对每一个跟随者，至少存在一个领导者有一条有向的路径通往这个跟随者。

引理1[4]若假设1和假设2成立，则L1正定，且-L1-1L2的每个元素都非负，-L1-1L2的每一行的行和为1。

3 主要结果

对网络中第i个智能体，可提出如下控制算法：

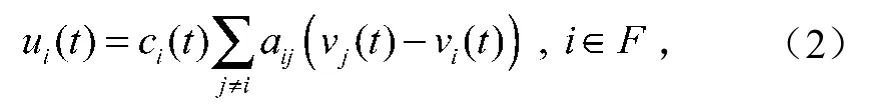
式中ci为包含协议的自适应增益，且满足

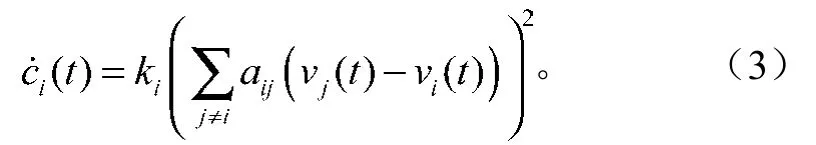
由aij的定义可知，当i L时，aij=0，从而ui(t)=0。令

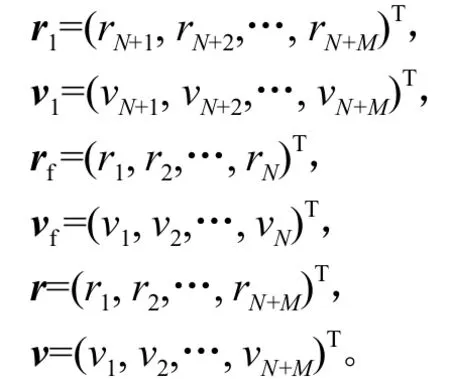
由于领导者的控制器为0，不难得到领导者的轨迹方程为

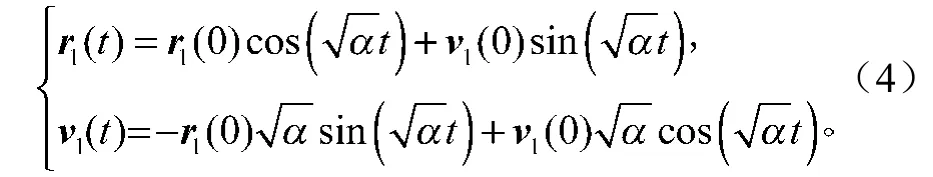
式中rl(0), vl(0)分别表示领导者作成的向量的位置和速度的初始值。

将控制协议式（2）及自适应策略式（3）代入系统式（1），可得

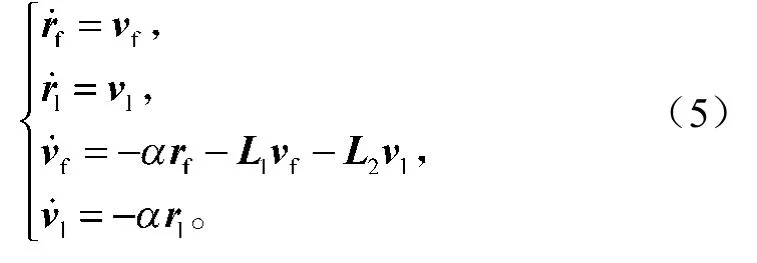
定理1 若假设1和假设2成立，则耦合谐振子网络式（1）在包含控制协议式（2）及自适应策略式（3）的作用下达到包含，且网络中的跟随者满足

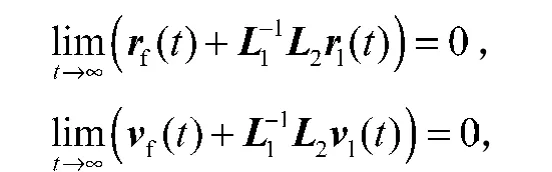
式中rl(t)与vl(t)由式（4）给出。

证 由引理1可知，若假设1和假设2成立，则L1正定，从而可逆。令误差变量

由定理1可知，在包含控制协议式（2）及自适应策略式（3）下，耦合谐振子网络式（1）能否达到包含，并不依赖于网络Laplacian矩阵中跟随者所对应的子块的特征根，而仅需网络的初始拓扑为连通的，这就保证了本文中所提出的协议是完全分布式的。

4 数值仿真

考虑具有3个领导者和6个跟随者的耦合谐振子网络，其拓扑图如图1所示。易知，假设1和假设2成立。

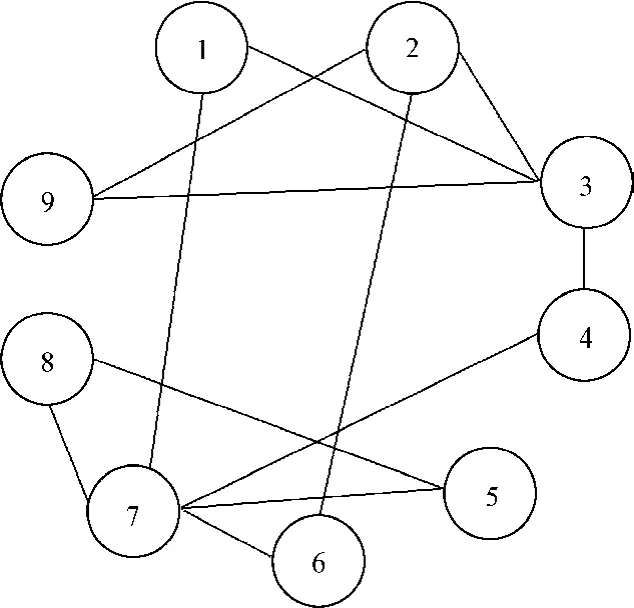
图1 耦合谐振子网络的拓扑图Fig. 1 Coupled harmonic oscillators network topology

网络的第i个节点具有如下动态：

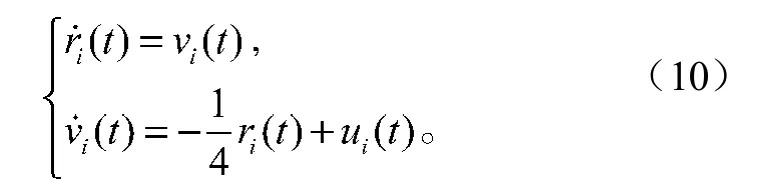
耦合谐振子的位置轨迹及速度轨迹分别如图2和图3所示。由图可知，网络中的跟随者位置，最终进入到领导者所形成的三角形（图三边形）中。

图2 耦合谐振子的位置轨迹Fig. 2 Position trajectory of coupled harmonic oscillators

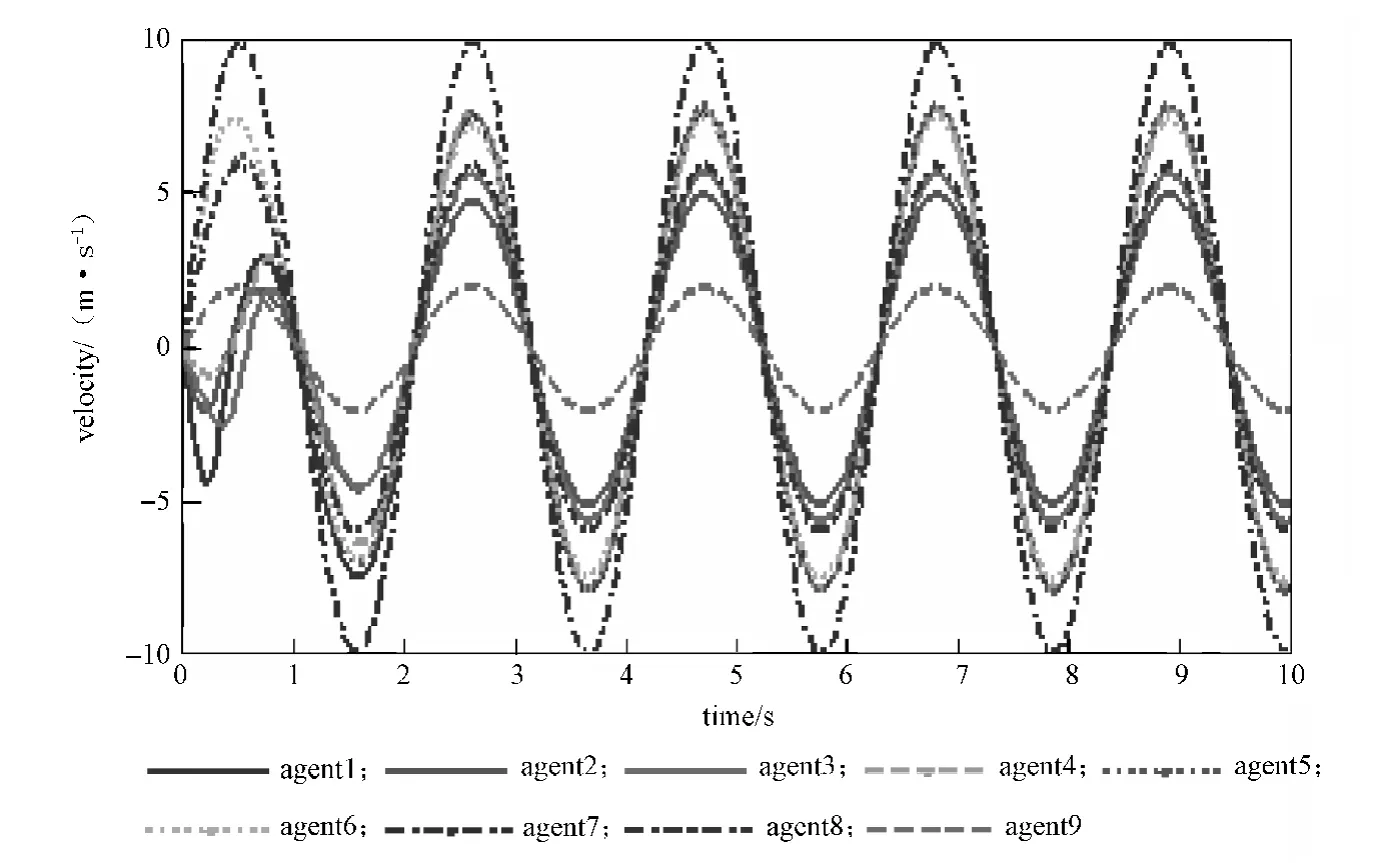
图3 耦合谐振子的速度轨迹Fig. 3 Speed trajectory of coupled harmonic oscillators

5 结语

本文对具有多个领导者的耦合谐振子的分布式自适应包含控制问题进行了研究。在固定的网络拓扑下，利用自适应控制策略设计有效的包含控制协议，使得网络达到包含的条件不依赖于网络Laplacian矩阵跟随者所对应的子块的特征根，从而保证了所提出的包含算法是完全分布式，并利用数值仿真例子验证了所提出的控制方案的有效性。

[1]STROGATZ S H. Exploring Complex Networks[J]. Nature，2001， 410：268-276.

[2]汪小帆，李 翔，陈关荣. 复杂网络理论及其应用[M].北京：清华大学出版社，2006：16. WANG Xiaofan，LI Xiang，CHEN Guanrong. Complex Networks Theory and Its Application[M]. Beijing：Tsinghua University Press，2006：16.

[3]ZHANG Y J，YANG Y，ZHAO Y，et al. Distributed Finite-Time Tracking Control for Nonlinear Multi-AgentSystems Subject to External Disturbances[J]. International Journal of Control，2013，86(1)：29-40.

[4]XU C J，ZHENG Y，SU H S，et al. Necessary and Sufficient Conditions for Distributed Containment Control of Multi-Agent Systems Without Velocity Measurement [J]. IET Control Theory Applicat，2014 ，8(16)：1752-1759.

[5]范龙云，朱善华，徐承杰，等. 具有有界干扰的耦合谐振子网络的一致性[J]. 湖南工业大学学报，2015，29(5)：102-106. FAN Longyun，ZHU Shanhua，XU Chengjie，et al. The Consistency of Coupled Harmonic Oscillator Network with Bounded Disturbance[J]. Journal of Hunan University of Technology，2015，29(5)：102-106.

[6]REN W. Synchronization of Coupled Harmonic Oscillators with Local Interaction[J]. Automatica，2008，44(12)：3195-3200.

[7]SU H S，WANG X F，LIN Z L. Synchronization of Coupled Harmonic Oscillators in a Dynamic Proximity Network[J]. Automatica，2009，45(10)：2286-2291 .

[8]SU H S，CHEN M Z， WANG X F， et al. Adaptive Cluster Synchronisation of Coupled Harmonic Oscillators with Multiple Leaders[J]. IET Control Theory and Applications，2013，7(5)：765-772.

[9]XU C J， ZHENG Y，SU H S，et al. Containment Control for Coupled Harmonic Oscillators with Multiple Leaders Under Directed Topology[J]. International Journal of Control，2015，88(2)： 248-255.

[10]GODSIL C，ROYLE G. Algebraic Graph Theory[M]. New York：Springer，2001：76-90.

[11]徐承杰，易 忠，郑 英. 形式三角矩阵环的零因子图[J]. 数学杂志，2013，33(5)：891-901. XU Chengjie，YI Zhong，ZHENG Ying. On the Zero-Divisor Graphs of Formal Triangular Matrix Rings[J]. Journal of Mathematics，2013，33(5)：891-901.

（责任编辑：邓光辉）

《湖南工业大学学报》被评为“2016年度中国高校优秀科技期刊”

据中国高校科技期刊研究会网站（http://www.cujs.com/index.asp）发布的“杰出·百佳·优秀科技期刊入选名单公示”，《湖南工业大学学报》被评为“2016年度中国高校优秀科技期刊”。

此次评选在利用全文数据库、检索数据库和评价机构等的有关评价成果的同时，采用分类、分层次遴选方法，对参评期刊所获荣誉、传播与利用效应、学术影响力与行业影响力、政治与编辑出版质量等进行全面评价，择优遴选。

Distributed Adaptive Containment of Coupled Harmonic Oscillators Networks

LIU Dongnan1，TANG Liang1，LI Xueyong1，LI Ling2
（1. School of Science，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. Department of Electronic and Electrical Engineering，Hunan Vocational College of Railway Technology，Zhuzhou Hunan 412006，China）

A research has been conducted on the distributed adaptive containment of the networks of coupled harmonic oscillators under fixed topologies, a containment protocol based on adaptive strategies has been proposed, and a sufficient condition for distributed containment of coupled harmonic oscillators has thus been obtained, based on stability and matrix theory. As a result, a numerical simulation verifies the validity of the proposed containment protocol.

containment；coupled harmonic oscillators；adaptive control；multiple leaders

TP13

A

1673-9833(2016)05-0032-05

10.3969/j.issn.1673-9833.2016.05.007

2016-05-29

湖南工业大学自然科学研究基金资助项目（2014HZX23），湖南省教育厅科研基金资助项目（15C0405，13C020，12C0088），湖南省自然科学基金资助项目（2015JJ2045）

刘东南（1983-），男，湖南邵阳人，湖南工业大学讲师，硕士，主要研究方向为混合系统的稳定性与控制，E-mail：ladn55555@163.com

唐 亮（1978-），男，湖南祁阳人，湖南工业大学讲师，硕士，主要研究方向为双调和分析，E-mail：123643897@qq.com