数字卷积加减速控制算法研究

邱焕能，欧元贤

（华南理工大学 机械与汽车工程学院，广州 510640）

数字卷积加减速控制算法研究

邱焕能，欧元贤

（华南理工大学 机械与汽车工程学院，广州 510640）

数控系统的加减速控制是其关键技术之一。提出了一种新颖的基于数字卷积的加减速控制算法，可使数控系统在加工过程中实现平滑连续的运动，保持加速度连续变化，避免急速的运动带来的机构磨损、系统冲击、共振等问题，保证加工精度。推导了连续数字卷积规划方法的数学表达式，并给出了算法的具体实现步骤，实验结果证明了算法的有效性及实用性。相比于传统的S曲线加减速规划，该算法的计算效率大为提高。

数字卷积；加减速控制；数控系统；S曲线

0　引言

现代加工领域对高精度高速度加工的要求越来越高，而速度控制是其中的核心技术。在数控加工中，为保证加工的精度，应避免急速的运动带来的系统冲击、共振等问题，机床的运动应具有平滑性。现阶段常用的加减速控制方法有直线加减速、S曲线加减速等方法。直线加减速[1]的优点是计算简单，对硬件要求不高，但其缺点也是十分明显：在加减速阶段其加速度有突变，对数控系统产生冲击，影响加工精度。S曲线加减速在高性能数控系统中更为常用，在文献[2]中，其将加减速过程分段考虑，通过对加加速度的控制来限制速度的变化。但是这种方法将加减速过程分为加加速段、匀加速段、减加速段、匀速段等七个阶段，再分别计算每个阶段的速度，以实现加速度连续的加工过程，其计算繁复，实现复杂。近年来，还有其他的柔性加减速算法被提出来。文献[3]提出运用滤波技术，在传统的直线加减速算法后串联一个滑动平均滤波器，对速度进行平滑规划，并证明了对直线加减速算法做滑动平均规划与S曲线加减速等效。Jeon Jae Wook[4]提出，基于多项式的加减速方法为满足约束条件，其计算量将随多项式阶数以指数方式增加，计算负担非常大。他提出了一种基于卷积的加减速方法，能够高效的得到平滑过渡的曲线。在此基础上，Geon Lee[5]提出了一种新颖的基于卷积的轨迹生成方法，通过引入约束条件，可得到高阶连续的运动轨迹。

论文以数字卷积理论为基础，提出了数控系统中基于数字卷积的加减速控制算法，详细推导了数字卷积加减速控制算法的数学表达式，并给出了算法的具体实现步骤。

1　卷积运算

卷积是一种数学运算，对两个函数进行卷积运算可得到一个新的函数，其定义如下：

假设h(t)与x(t)为参与卷积的两个函数，输出为y(t)。定义h(t)是一个面积为1的矩形函数：

函数x(t)为定义于0≤t≤tx的任意函数，满足狄利克雷（Dirichlet）条件[6]，由此可得到：

上述的卷积运算有以下三个性质：

1）时间延长：y(t)的非零域相比x(t)延长th时间。

2）积分不变：y(t)与x(t)二者的积分相同，即：

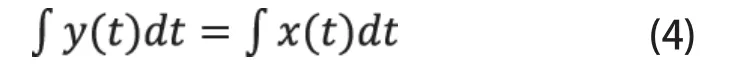
证明过程如下：

假设X(s)，H(s)，Y(s)分别为x(t)，h(t)与y(t)的拉普拉斯变换，那么，的拉普拉斯变换可表示为X(s)/s，同样，的拉普拉斯变换可表示为Y(s)/ s。由卷积定理可得：

由终值定理：

其中，H(s)可表示为：

运用洛必达法则：

因此：

3）最大值有界：经过卷积运算后的y(t)的最大值不大于x(t)的最大值。

假设x(t)与y(t)的最大值分别为xm，ym，y(t)在tm时刻有最大值，故：

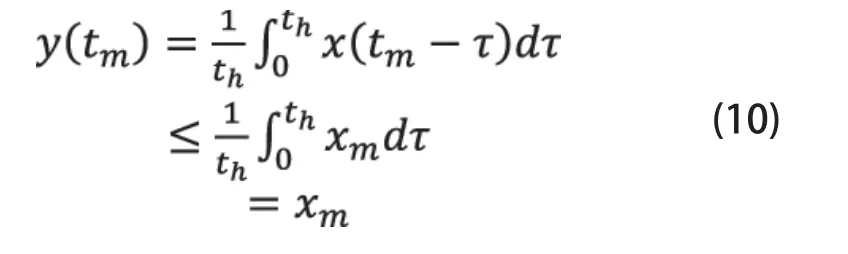
特别的，当x(t)在不小于th的时间历程里都维持x(t)=xm时，ym=xm。

2　连续卷积

若机床沿直线从点P0运动至点P1，两端点距离为L。假设加工过程中数控系统的最大进给速度为vm，加速度为速度的一阶导数，即a=dv，am表示最大加速度；同理，加加速度表示为，最大加加速度为。令：

公式(11)中，v0=vm，t0=L/vm。y0(t)与坐标轴包围的矩形面积即为L。

将y0(t)与h(t)作卷积运算，输出为y1(t)，再对y1(t)作一次卷积运算得到y2(t)。通过连续的两次卷积运算，可以从一个矩形的速度方波得到S型的加减速速度曲线，如图1所示。

图1　对矩形函数连续卷积

假设0≤th≤t0，可求出y1(t)的表达式为：

再对y1(t)作一次卷积运算，得到：

可知加速度a为分段连续的一次函数：

若加速度最大值表示为am，其加加速度最大值表示为，则：

dy2(t)及ddy2(t)的曲线图如图2、图3所示。

图2　卷积函数的一阶导数

图3　卷积函数的二阶导数

因此，若数控系统以y2为进给速度曲线，其在整个加工过程中将经历平滑的加减速过程，系统的加速度连续变化。由加加速度的变化可将这个过程分解为加加速阶段、减加速阶段、匀速段、加减速阶段、减减速阶段，加加速度的值在各个阶段中均是定值。

由第1节卷积运算的三个性质还可知道，将系统的进给速度进行卷积规划后，

1）时间延长：加工时间将延长2th；

2）终点可达：经过速度规划后执行部件仍可达到预定目标点；

3）速度限制：卷积后的速度不超过原来的最大速度。

3　数字卷积

在数控系统中，执行部件的运动需要用插补算法控制，在已知点间的路径上插补一系列的期望中间点，因此需要将连续卷积法转化为离散领域中的卷积运算，称为数字卷积。假设从A点运动到B点的时间历程为t，插补周期为Ts，th为h(t)的脉冲宽度。假设0≤th≤t，定义：

由式(19)和式(20)可知，应用数字卷积法求解插补点的速度值可通过递归方法求得，只包含加法和除法运算。相比传统的S曲线加减速控制算法，其表达高效简洁，计算量大为减少。

4　数字卷积算法的实现

以直线运动为例，连续数字卷积加减速控制算法的规划过程如下：

1）给定初始条件

（1）给定初始点位置P0、最终点位置P1；

（2）给定约束条件：最大进给速度vm、最大加速度am、插补周期Ts。

2）求解运动的长度L

从点P0运动至点P1，那么P0P1可表示为：

P0与P1的距离L为：

其单位方向的矢量为：

3）由约束条件求解插补点个数n、m

4）运用数字卷积法求解插补点的速度vi

令y0=vm，由式(19)和式(20)分别求出各个插补点的速度vi。其中，0≤i≤n+2m。

5）求解插补点的位置坐标

插补点到初始点的距离si为：

则Pi的坐标也可表示为：

5　计算实例

在MATLAB软件上实现上述的直线运动规划，令初始点与目标点的坐标分别为：

单位为mm。限制最大进给速度为200mm/s，加速度最大值为1000mm/s2，插补周期设为1ms。经过插补之后得到的系统运动如图4所示，求解其速度及加速度，列为图5。

图4　直线加减速运动（mm）

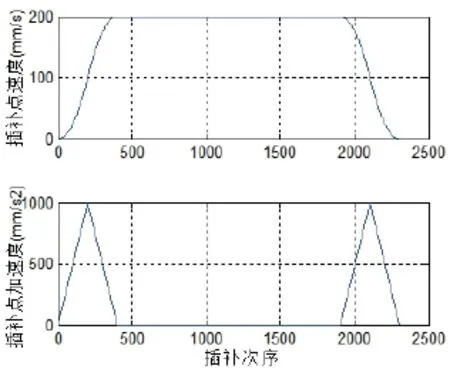
图5　插补点速度（mm/s）及加速度（不考虑方向）（mm/s2）

由图5可以看到，系统在作直线运动时，加速度在前后的加减速阶段其波形呈三角形，其最大值在限制条件内，在中间阶段恒为零；加速度连续变化，没有产生突变。所得到的速度曲线变化平滑，没有冲击，在经过了平滑加速后速度达到稳定，并维持在额定的最高速，最后再经过平滑减速后降为零。

6　结论

在现代加工过程中，数控系统的运动应具有平滑性，加减速过程中应避免加速度的突变，避免其带来的系统冲击、共振及机构磨损等问题，以保证加工精度。现阶段常用的加减速控制方法有直线加减速、S曲线加减速等方法。直线加减速计算简单，但加工过程中加速度有突变；S曲线加减速具有良好的柔性，但其计算繁复，实现复杂。论文提出了一种基于数字卷积的柔性加减速控制算法，可使系统在加工过程中保持加速度连续变化。首先详细推导了数字卷积法的数学表达式，并证明了经过数字卷积规划后系统具有良好的柔性，然后给出了算法的具体实现步骤，最后通过实例证实了算法的有效性。

[1] 胡建华,廖文和,周儒荣.CNC系统中几种升降速控制曲线的研究与比较[J].南京航空航天大学学报,1999,06：706-711.

[2] 郭新贵,李从心.S曲线加减速算法研究[J].机床与液压, 2002(05)：60-62.

[3] 于东,胡韶华,盖荣丽,等.基于滤波技术的数控系统加减速研究[J].中国机械工程,2008(07)：804-807.

[4] Jeon Jae Wook, Ha Young Youl.A generalized approach for the acceleration and deceleration of industrial robots and CNC machine tools[J].IEEE Transactions on Industrial Electronics, 2000,47(1)：133-139.

[5] Geon Lee, Kim J, Choi Y. Convolution-based trajectory generation methods using physical system limits[J].Journal of Dynamic Systems, Measurement, and Control,2013,135(1)：11001.

[6] 刁元胜.积分变换[M].广东：华南理工大学出版社,2003：76-79.

Study of digital convolution based acc/dec control algorithm

QIU Huan-neng, OU Yuan-xian

TP271+.4

A

1009-0134(2016)07-0065-04

2016-03-16

广州市科技计划项目资助（2013J4300012）

邱焕能（1991 -），男，广东汕尾人，硕士研究生，研究方向为机器人控制和先进加工技术。