水中人工心脏泵用磁轴承系统的模型及控制研究

孙 坤，陈 琛

（苏州大学 机电工程学院，苏州 215021）

水中人工心脏泵用磁轴承系统的模型及控制研究

孙 坤，陈 琛

（苏州大学 机电工程学院，苏州 215021）

提出水环境下磁悬浮血泵转子运动模型，将水对泵转子的作用等效成弹簧阻尼器，利用ADAMS与Simulink联合仿真；并针对水中磁悬浮血泵，通过分析并调整PD控制器的微分系数，实现在保证转子稳定性能的同时，改善转子位移信号。

人工心脏泵；阻尼器；PD调节；改善信号

0　引言

磁轴承由于具有无机械摩擦、无接触磨损、无需润滑、定位精度高、转速高且对环境无污染[1]等优点逐渐被人工心脏[2]、电主轴机床[1]等领域所应用。作为典型的开环非稳定系统，电磁轴承通过主动控制器，利用可控电磁力为悬浮转子提供高精度的定位控制和振动阻尼控制[3]。

人工心脏用电磁轴承是在血液中工作的，但目前其建模以及控制器设计与一般工业用电磁轴承类似[4]，都是在空载环境下所进行的，再经过增益等方面的调节，使得血泵在液体中运行稳定。建模上的误差无疑会导致磁悬浮系统运行性能较差，也阻碍了人工心脏用磁轴承的研制进程。另外对于磁悬浮血泵这类不规则的几何模型，在水、血液等流体中的运动模型目前也很少有理论上研究。针对苏州同心医疗公司的新一代磁悬浮人工心脏泵，如图1所示，本文提出了水中磁悬浮系统模型，通过在ADAMS中建立机械模型，与Simulink联合仿真。针对所使用的经典PD控制，考虑到水中磁轴承系统本身存在阻尼，对微分环节作适当减弱，以改善信号输出。

图1　同心医疗China Heart III磁悬浮人工心脏

1　磁悬浮系统理论建模

磁悬浮血泵同一般主动磁轴承原理相同，由径向两自由度（或四自由度）和轴向一自由度构成，因转速不是太高且为刚性转子，完全可以忽略陀螺效应，故其可以解耦为单自由度磁悬浮系统分别进行控制，这样也方便了简单PD控制器的应用。

对于水中磁悬浮系统，本文根据[1]关于单自由度磁悬浮系统模型，以及将水冲击力视为平衡点附近位移和速度的函数[5]，写出当泵转子在静平衡位置附近作小振动时，运动方程可以写为：

其中，m为泵转子质量，x为转子径向位移，kx为位移-力刚度系数，ki为电流-力刚度系数，kxx、kxv、kxv、cxx和cxy分别为转子受水影响的刚度和阻尼系数。

从式(1)可以看到，一般磁悬浮只有负刚度，缺少阻尼项，所以是典型的开环非稳定系统，而PD控制的比例与微分环节实质上就是调整磁悬浮系统的刚度，并增加其阻尼成分[6]。而对于水中的磁悬浮泵，水对泵转子恰好可以增加其阻尼项。

该型人工心脏用磁悬浮转子为圆环状，其顶端焊有叶片，水、血液等流体对该类型物体的作用较为复杂，很难从理论上进行推导研究，故本文将流体对泵转子的作用等效为弹簧阻尼力。根据[7]及本磁悬浮系统结构参数，如表1所示，可以大致计算出c=30Ns/m，k=0.5N/m（忽略y方向对x方向耦合）。本文再对该泵环路测试，得到环路传输特性图（如图2所示）。从图中可以看出，水载测试中，其阻尼增加值与计算值偏差不大，说明水中泵转子运动模型较为合理。初取c=24Ns/m，k=0.5N/m，以便在ADAMS与Simulink仿真中作微调。

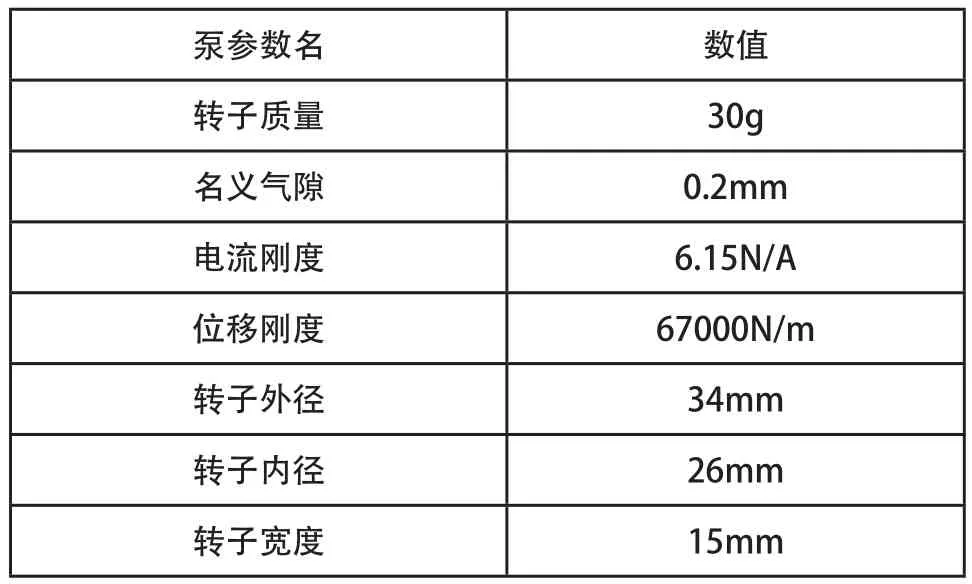
表1　系统结构系数

图2　人工心脏泵环路传输特性

2　ADAMS与Simulink联合仿真

磁轴承系统研究一般把其力学系统看作传递函数，通过MATLAB/Simulink对磁悬浮轴承整体系统进行仿真的，但是这种仿真在建立系统机械模型时，尤其是在液体环境下，不够精确，而ADAMS能够更好地综合考虑各个因素对磁悬浮轴承整个系统的影响，对现实的实验也具有更好的指导意义[8]。

首先在SolidWorks建立磁悬浮泵的几何模型，把它导入ADAMS里面。在ADAMS中定义定子固定约束，转子为平面副，并设置与定子碰撞接触。为了考虑水对泵转子的作用，在泵转子与定子之间建立径向均布5个弹簧拉压阻尼器，其阻尼即为上文所计算值。设置状态变量有x、y方向径向力x、y方向位移，并将x、y方向径向力设为输入变量，x、y方向位移设为输出变量。

控制系统是用MATLAB/Simulink模块来设计，由上述可知，磁悬浮泵式不稳定的，因此采用PD控制对系统仿真，环路还包含一个相位超前环节以及传感器低通、功率放大器环节，如图3所示。图4(a)是未考虑阻尼时的阶跃响应，图4(b)是考虑了阻尼的响应，可以发现考虑阻尼时的响应时间稍慢些，但超调量很小。说明水抑制了泵转子的振荡，改善了泵转子的性能。并通过对该泵进行空载与水载起浮试验（如图5所示，a.空载，b.水载），可以看出水载时的起浮较为平稳，大约需要5ms，而空载时稍快一些。通过微调ADAMS模型中的阻尼值至c=20Ns/m，响应时间相当吻合。

图3　磁悬浮系统ADAMS/Simulink联合仿真模块图

图4　磁悬浮系统阶跃响应模块

图5　磁悬浮泵空载与水载起浮试验

3　PID微分环节的调节

从图6(a)可以看出，空载时的转子起浮是稳定的，满足性能要求，只是在起浮后期有170ms的振荡，而水载时图6(b)几乎没有振荡。因此，我们可以针对该人工心脏泵，考虑放宽微分环节，以此减弱微分对高频噪声放大的影响。本文共设置了递减的4个微分系数Td=0.0013288、0.0011、0.00077和0.00044（通过改变电阻值），分别探究泵转子起浮性能及位移信号的改善程度。

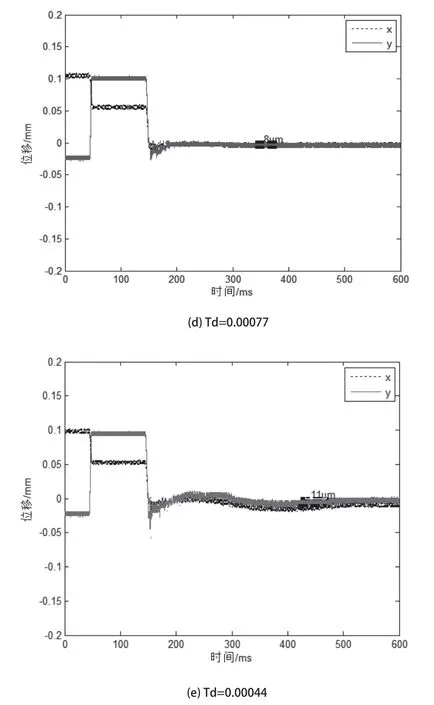
图6　各不同条件下泵转子全起浮过程位移输出（a.空载, b-e.水载）

从图中可以看出，在Td降至0.0011时，起浮很好，并未出现振荡，位移信号有所改善。当降至0.00077时，起浮仍然稳定，稍有振荡，但位移信号含噪量明显降低。再降至0.00044时，有明显振荡，振幅达到50um，位移信号未出现改善，此时表明系统已出现阻尼不足，趋向不稳定，更起不到对输出信号的改善作用。因此表明，针对水中磁悬浮运行的控制系统可以空载控制系统为基础，且充分利用水中模型的特点，适当调节微分环节，达到实现稳定性能良好的同时改善输出信号质量。

4　结论

本文针对人工心脏泵用磁悬浮系统，建立了水中磁悬浮系统模型，引入阻尼项，并借助ADAMS与Simulink联合仿真，表明了水对磁悬浮泵转子振荡的抑制作用。又通过调节空载下PD控制器的微分项，减弱对微分的需要，探索水的作用对于磁悬浮系统阻尼的放宽程度，从而在保证泵转子性能稳定且良好的同时降低位移噪声。

【】【】

[1] Gerhard Schweitzer, Eric H. Maslen.Magnetic Bearings-Theory, Design,and Application to Rotating Machinery[M]. New York： Springer,2009.

[2] Nojir, C.,Kiijima,T.,Maekawa,J..Recent Progress in the Development of Termo Implantable Left Ventricular Assist System[J].ASAIO Journal,1999,45(3)：199-203.

[3] 谢振宇,张景亭,高华,等.带阻尼器磁悬浮轴承转子系统的不平衡响应[J].中国机械工程,2009,20(3)：327-330.

[4] 雷世东,袁小阳.人工心脏电磁轴承概念设计的知识基础[J].机械科学与技术,2004,23(3)：293-296.

[5] 闻邦椿,顾家柳,夏松波,等.高等转子动力学[M].北京：机械工业出版社,2000.

[6] A. Chiba,T.Fukao,O.Ichikawa. Magnetic Bearings and Bearingless Drives[M].Oxford：Elsevier,2005.

[7] 董跃.液压轴承油膜稳定性分析[J].机电产品开发与创新,2012,25(5)：155-157.

[8] 冯恒.磁悬浮轴承系统仿真研究[D].南京航空航天大学,2010.

Research on model and control of magnetic bearing applied in artifi cial heart in the water

SUN Kun, CHEN Chen

TH133.3

A

1009-0134(2016)07-0005-04

2016-03-19

孙坤（1992 -），男，江苏涟水人，硕士研究生，研究方向为人工心脏、磁悬浮轴承控制以及有限元仿真等。