基于多算法的永磁同步电机伺服控制系统

李志宏，吴连顺，李玉萍，钱晨亮，刘 杰

（1.武汉理工大学 自动化学院，武汉 430070；2.武汉船用机械有限公司，武汉 430084）

基于多算法的永磁同步电机伺服控制系统

李志宏1，吴连顺1，李玉萍1，钱晨亮1，刘 杰2

（1.武汉理工大学 自动化学院，武汉 430070；2.武汉船用机械有限公司，武汉 430084）

为了提高伺服控制系统的动态性、鲁棒性以及良好的跟踪性能，以永磁同步电机数学模型为基础提出了滑模变控制与卡尔曼观测器相结合的控制方案。在伺服控制系统中，位置环采用滑模变结构控制，速度环主回路采用PID控制，其反馈回路中使用卡尔曼观测器的控制策略，而电流环采用PI控制。在MATLAB/Simulink环境中，对多种控制算法相结合的控制系统进行仿真，证明了此方案的有效性，即电机在各种扰动及不确定因素情况下仍具有较强的适应性和鲁棒性，发挥了良好的的动态特性。

永磁同步电动机；滑模变结构；卡尔曼观测器；MATLAB/Simulink

0　引言

永磁同步电机以结构简单、效率高、力矩大以及高控制精度等优良品质被广泛应用于伺服控制领域。高品质的伺服控制系统需要在各种外界干扰的情况下达到稳定转速、精确的位置跟踪，而单纯的PID控制已经不能满足这一需求。文献[1]提出了基于自抗扰控制的伺服系统，该策略不依赖被控对象模型，而是通过补偿扰动来获得良好的性能，同时它也适用于非线性系统。文献[2]提出了基于模糊RBF神经网络的伺服系统，该方法通过在线学习进行调整参数，使系统保持良好的控制效果，但是控制算法复杂。文献[3]提出了基于抗差扩展卡尔曼滤波器的电机转速估计，该方法减小了粗差对估计值状态的影响，能准确地估计转速。文献[4]提出了基于卡尔曼滤波器的电机转速精确控制，该方法算法简单，计算量小，效果很好，适用于低速环境。文献[5]提出了基于指数趋近律的滑模变控制结构，该方法能够减小外界干扰以及参数变化对系统的影响，指数趋近律削弱了滑模切换造成的高频抖振。在前人的研究基础上，本文提出了基于多算法相结合的控制策略，卡尔曼滤波器精确估计电机转速，滑模变结构按系统需求设计实现位置环的快速平滑跟踪。仿真表明了该伺服系统满足较高的性能要求。

1　永磁同步电机数学模型

由于永磁同步电机是一个复杂的系统，为了方便地对它进行分析和求解，在允许误差的范围内，通常利用3s/2r变换将三相静止坐标系变换到两相旋转坐标系中。本文采用id=0的矢量控制方式，可以得到在d、q坐标系上永磁同步电机的解耦状态方程[6]：

式中，R为电机绕组等效电阻；Lq为等效q轴电感；np为极对数；w为转子角速度；Ψr为转子等效磁链；TL为负载转矩；iq为q轴电流；J为转动惯量。

此系统采用典型的三环控制，在各个控制环上施以不同的控制策略，从而使控制系统的性能得到优化。永磁同步电机矢量控制总体框图如图1所示，主要包括：位置滑模变模块、转速PID调节模块、电流PI调节模块、卡尔曼滤波模块、SVPWM发生器模块、电压逆变器模块以及电机本体模块。

2　控制器设计

2.1卡尔曼滤波器设计

卡尔曼滤波器是一种用于时变线性系统的递归滤波器。它以最小均方误差为最佳估计的原则，建立信号与噪声的状态空间模型。

设离散卡尔曼滤波的线性差分方程及测量方程如下[7]：

图1　PMSM矢量控制结构图

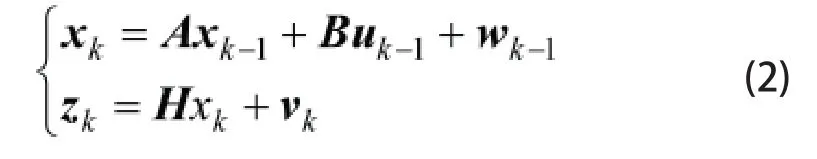
其中xk代表状态变量；zk代表观测变量；uk代表控制变量；变量wk和vk分别代表过程噪音和测量噪音，假设两者都是均值为零的高斯白噪声，且不相关。

卡尔曼滤波器分成两个过程：时间更新方程和测量更新方程。时间更新方程负责及时向前推算当前状态变量和误差协方差估计的值，称为先验估计。测量更新方程是将预先的估计值和实时测量值结合起来得出最优估计值，称为后验估计。

时间更新方程：

测量更新方程：

其中Kk为卡尔曼增益；R为测量噪声协方差矩阵。

已知永磁同步电机机械方程：

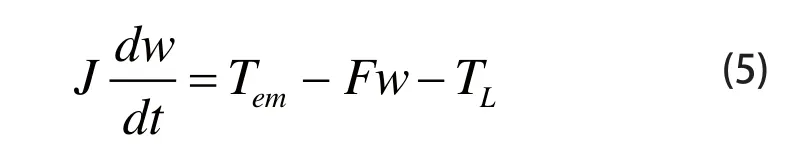
对于隐极式结构的电机而言，则电磁转矩为：

假设在恒转矩模式下运行，可以得出：

由式(5)～式(8)可以得到永磁同步电机连续系统的状态方程以及测量方程：

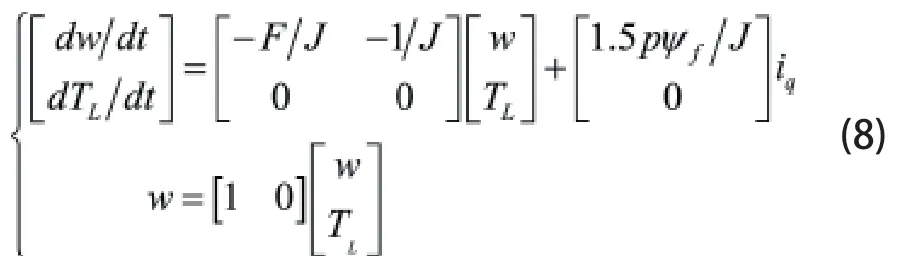
通常计算机在处理信号系统时，观测值是离散的。在满足离散化的基础上，得到离散状态方程表达式：

结合上述推倒公式可知，只要给出系统的初始值x(0)和初始误差p(0)，选择适当的矩阵Q、R，将永磁同步电机的实验参数代入方程中，经过多次的迭代计算，可以得到矫正的卡尔曼滤波增益值Kk，再根据此时刻的测量值y(k)，可计算出最优估计状态x(k)。

2.2位置滑模变结构的设计

滑动模态变结构是一种高速切换的反馈控制系统，通过控制量的切换迫使系统状态在一定特征下沿着滑模面滑动，运动轨迹呈现小幅度、高频率的上下反复运动。这种滑动模态是可以设计的，且与系统的参数及扰动无关[8]。由于滑模变结构调节器的设计对系统模型精度要求不是很高，在设计最外环的位置环时，将速度闭环（包含电流环）系统近似等效为一阶惯性环节，以此为基础设计出位置环滑模变结构控制器。

根据上述状态方程将其离散化，则离散系统状态方程：

选取位置环滑模切换函数为：

滑模变一般指数趋近律表达式为：

从而推导出离散指数趋近律：

由式(12)、式(15)结合可得：

假设滑模变结构可控条件CB≠0成立，可以得出滑模控制率为：

为了能够有效地消除离散滑模控制的抖振，采用带有边界层厚度的饱和函数sat(s)来替代理想滑模中的符号函数sgn(s)：

图2　位置环滑模结构控制器的结构图

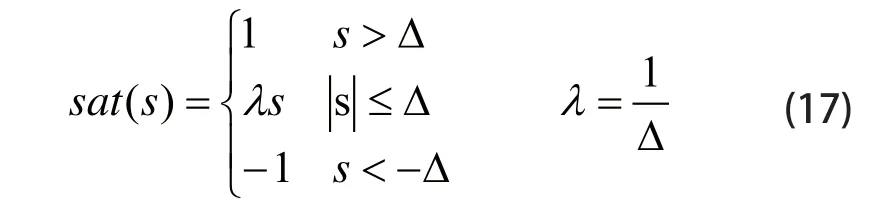
将已知矩阵A、B、C带入式(16)得出：

根据上述公式推导，位置环滑模变结构框图如图2所示。

3　实验仿真

仿真中永磁同步电机的主要参数如下：定子绕组电阻Rs=2.875Ω，电枢电感L=Ld=Lq=8.5mH，转子磁链Ψr=0.1688Wb，转动惯量J=0.0008kg/m2，极对数p=4。

在卡尔曼滤波观测器中，采样周期T1为0.1ms，状态变量初始值x0=[1 1]，滤波协方差初始值，R=0.001。

在位置滑模变结构中，采样周期Tc为0.5ms，c=20，k=15，ε=5。

在仿真实验中，先断开位置环，电机给定速度为1500r/min，0～0.15s时负载转矩为5N☒m，在0.15s时刻突加负载至20N☒m。由图3和图4比较可知，当负载转矩发生突变时，未加卡尔曼模块的电机速度下降幅度大，恢复到稳定转速时间长，而加卡尔曼模块的速度明显下降幅度较小，恢复稳定转速时间短。因此可以看出卡尔曼观测器通过转矩负载正反馈补偿稳定了转速，大幅度提高了电机的抗负载突变能力。由图5和图6比较，同时结合上述公式(6)，可以得知通过观测补偿机制大大提高了电流环中q轴反应时间和幅值，迅速弥补了负载转矩波动带来的影响。

图3　未加卡尔曼观测器的电机转速波形

图4　加卡尔曼观测器的电机转速波形

图5　未带卡尔曼的电磁转矩波形

图6　带卡尔曼的电磁转矩波形

后断开速度环，分别加上位置PID控制以及滑模变结构，构成完整的三环伺服控制系统，其中电机位置给定为8rad，负载转矩给定为5N☒m，仿真时间为0.5s。由图7和图8比较可知，PID控制实现的位置追踪出现超调现象，而滑模控制可以实现位置信号的准确跟踪，并且快速、无超调，使整个系统具有较高的跟踪精度和较好的动态性能。

图7　PID控制位置追踪波形

图8　滑模变控制位置追踪波形

4　结束语

针对永磁同步电机伺服系统的控制，本文给出了多算法控制的设计方案并进行了MATLAB/Simulink仿真。仿真结果表明，在外界干扰情况下，将卡尔曼滤波器应用到速度环，有效地稳定了转速，提高了抗负载突变能力；将滑模变结构应用到位置环，实现了位置的快速跟踪同时提高了跟踪精度。二者的有效结合，使系统具有很强的鲁棒性，同时发挥出良好的动态性能。

[1] 孙凯,许镇琳,盖廓,等.基于自抗扰控制器的永磁同步电机位置伺服系统[J].中国电机工程学报,2007,27(15)：43-46.

[2] 邵明玲,于海生.基于模糊RBF神经网络的永磁同步电机位置控制[J].青岛大学学报(工程技术版),2014,29(4)：27-31.

[3] 尹忠刚,张瑞峰,钟彦儒,等.基于抗差扩展卡尔曼滤波 器的永磁同步电机转速估计策略[J].控制理论与应用,2012,29(7)：921-927.

[4] 章玮,姚卫忠,梁文毅.基于卡尔曼滤波器的永磁同步电动机转速精确控制[J].微电机,2008,41(1)：4-6.

[5] 黄飞.永磁同步电机位置伺服控制的滑模控制[J].重庆交通大学学报(自然科学版),2011,30(4)：860-863.

[6] 李华德,李擎,白晶.电力拖动自动控制系统[M].北京：机械工业出版社,2008.9.

[7] 洪乃刚,等.电力电子和电力拖动控制系统的MATLAB仿真[M].北京机械工业出版社,2006

[8] Welch G,Bishop G.Introduction to the Kalman Filter [D].Chapel Hill：Department of Computer Science University of North Carolina,2006：2-6.

Permanent magnet synchronous motor servo control system based on multi-algorithms

LI Zhi-hong1, WU Lian-shun1, LI Yu-ping1, QIAN Chen-liang1, LIU Jie2

TP273

A

1009-0134(2016)07-0025-05

2016-04-05

李志宏（1970 -），男，副教授，本科，主要从事船舶自动化研究等。