一种改进的EEMD算法及其在滚动轴承故障诊断中的应用
李亚超, 刘 政, 马增强
(1.南车青岛四方机车车辆股份有限公司,山东 青岛 266111;2.石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043)
一种改进的EEMD算法及其在滚动轴承故障诊断中的应用
李亚超1,2, 刘 政2, 马增强2
(1.南车青岛四方机车车辆股份有限公司,山东 青岛 266111;2.石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043)
总体经验模式分解 (Ensemble Empirical Mode Decomposition, EEMD) 方法由于其自适应性和抗混叠的特性,在轴承故障诊断领域得到广泛应用。针对总体经验模式分解 (Ensemble Empirical Mode Decomposition, EEMD) 方法中参数难以准确获取的问题,提出了基于改进的EEMD分解和Teager能量算子的滚动轴承故障诊断方法。首先对故障信号进行预处理,自动获取EEMD方法中的加入白噪声大小和总体平均次数两个重要参数。之后对信号进行EEMD分解,得到若干个本征模态分量 (Intrinsic Mode Function, IMF),利用峭度准则选取其中峭度最大的分量并进行Teager能量算子解调,最后通过能量谱识别出滚动轴承的工作状态和故障类型。将该方法应用到滚动轴承仿真故障数据和实际数据中,实验结果表明,该方法可有效提取滚动轴承故障特征频率信息,验证了所提方法的可行性。
滚动轴承;EEMD;Teager能量算子;故障诊断
0 引言
滚动轴承是旋转机械中应用最为广泛、也是最容易损坏的零件之一。据统计,在使用滚动轴承的旋转机械中,约有 30% 的机械故障由滚动轴承引起,滚动轴承质量的好坏对机械设备工作状况有很大影响。因此,对滚动轴承的故障诊断具有重要的意义。
在滚动轴承早期故障信号中,由于噪声污染严重,导致低频段特征频率极其谐波特征频率极其微弱。在诸多的滚动轴承故障诊断方法中,共振解调技术由于其准确性和易用性得到了大量的应用,侯丽娴[1]等通过共振解调法提取到了微弱的轴承故障特征频率,但该方法中带通滤波器的参数的设置需要丰富的专业知识和大量的经验积累提前确定。王天金[2]等提出了将Teager能量算子与时频分析相结合的方法避免了共振解调方法需要人工确定参数的缺点,但对噪声的抑制效果不太理想。左庆林[3]等将经验模式分解 (Empirical Mode Decomposition, EMD) 和共振解调结合,增强了对噪声的抑制效果,但依然存在带通滤波器的参数需要提前确定的问题。李辉[4-5]等将EMD和Teager能量算子相结合完成了滚动轴承的故障诊断,克服了带通滤波器的参数需要提前确定的缺点,然而EMD存在模态混叠等缺点,因此,Huang[6]提出了EEMD算法。王晓龙[7]等提出了基于EEMD和Teager能量算子解调的故障诊断方法,并将其应用于滚动轴承的故障诊断中,实现了故障类型识别。虽然克服了EMD模态混叠的缺点,但EEMD方法中的参数 (加入白噪声的幅值系数K和总体平均次数M) 设置缺乏理论依据,选取困难。陈略[8]等分析了不同幅值系数的白噪声对EEMD分解的影响规律,提出了自适应EEMD方法,实现了EEMD分解方法参数的自适应选取并应用到心电信号处理中,验证了方法的有效性。
在上述理论的基础上,本文针对滚动轴承早期故障信号的特点,提出了基于改进的EEMD和Teager能量算子的滚动轴承故障诊断方法,该方法先对故障信号进行预处理来确定EEMD的参数,根据确定的参数对信号进行EEMD分解,通过峭度准则选取峭度最大的分量并做Teager能量算子解调,得到能量谱,判断故障信息。通过对仿真和实测数据的分析,证明了该方法的有效性。
1 EEMD算法基本原理及其不足
EEMD算法是一种噪声辅助的数据分析方法,十分巧妙地利用了高斯白噪声频率分布均匀的统计特性,加入白噪声后,改变了信号极值点的特性,将使信号在不同尺度上具有连续性,促进抗混分解,避免模态混叠。EEMD实质上把一个全体测试的均值定义为真是的IMF分量,每个分量都包含了信号和有限幅值的白噪声,能够明确分理出各个时间尺度。具体流程如下:
(1)初始化EMD执行的总次数M,加入白噪声的幅值比值系数K,令m=1。
(2)对所添加白噪声的信号进行第m次分解。
①为待x(t)分解信号加上一个给定幅值的白噪声
(1)
式中,nm(t)、xm(t)分别代表第m次分解所添加的白噪声和加噪后的信号。
②使用EMD分解加噪信号xm(t),得到L个IMF分量。
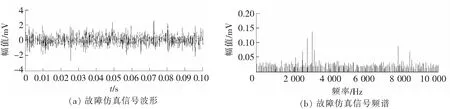
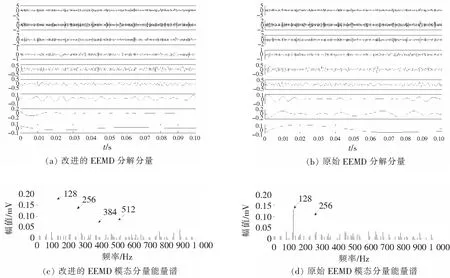
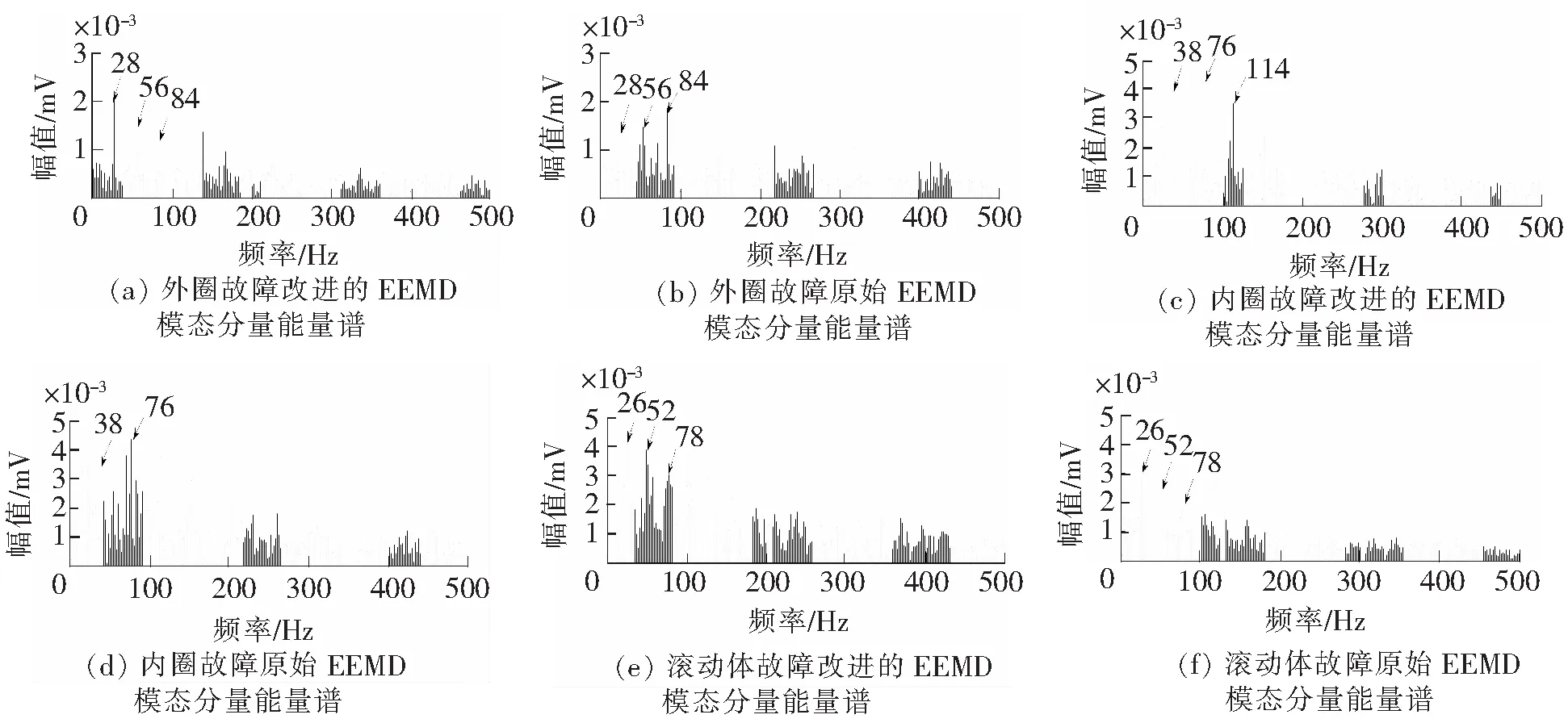
③如果m (3) 计算M次分解后每一个IMF的总体平均 (2) 式中,ai,m为第m次分解得到的第i个IMF。平均得到的IMFi,即第i个IMF的最终结果。 EEMD方法的提出,较好地解决了模态混叠的问题,但其效果依赖于加入白噪声的大小与总体平均的次数。加入白噪声的目的是平滑异常事件,使信号极值点的分布更加均匀,而不同的K值对极值点分布均匀性的影响存在差异,当所加白噪声使信号的极值点分布最为均匀时,EEMD的分解精度达到最高。同时,总体平均次数M的增大可以减小分解误差和提高分解精度,但当M增大到一定程度后,对分解误差和精度已无明显改善。原始EEMD方法中这两个参数都需要人为按照经验设定,针对不同的信号缺乏可靠性,同时破坏了EEMD方法的自适应性,因此建立一种能根据分析信号的不同特点自动获取加入白噪声大小与总体平均次数的自适应EEMD方法,对于分析非线性、非平稳信号具有重要意义。 2.1 改进的EEMD算法原理 为了有效避免EMD中模态混叠的现象,同时为了保护信号中的有用信息,在EEMD方法中加入的白噪声须满足以下两个前提条件[9]: (1)加入的白噪声应不影响信号高频成分的极值点分布;(2)加入的白噪声应改变低频成分的极值点间隔分布,使得低频成分的极值点间隔减小,使其分布均匀,减小三次样条函数的拟合包络求局部均值的误差。要满足以上两个条件,其关键点就是对于任何不连续的信号,如何确定一个在EEMD方法中有效的加入白噪声的可依据准则。 Wu et al[10]研究了EEMD方法中加入白噪声的幅值比值系数与集成次数选择之间的关系,研究表明,噪声对于分解结果的影响e、K与M的关系满足 (3) 根据式(3)并根据EEMD的前提条件,本文提出了一种加入白噪声的自适应准则,其具体实现过程描述如下: (1)计算输入信号x(t)的幅值标准差 (4) 式中,ux为x(t)平均值;N为数据长度。 (2)对x(t)进行EMD分解,取第一个分量c1为高频分量,计算c1的幅值标准差 (5) (3)计算信号中高频成分幅值标准差eh与原始信号幅值标准差e0的比值系数,即 (6) (7) 式中,en为白噪声的幅值标准差。 (6)根据K和M进行EEMD分解得到IMF分量。 2.2 基于改进的EEMD分解和Teager能量算子的滚动轴承故障特征提取 对于离散时间信号,Teager能量算子只需要3个样本数据就可以计算任意时刻的信号源能量,因此,它对于信号的瞬时变化具有良好的时间分辨率,能够检测信号中的瞬态成分[11]。基于Teager能量算子的特性,本文将改进的EEMD分解和Teager能量算子相结合进行滚动轴承故障诊断,诊断流程如图1所示,实现步骤如下: (1)设定期望的信号分解相对误差e为1%,对原始信号进行EMD分解,选取IMF1作为高频成分,进而确定EEMD算法中的白噪声大小en和总体平均次数M; (2)根据步骤 (1) 的结果对信号进行改进的EEMD分解,对得到的IMFs进行峭度计算; (3)选取其中峭度最大的IMF分量,对其进行Teager能量算子解调; (4)根据步骤(3)得到的能量谱,确定滚动轴承工作状态和故障类型。 图1 基于改进的EEMD的滚动轴承故障诊断方法流程 为验证本文算法的有效性和可行性,使用单位周期冲击序列,并向其中添加强烈白噪声来模拟滚动轴承的单点故障,仿真信号如下 (8) 式中,幅值A=1;衰减系数k为800;系统共振频率ωr=2×π×1 000;u(t)为单位阶跃函数;设定信号的故障特征频率fr=128;滚珠和滚道之间微小滑动对故障特征频率的影响因子τi为0.01/fr~0.02/fr的随机数。采样频率为25 600Hz,n(t)为白噪声,加入信噪比为-20 dB的白噪声。冲击信号波形、故障仿真信号的波形及频谱如图2所示。 图2 仿真信号的波形及频谱 利用本文方法对仿真信号进行分析,首先确定加入白噪声幅值为K=0.097和总体平均次数为M=96。原始信号经过本文方法处理后得到9个IMF分量如图3(a),求取8个IMF分量的峭度值如表1,可以看出IMF2的峭度最大,对其进行Teager能量算子解调如图3(c) 。 表1 仿真信号改进的EEMD算法IMF分量的峭度值 图3 仿真信号诊断结果对比 为了验证本文方法的优势,作为对比利用原始EEMD (噪声的幅值为K=0.01和总体平均次数为N=100) 结合Teager能量算子对上述仿真信号进行处理,并对其中峭度最大的分量做解调处理。对比图5(c)、图5(d),在故障频率128Hz及其倍频的诊断结果上,本文方法结果主频幅值达到0.176mV,谐波为5阶,能够更好地体现出低频信号的周期特性,能量谱特征频率及其倍频谱线幅值明显,证明了本文方法的有效性。 图4 QPZZ-Ⅱ旋转机械故障试验平台 为了验证本研究方法在滚动轴承故障特征提取中的有效性,采用江苏千鹏诊断工程有限公司的QPZZ-Ⅱ旋转机械振动故障试验平台进行试验分析,如图4。采用N205EM轴承故障模型作为样本进行分析,该轴承参数:圆柱滚子数z=13,节圆直径D=38.5 mm,滚子直径d=7.5 mm,接触角为0°。实验中,信号采样频率为25 600 Hz,采样点数为20 480,转速为317 r/min。由滚动轴承故障特征频率理论计算可得外圈故障特征频率为27.55 Hz、内圈故障特征频率为40.64 Hz、滚动体故障特征频率为25.9 Hz。分别用原始EEMD方法和改进EEMD方法对滚动轴承外圈、内圈和滚动体故障进行分析,结果如图5所示。 图5 滚动轴承故障信号诊断结果对比 故障类型自适应参数KM原始方法主频幅值改进方法主频幅值(改进/原始)/%外圈故障0.06451.372.15159内圈故障0.09993.654.05111滚动体故障0.08752.754.25155 从上述结果中可以看出,针对滚动轴承的外圈、内圈和滚动体故障,相比于原始EEMD方法故障特征频率的主频幅值,改进的EEMD受噪声影响较小,Teager能量谱中故障特征频率幅值分别达到了原始信号的159%、111%、155%,谐波次数更高。综上,原始EEMD方法虽然可以提取出故障特征频率,但其他背景噪声干扰成分明显。改进的EEMD方法中能量谱主频幅值较高,噪声影响较小,凸显了故障特征。 滚动轴承早期故障特征信号微弱,特征提取相对困难,本文针对EEMD算法中参数难以准确获取的问题,提出了利用改进的EEMD来分析轴承早期故障信号,可有效提取出微弱特征频率信息,实现轴承状态的准确判别,仿真和实测数据分析表明,与原始EEMD相比,改进的之后的EEMD方法结合Teager能量算子解调的提取效果更直观明显,噪声抑制效果更好,适合用于滚动轴承的精确故障诊断。 [1]侯丽娴,杨绍普,刘永强,等.基于共振解调的铁路货车轴承故障诊断[J].石家庄铁道大学学报:自然科学版,2013,26 (4) :47-51. [2]王天金,冯志鹏,郝如江,等.基于Teager能量算子的滚动轴承故障诊断研究[J].振动与冲击,2012,31 (2):1-5. [3]左庆林,马怀祥.基于EMD分解和共振解调的滚动轴承故障诊断研究[J]. 石家庄铁道大学学报:自然科学版,2014,27 (3) : 59-64. [4]李辉,郑海起,杨绍普.基于EMD和Teager能量算子的轴承故障诊断研究[J].振动与冲击,2008,27 (10):15-22. [5]李辉,郑海起,唐力伟.基于EMD和Wigner分布的轴承故障诊断研究[J].石家庄铁道学院学报,2005,18(2):10-14. [6]Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1 (1):1-41. [7]王晓龙.基于EEMD和Teager能量算子解调的故障诊断研究[J].电力科学与工程,2013,29 (3):18-22. [8]陈略,唐歌实,訾艳阳,等.自适应EEMD方法在心电信号处理中的应用[J].数据采集与处理,2011,26 (5): 361-366. [9]陈略,訾艳阳,何正嘉.总体平均经验模态分解与1. 5维谱方法的研究[J].西安交通大学学报, 2009, 43(5): 94-98. [10]Wu Zhaohua, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method [J]. Proceedings Royal Society of Lond, 2004, 460: 1597-1611. [11]Potamianos A, Maragos P. A comparison of the energy operator and Hilbert transform approaches for signal and speech demodulation [J]. Signal Processing,1994, 37(1): 95-120. Rolling Bearing Fault Feature Extraction Based on Modified EEMD and Teager Energy Operator Li Yachao1,2, Liu Zheng2, Ma Zengqiang2 (1.CSR Qingdao Sifang Co. LTD., Qingdao 266111, China;2.School of Electrical and Electronics Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China) With its adaptability and anti-aliasing, Ensemble Empirical Mode Decomposition (EEMD) is used widely in rolling bearing fault diagnosis. In order to solve the problem that the parameters of ensemble empirical mode decomposition(EEMD) is difficult to obtain, a method for fault diagnosis of rolling bearing based on modified EEMD and Teager energy operator is proposed. Firstly, the fault signal is preprocessed, the added white noise magnitude and the ensemble times is obtained. Then the fault signal is decomposed into several intrinsic mode function (IMF) by modified EEMD, and the IMF of biggest kurtosis is selected with Kurtosis Criterion and demodulated into Teager energy spectrum with Teager energy operator. Finally, the working status and fault type of rolling bearings is identified through the energy spectrum. The proposed method is applied to simulated signals and actual signals. The results show that the method could extract the weak feature frequency information of incipient fault of rolling bearing effectively. rolling bearing;EEMD;Teager energy operator;fault diagnosis 2015-09-24 责任编辑:刘宪福 10.13319/j.cnki.sjztddxxbzrb.2016.04.11 国家自然科学基金 (11227201;11372199;51208318) 李亚超(1990-),男,硕士研究生,主要从事滚动轴承故障诊断的研究。E-mail:z364812@sina.com李亚超,刘政,马增强.一种改进的EEMD算法及其在滚动轴承故障诊断中的应用[J].石家庄铁道大学学报:自然科学版,2016,29(4):66-71. TH165+.3 A 2095-0373(2016)04-0066-062 基于改进的EEMD算法和Teager能量算子的滚动轴承故障特征提取
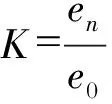
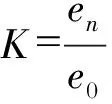

3 仿真信号分析

4 实验分析


5 结论

