一个能量与位势相依的二阶谱问题及其相关的发展方程族

张瑞君, 刘亚峰

(1.河北工业大学 理学院， 天津 300401；2.石家庄铁道大学 数理系，河北 石家庄 050043)



一个能量与位势相依的二阶谱问题及其相关的发展方程族

张瑞君1, 刘亚峰2

(1.河北工业大学 理学院， 天津 300401；2.石家庄铁道大学 数理系，河北 石家庄 050043)

本文将研究一个二阶谱系及相关的非线性发展方程及其Hamilton系统，利用Lax对非线性化方法，讨论经典力学的Jacobi-Ostrogradsky坐标，得到Bargmann约束下完全可积的 Hamilton系统，通过Bargmann约束，从而给出发展方程族解的对合表示。

谱问题； Lax对非线性化；Bargmann约束；可积系统

0 引言

非线性发展方程与有限维完全可积Hamilton系统之间的关系是数学物理研究的一个十分重要的内容。Lax对非线性化[1]是一个有效的获得有限维可积系统的方法，近年来被广泛用于求解非线性发展方程[2-4]，特别是孤子方程。本文研究一个新的二阶谱问题,得到一类HD型非线性发展方程族。通过将Lax对非线性化方法获得有限维Hamilton系统，并证明此系统在Liouville意义下的完全可积，进而由其Bargmann约束给出非线性发展方程解的表示。

1 谱问题及对应的发展方程族及Lax表示

讨论二阶线性谱问题

(1)

式中，u=u(x,t),v=v(x,t)为谱问题的位势函数；λ,φ分别为特征值及对应的特征函数。

在基础空间Ω=(-∞,+∞)上讨论谱问题(1)，假设u,ν,φ及其导数在x→±∞时速降。

命题1 (1)如下二阶谱问题构成完整谱系

(2)

(2)若φ,ψ是谱系(2)的特征值λ所对应的特征函数，则

(3)

设谱问题(1)的辅谱问题为φtm=wmφ，其中

(4)

令gj=(bj，bj+1)T，j=-1,0,1,2，…,m,则由相容性条件φxxt=φtxx，得如下递推关系

(5)

其中

(6)

直接计算可知

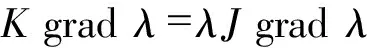
(7)

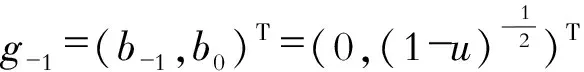
并由(5)得到递推序列{gj,j=1,2,…}。

定理2 在等谱(λt=0)条件下，非线性发展方程族为

(8)

对应的Lax对为

(9)

显然，这是一个HD型非线性发展方程族。特别，当m=0时，发展方程为

(10)

当m=1时，发展方程为

(11)

2 Bargmann系统与Hamilton正则系统

设谱系(2)的N个不同的特征值为λ1<λ2<…<λN,φj,ψj为对应于λj，j=1,2,…,N的特征函数，

令Λ=diag(λ1,λ2,…,λN),φ=(φ1,φ2,…,φN)T,ψ=(ψ1,ψ2,…,ψN)T。

命题3 设Gj=(<Λjφ,ψ>,<Λj+1φ,ψ>)，则

KGj=JGj+1。

令g0=G0，构造Bargmann约束[1]

(12)

由此，谱系(2)等价于如下Bargmann系统

(13)

现在寻找Bargmann系统(13)对应的Hamilton系统的Jacobi-Ostrogradsky坐标。

定义Lagrange函数

(14)

其中

(15)

命题4 Bargmann系统(13)等价于如下Euler-Lagrange方程

(16)

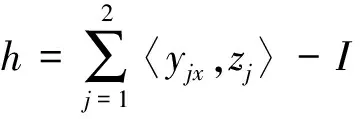
则y1,y2,z1,z2满足如下方程[5]

(17)

由文献[4]的方法，得

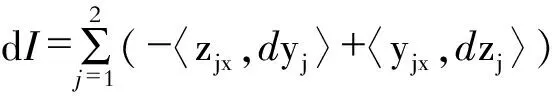
若取y1=φ，y2=ψ,直接计算得z1=ψx+Λψ,z2=φx-Λφ。

构造Jacobi-Ostrogradsky坐标如下

(18)

在坐标系(18)下，Bargmann约束化为

(19)

由此Bargmann系统(13)等价于如下Hamilton正则系统

(20)

此时

(21)

3 Hamilton系统的完全可积性

在Bargmann约束(19)和Jacobi-Ostrogradsky坐标(18)下, 发展方程族的Lax对(9)非线性化为如下矩阵形式[1,4]

(22)

其中

(23)

定理5 在Bargmann约束条件(19)下，发展方程族Lax对(9)等价于如下Hamiltom正则方程[4,7]

(24)

其中Hamiltom函数为(21)式，hm为

(25)

令[6]

(26)

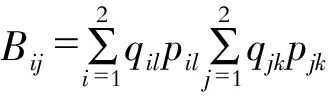
命题6

(27)

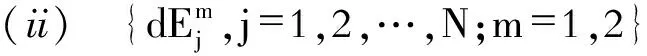
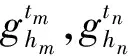
证明：由(27)式直接计算得{Υμ,Υλ}=0 ，{hm,hn}=0,m,n=0,1,2,…。

所以{h,hm}=0,m=0,1,2,…

由Arnold定理[5]，Hamiltom系统(24)是完全可积系，且Hamiltom相流可换。

定理8 设(q1,q2,p1,p2)满足Hamiltom系统(24)，则式(19)

u=1-〈Λq1,p2〉-2〈Λ2q1,p2〉〈Λq1,p2〉-3

为非线性发展方程族(8)的对合解[2,4]。

4 结论

本文主要研究了H-D型非线性发展方程族的Lax对，根据谱问题的位势函数与特征函数之间的约束关系，可得到Liouvile意义下的完全可积系统，进而利用完全可积的Hamilton系统的对合解表示发展方程的解。

[1]曹策问.AKNS方程族的Lax方程组的非线性化[J].中国科学A，1989(7):701-707.

[2] 耿献国，曹策问.一个Bargmann系统与一类演化方程解的对合表示[J].数学年刊，1992， 13A(s):92-98.

[3]CaoCewen，WuYongtang,GengXianguo．RelationbetweentheKadometsev-Petviashviliequationandtheconfocalinvolutivesystem[J]．J.Math.Phys，1999，40(8):3948-3969．

[4]GuZhuquan.TheNeumannsystemforthethird-ordereigenvalueproblemsrelatedtotheBoussinesqequation[J].ILNuovoCimento, 2002,117(6)：615-631.

[5]ArnoldVI．MathematicalMethodsofClassicalMechanics[M]．Berlin：Springer, 1978．

[6] 谷超豪,曹策问，李翊神．孤立子理论与应用[M]．杭州：浙江科学技术出版社,1990．

[7]ZhaoYe，GuZhuquan，LiuYafeng．TheNeumannsystemforthe4th-ordereigenvalueproblemandconstraintflowsofthecoupiedKdV-typeequations[J].Eur.Phys.J.Plus，2012，127：77．

The Second-order Spectral Problem of Energy Depended on Potential and Hierarchy of Evolution Equations

Zhang Ruijun1, Liu Yafeng2

(1.School of Science,Hebei University of Technology，Tianjin 300401，China；2.Department of Mathematics and Physics, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

In this paper, the nonlinear evolution equation and the Hamilton system related to a second-order spectral problem are studied. Using the nonlinearization approach of Lax pairs, the Jacobi-Ostrogradsky coordinates of classical mechanics is discussed. Finally the completely integrable Hamilton system can be obtained in the Bargmann constraint condition, and the involutive solutions of the evolution equations are given.

spectral problem;ninlinearization of Lax pairs;Bargmann system;integrable system

2016-04-05 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2016.04.18

张瑞君(1991-),女,硕士研究生,主要从事基础数学的研究。E-mail:952564326@qq.com

O175.9

A

2095-0373(2016)04-0105-04

张瑞君,刘亚峰.一个能量与位势相依的二阶谱问题及其相关的发展方程族[J].石家庄铁道大学学报:自然科学版,2016,29(4):105-108.