剪切变形对基桩PΔ效应的影响

李微哲,娄平

(1.中南大学 土木工程学院 长沙 410012；2.中煤科工集团 重庆设计研究院有限公司，重庆400016)



李微哲1,2,娄平1

(1.中南大学 土木工程学院 长沙 410012；2.中煤科工集团 重庆设计研究院有限公司，重庆400016)

1 计入剪切变形的PΔ效应杆单元

假定单元节点的弯矩逆时针方向为正，顺时针方向为负；节点剪力、轴力方向与坐标轴方向相为正。则根据材料力学原理,单元节点i、j的弯矩与节点位移关系如下：

(1)

式中:Mi、vi、Mj、vj分别为节点i的弯矩、位移和节点j的弯矩和位移;z为单元长度方向坐标;E为计算弹性模量。

对节点i进行平衡弯矩分析，其弯矩平衡方程为

(Mi+Mj)+FQj(zj-zi)-FNj(vj-vi)=0

(2)

对节点j进行平衡弯矩分析，其弯矩平衡方程为

(Mi+Mj)-FQi(zj-zi)+FNi(vj-vi)=0

(3)

将式(1)代入式(2)得

FNj(vj-vi)=0

(4)

将式(1)代入式(3)得

FNi(vj-vi)=0

(5)

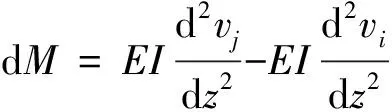
(6)

(7)

1.2 剪切变形和弯曲变形位移模式

假定考虑剪切变形的杆单元水平位移模式为

v=vb+vs

(8)

vb(z)=a0+a1z+a2z2+a3z3

(9)

vs=vsL+vsV=a4+a5z

(10)

式中:v为单元总水平位移;vb弯曲变形引起的水平位移;vs为剪切变形引起的水平位移;vsL为水平力剪切变形产生的水平位移;vsV为竖向力径向剪切分力剪切变形产生的水平位移。

则仅考虑弯曲变形时，单元i节点(Z=0)和单元j节点(z=l)的水平位移和转角如下：

(11)

式中:l为单元长度;a0、a1、a2、a3为待定系数;vib、vjb、φib、φjb为仅考虑弯曲变形时单元节点i和j的水平位移和转角。

根据式(11)，可将a0、a1、a2、a3待定系数表达成vib、φib、vjb、φjb的表达式为

(12)

将式(12)代入式(9),可得单元弯曲变形水平位移函数为

(13)

则仅考虑剪切变形时，单元i节点(Z=0)和单元j节点(z=l)的水平位移和转角为

(14)

将式(14)代入式(10),则单元剪切变形水平位移函数为

(15)

依材料力学和图1假定，水平剪力、竖向力径向剪切分力产生的剪切变形计算为

(16)

(17)

(18)

式中:FQ为单元剪力;k为形状剪切系数，对矩形截面取1.2，对圆形截面取10/9，G为计算剪切模量;visL、vjsL、φisL、φjsL分别为水平力剪切变形在单元i、j节点产生的水平位移和转角;visV、vjsV、φisV、φjsV分别为竖向力径向剪切分力剪切变形在单元i、j节点产生的水平位移和转角。

1.3 单元刚度矩阵方程

因剪切变形引起的转角在节点不连续，则

(19)

根据式(5)、式(8)和式(10)可得

(20)

则联合式(1)、(4)和式(13)，可得单元剪力为

(21)

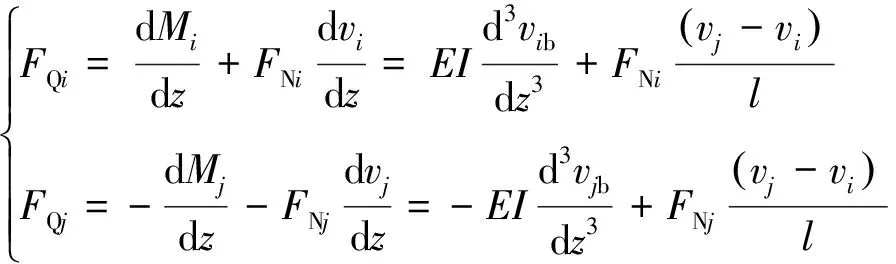
(22)

将式(13)代入式(22)可得单元节点剪力为

(23)

(24)

将式(13)、(19)代入式(1)可得单元节点弯矩为

(25)

(26)

将式(16)代入式(23)可得计入剪切变形后单元节点位移关系为

(27)

或

(28)

将式(17)代入式(23)可得仅计入水平力剪切变形而忽略竖向力径向剪切分力剪切变形时的单元节点位移关系如下：

(29)

由式(18)可得仅计入竖向力径向剪切分力剪切变形而忽略水平力剪切变形时的单元节点位移关系如下：

(30)

将式(27)代入式(23)可得同时计入水平力剪切变形和竖向力径向剪切分力剪切变形时，单元节点剪力、弯矩与节点总水平位移、弯曲变形引起的转角之间关系为

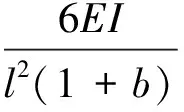
(31)

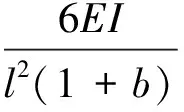
(32)

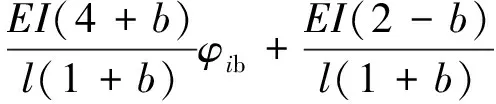
(33)

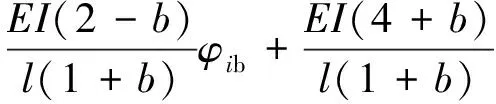
(34)

(35)

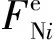
(36)

(37)

(38)

(39)

1.5 考虑剪切变形时单元节点转角的计算

(40)

(41)

(42)

式中：φi为节点i转角；vi-1vi、vi+1分别为i-1节点、i节点和i+1节点的位移，式(40)应用于一般节点，式(41)或式(42)适用于端节点。

1.6 单元内力求解

在小变形情况下，当已知节点位移时，可按式(35)～(37)计算单元节点内力时，剪力结果未计入竖向力径向剪切分力结果。如需在小变形情况下计入竖向力径向剪切分力影响，在计入剪切变形影响、仅计入水平力剪切变形影响、仅计入竖向力径向剪切分力剪切变形影响时应分别按式(26)、 (27) 、(28)计算单元节点内力。

(43)

(44)

(45)

式(43)～(45)分别由式(35)～(37)演化而来，主要是在反算单元节点剪力时已计入了小变形情况下竖向力因倾角而产生的径向剪切分力。式(43)～(45)的剪力项分别减去式(35)～(37)对应的剪力项即可得竖向力因倾角而产生的径向剪切分力。

某支座高h=0.3 m，直径d=850 mm，剪切模量G=2 MPa，抗压弹性模量E=5 000 MPa，竖向力FN= 15 000 kN，水平力FH=180 kN。

支座受力如图2，支座顶水平位移由剪切变形Vs和弯曲变形Vm组成，但剪切变形远大于弯曲变形，且与支座高度h同数量级，为典型的大剪切变形构件；支座底部总弯矩由竖向力偏心弯矩和水平力矩组成，竖向力偏心弯矩往往极显著，且远大于水平力矩。支座偏心受压后其竖向抗压刚度会随之变化，其弯曲变形会出现一定的非线性，本文暂时忽略此影响，并假定其抗压弹模不变。

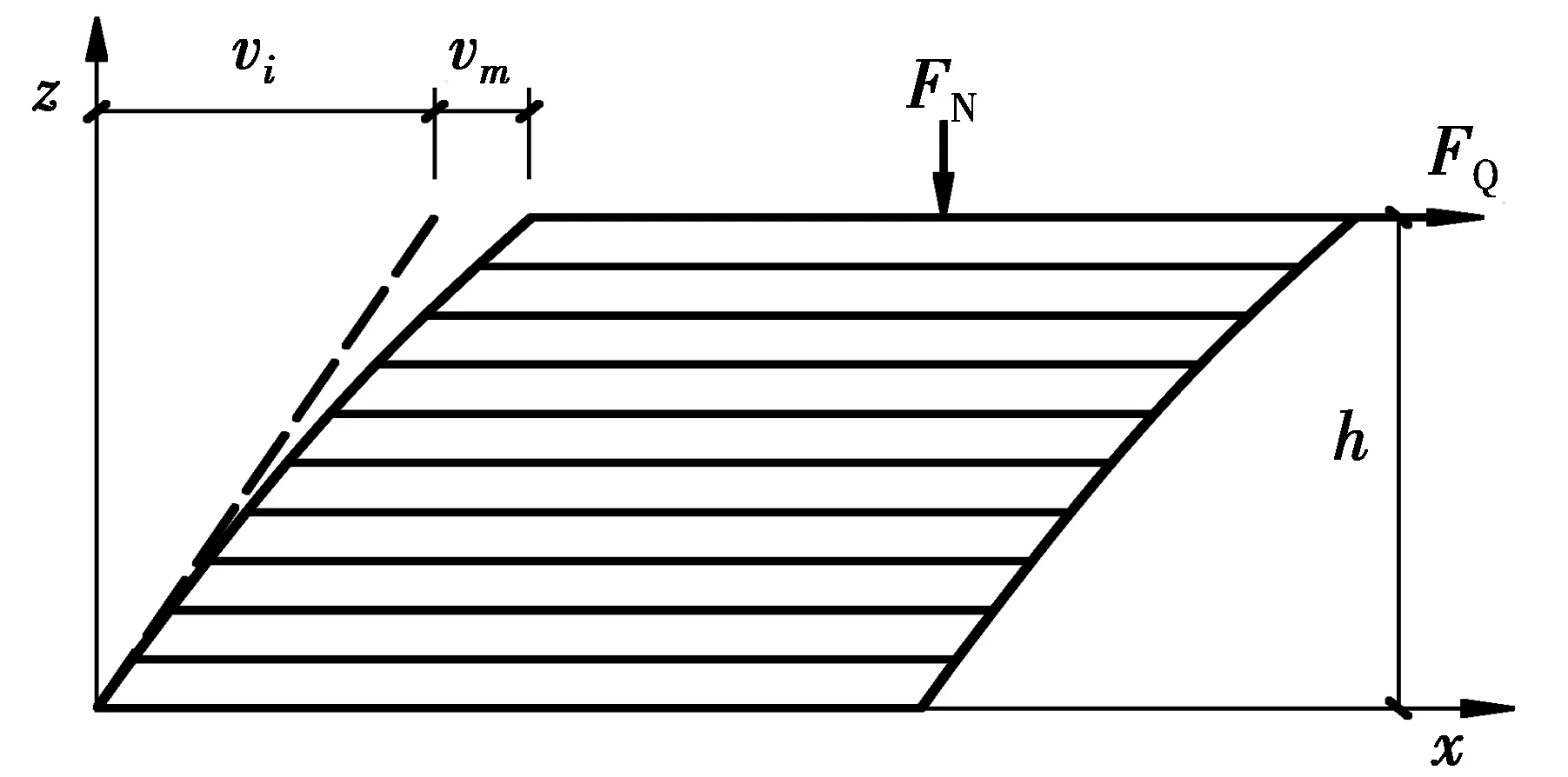
图2 支座受力示意图Fig.

表1 支座位移内力结果

Table1 Deformation and moment of bearing element

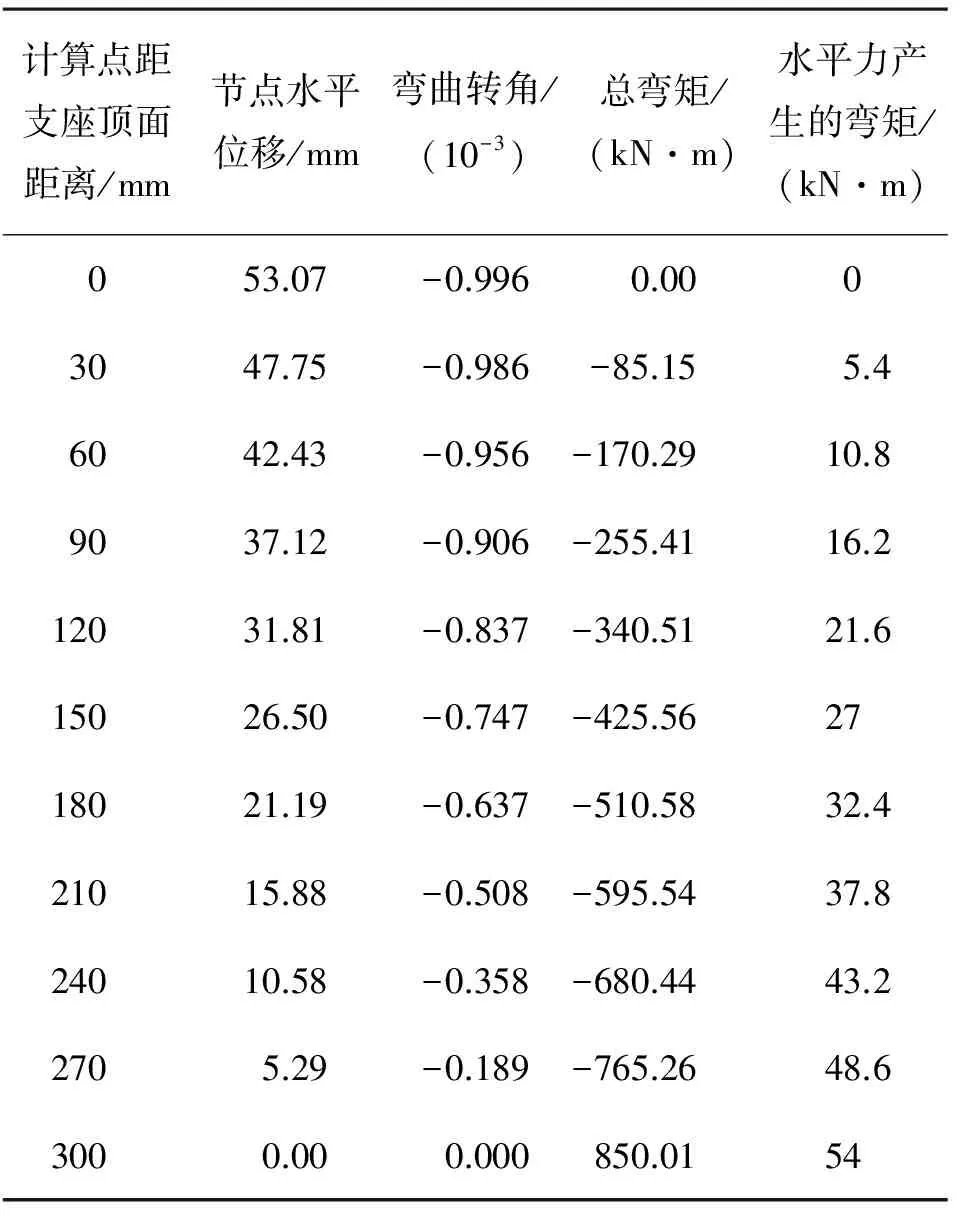
计算点距支座顶面距离/mm节点水平位移/mm弯曲转角/(10-3)总弯矩/(kN·m)水平力产生的弯矩/(kN·m)053．07-0．9960．0003047．75-0．986-85．155．46042．43-0．956-170．2910．89037．12-0．906-255．4116．212031．81-0．837-340．5121．615026．50-0．747-425．562718021．19-0．637-510．5832．421015．88-0．508-595．5437．824010．58-0．358-680．4443．22705．29-0．189-765．2648．63000．000．000850．0154

3 支座基桩共同作用算例二

某桥梁基桩[1,7,9]，冲刷线以上桩长30.212 m，其中l1=8.012 m，d1=1.8 m，E1=1.933 3×104MPa；l2=22.2 m，d2=2.2 m，E2=1.8×104MPa；在冲刷线以下桩长l3=42.8 m，d3=2.2 m，E3=1.8×104MPa；地基比例系数m=10 000 kN/m3，竖向荷载Fz=9 102.2 kN，水平荷载Fx=165 kN。设墩顶支座同算例一，且基桩剪切模型G=0.4E。

支座基桩受力如图3，支座顶水平位移由基桩水平位移Vp和支座自身水平变形Vb组成；且二者同数量级。基桩顶荷载除了上部结构传递的竖向力FN和水平力FQ外，还有竖向力因支座自身变形而产生的偏心弯矩FN·Vb，因竖向力和支座变形均很大，因此偏心弯矩不能忽略。

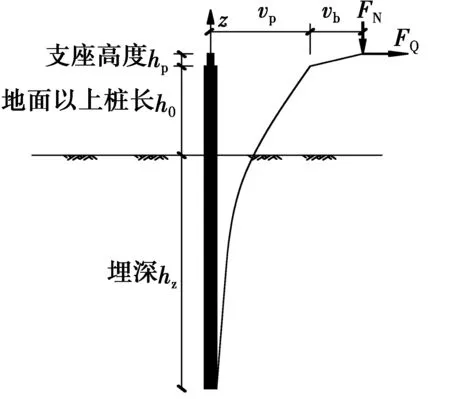
图3 支座基桩受力示意图Fig.

将支座划分了2个杆单元，其单元刚度矩阵方程采用式(36)；基桩划分了731个杆单元，在忽略和计入桩身剪切变性影响情况下其单元刚度矩阵方程分别采用 (38)和式(35)；并用自编MATLAB有限元程序计算，结果如表2和图4。

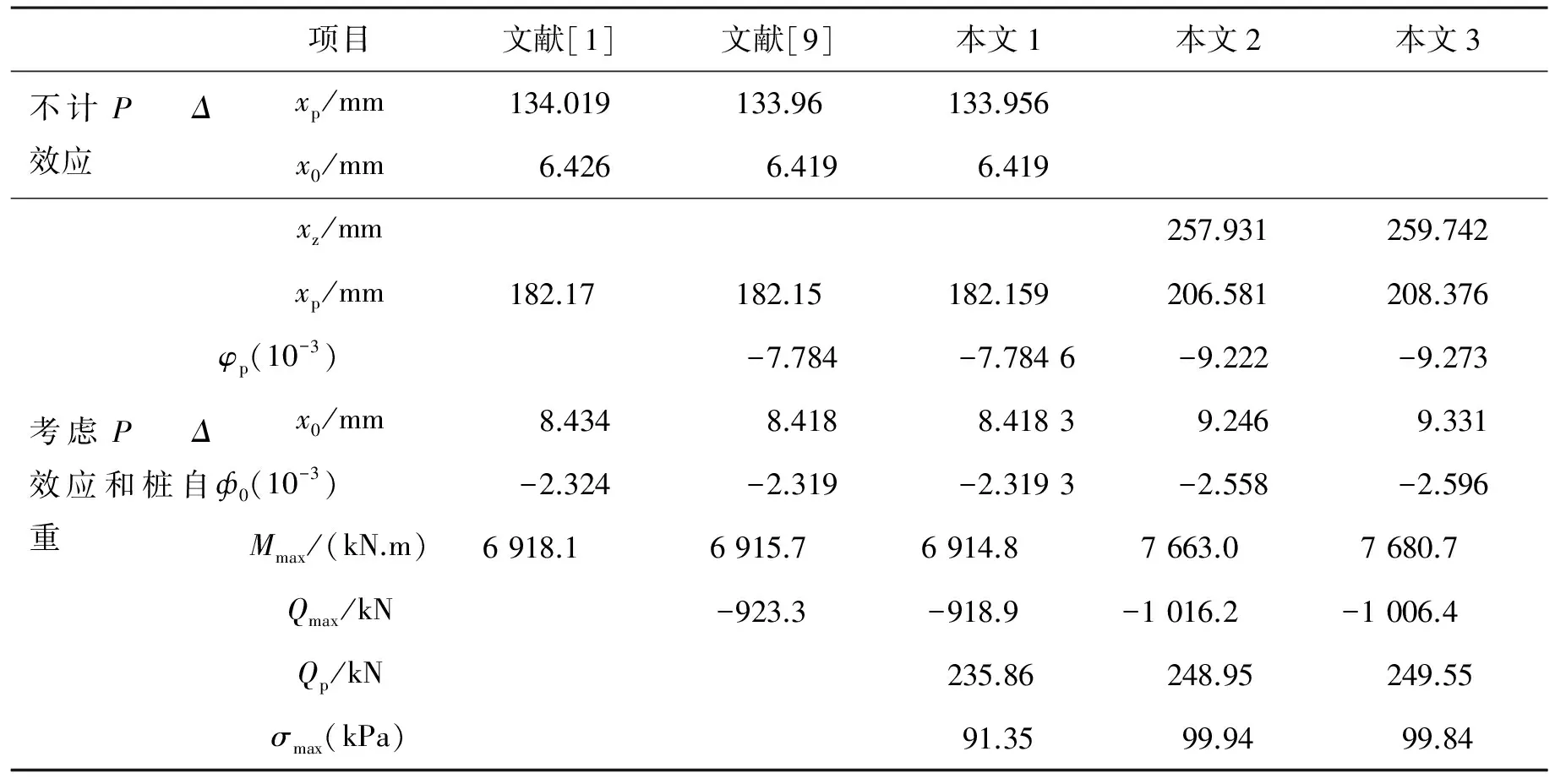
项目文献[1]文献[9]本文1本文2本文3不计PΔ效应考虑PΔ效应和桩自重xp/mm134．019133．96133．956x0/mm6．4266．4196．419xz/mm257．931259．742xp/mm182．17182．15182．159206．581208．376φp(10-3)-7．784-7．7846-9．222-9．273x0/mm8．4348．4188．41839．2469．331ф0(10-3)-2．324-2．319-2．3193-2．558-2．596Mmax/(kN．m)6918．16915．76914．87663．07680．7Qmax/kN-923．3-918．9-1016．2-1006．4Qp/kN235．86248．95249．55σmax(kPa)91．3599．9499．84

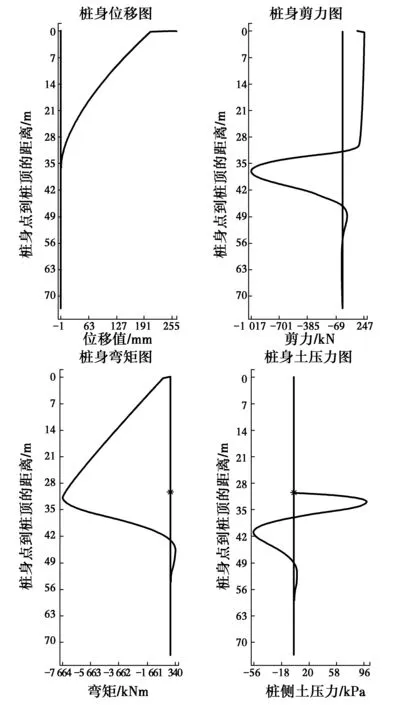
图4 支座和基桩PΔ效应的内力位移分布图(忽略桩身剪切变形影响)Fig.4 Distribution of internal force, displacement and soil pressure for pile and bearing while shear

4 结论

[1] 赵明华.轴向和横向荷载同时作用下的桩的计算[J].湖南大学学报,1987,14(2):68-81. ZHAO M H. The calculation of piles under simultaneous axial and lateral loading [J]. Journal of Hunan University, 1987, 14(2):68-81.

[2] 横山兴满.桩结构物的计算方法和计算实例[M]. 唐业清，吴庆荪.译.北京:人民交通出版社，1981. YOKOYAMA.Calculation method and cases of pile foundation [M]. Translated by Tang Yeqing & Wu Yisun. Beijing . China communication press, 1981. (in Chinese)

[3] 李微哲,赵明华,单远铭,等. 倾斜偏心荷载下基桩内力位移分析[J].中南公路工程，2005, 30(3) : 53-57. LI W Z, ZHAO M H, SHAN Y M, et al. Analysis of single pile under eccentric and inclined loading [J]. General South Highway Engineering, 2005, 30(3): 53-56.

[4] 赵明华,徐卓君,马缤辉,等.倾斜荷载下基桩C法的幂级数解[J]. 湖南大学学报(自然科学版)，2012,39(3):1-5. ZHAO M H, XU Z J, MA B H,et al.Power series solution for pile based on C-method under inclined loads [J].Journal of Hunan University(Naturnal Science), 2012, 39(3):1-5.

[5] 栾鲁宝,丁选民,周仕礼,等.考虑竖向荷载的桩基水平振动响应的解析解[J].建筑结构, 2015, 45(19):80-86. LUAN L B, DING X M, ZHOU S L,et al. Analytical solution of lateral vibration of a axial loaded pile [J]. Building Structure, 2015, 45(19):80-86.

[7] 王用中,张河水. 弹性地基梁的压弯计算及其应用[J].桥梁建设,1985,14(4):30-52. WANG Y Z, ZHANG H S. Bending calculation of elastic foundation beam and its application [J]. Bridge Construction ,1985,14(4):30～52.(in Chinese)

[8] 赵明华,李微哲,曹文贵. 复杂荷载及边界条件下基桩有限杆单元方法研究[J]. 岩土工程学报,2006,28(9):1059-1064. ZHAO M H, LI W Z, CAO W G. Study on applying finite pole element method to analysis of piles under complex loads with different boundary restraints [J]. Chinese Journal of Geotechnical Engineering, 2006,28(9): 1059-1064.

[9] 夏拥军,陆念力.梁杆结构二阶效应分析的一种新型梁单元[J]. 工程力学,2007,24(7):39-43. XIA Y J, LU N N. A new beam element for second-order effect analysis of beam structures [J]. Engineering Mechanics, 2007,24(7):39-43.

[10] 赵明华,李微哲,单远铭,等.成层地基中倾斜荷载桩改进有限杆单元法研究[J].工程力学，2008,25(5):79-85. ZHAO M H, LI W Z, SHAN Y M, et al. Behavior analysis of piles in layered clays under eccentric and inclined loads by improved finite pole element method[J]. Engineering Mechanics,2008, 28(5): 79-85.

[13] 耿江玮,朱东生,向中富,等.非规则连续梁桥非线性地震反应分析[J].重庆交通大学学报(自然科学版), 2011, 30(2):185-189, 281. GENG J W, ZHU D S, XIANG Z F,et al. Nonlinear seismic response analysis of irregular continuous bridge [J]. Journal of Chongqing Jiaotong University (Natural Science), 2011, 30(2):185-189, 281.

[14] 魏标,崔睿博,戴公连,等.橡胶支座对非规则连续梁桥地震反应的影响[J].中国公路学报, 2013,26(6): 110-117. WEI B, CUI R B, DAI G L, et al. Impact of laminated rubber bearings on seismic response of irregular continuous bridges [J]. China Journal of Highway and Transport, 2013,26(6): 110-117.

[15] 张志俊,李小珍,张迅,等. 弹性支座对桥梁车致振动的隔振效果研究[J].工程力学, 2015, 32(4):103-111. ZHANG Z J, LI X Z, ZHANG X, et al. Study on the vibration-isolation effects of elastic bearings on train-induced vibration of railway bridge [J]. Engineering Mechanics, 2015, 32(4):103-111.

(编辑 胡玲)

LiWeizhe1,2,LouPing2

(1.School of Civil Engineering, Central South University, Changsha 410000,P.R. China；2. China Coal Technology &Engineering Group, Chongqing Design & Research Institute Co. Ltd. Chongqing 400016,P.R. China)

Finite pole element method is presented forP-Δeffect analysis of pile and bearing while shear deformation is well considered. It is assumed that horizontal displacement of the pole element has a longitudinally cubic power function and the shear displacement has a longitudinally linear function, theP-Δeffect pole element rigid equation considering the shear deformation produced by lateral load and the radial component of vertical load, is derived. TheP-Δeffect pole element rigid equation considering the shear deformation only produced by lateral load is derived in the paper. TheP-Δeffect pole element rigid equation considering the shear deformation only produced by the radial component of vertical load, is derived in the paper. And theP-Δeffect pole element considering the shear deformation only produced by lateral load can simulate the bearing working eccentrically well in real-time. Matlab process of finite pole element method forP-Δeffect analysis of pile and bearing is edited, and case analysis is done, and the theory and the method is proved good. Finally conclusions are drawn as follows: (i) theP-Δeffect analysis result of pile will increase obviously while the eccentric bending moment of the bearing is well considered; (ii) the deformation has little effect on theP-Δeffect analysis result of the pile and bearing.

pile; bearing; lateral shear deformation; radial component of vertical load;P-Δeffect; finite pole element method

2016-03-07

李微哲(1981-)，男，主要从事桩基础及路基研究,(E-mail)46414461@qq.com。

10.11835/j.issn.1674-4764.2016.06.009

TU470

A

1674-4764(2016)06-0062-10

Received:2016-03-07

Author brief：Li Weizhe(1981-),main research interests: pile foundation and subgrade engineering, (E-mail)46414461@qq.com.