带有周期势的分数阶Schrödinger-Possion系统基态解的存在性

董晓芳

(山西大学 数学科学学院,山西 太原 030006)



带有周期势的分数阶Schrödinger-Possion系统基态解的存在性

董晓芳

(山西大学 数学科学学院,山西 太原 030006)

研究了R3中一类带有周期势的分数阶Schrödinger-Possion系统基态解的存在性。 在f(x,t)满足一定条件下, 得到能量泛函的山路几何结构,结合变分方法证明了基态解的存在性。

分数阶Schödinger-Possion系统; 周期势; 基态解

0 引言

在本文中, 我们主要讨论如下的带有周期势的分数阶Schrödinger-Possion系统

(1)

的基态解的存在性结果, 其中α∈(0,3),p∈[2,3+α), V是连续的周期势, f是连续的周期函数, φ是第二个方程的弱解。

当α=p=2时, 系统(1)表示如下的Schrödinger-Possion系统

(2)

当N≥3,α∈(0,N),p∈[2,(N+α)/(N-2))及非线项f=0,系统(1)可化为如下的方程

(3)

系统(2)在物理学中的应用非常广泛, 它是在描述非线性Schrödinger方程与静电场相互作用的孤立波的量子力学模型中提出的, 参看文献([1,2])。

近年来, 与方程(3)相似的Choquard方程

(4)

的解的存在性和解的相关性质已经被广泛的研究。 在文献[3]中, Lions第一次通过临界点理论研究了Choquard方程非平凡解的存在性; 在文献[4]中, 作者考虑了p≥2时广义的Choquard方程, 当N,α,p定义在某个非空实数集上, 他们证明了方程的每个正解是径向对称的并且关于某个点是单调递减的; 在文献[5]中, 与[4]相同的假设下, 作者研究了在电磁势情形下解的存在性和多重性结果并且建立了基态解在无穷远处的渐近衰减性; 在文献[6]中, 作者消除了[5]中的限制条件并且证明了当参数在一个合适的范围时基态解的正则性, 径向对称性以及无穷远处的渐近衰减性; 在文献[7]中, 作者研究了线性势函数和非线性势函数对广义Choquard 方程基态解的存在性与集中性的作用。

(V) V是连续的, 关于xi是1-周期的且V0=infx∈R3V(x)>0, 其中i=1,2,3。

本文研究的主要结果是:

定理1 假设(V)和(f1)-(f4)成立, 则系统(1)存在一个基态解。

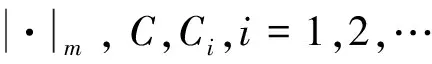
1 准备工作

首先,我们给出Sobolev空间E:=H1(R3)。 在条件(V)的假设下, 定义E中的一个新范数

它与E中的标准范数是等价的。

命题1[8](Hardy-Littlewood-Sobolev 不等式)设s,r>1,μ∈(0,N)满足1/s+μ/N+1/r=2, 则存在一个正常数C(s,N,μ,r)使得对所有的f∈Ls(RN)和h∈Lr(RN),

注记1 取μ=3-α,s=r=6/(3+α)。由命题1和逆Hölder不等式([9, p.25])有

Iα*w∈L6/(3-α)(R3), w∈L6/(3+α)(R3)

(5)

进一步, 它是由L6/(3+α)(R3)到L6/(3-α)(R3)的有界线性算子, 其中Iα:R3→R是Riesz势, 定义如下([10]):

为了方便, 我们作如下记号:

从而系统(1)可化成一个带有非局部项的椭圆方程,

现在我们定义系统(1)相应的I:E→R

根据f的假设条件和注记2, 我们知道I的定义是合理的且I∈C1(E,R),

〈I'(u),v〉=∫[▽u·▽v+Vuv]+

易知, 系统(1)的基态解是泛函I的解w∈E且满足

I(w) = infv∈NI(v)

其中N是系统(1)相应的Nehari流行, 定义如下:

N={v∈E{0}:〈I′(v),v〉=0}

2 主要结果

引理1 对每一个u∈E,

(i) 对任意的t>0, φtu=tpφu;

(ii) 在E中, 若un⇀u且un→u a.e x∈R3, 则在L6/(3-α)(R3)中, φun⇀φu。

证明 (i) 直接计算可得结论。

(ii) 令r=6/(3+α)。 为了证明结论, 只需证明对任意的φ∈Lr(R3), 我们有

〈φun,φ〉→〈φu,φ〉

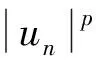
因此,

引理2 假设(V)和(f1)-(f4)成立, 则有下列结论:

(i)对于给定的u∈E{0}, 存在唯一的tu=t(u)>0使得m(u): = tuu∈N且I(m(u))=maxt≥0I(tu);

(ii) 对所有的u∈N,存在β>0使得‖u‖≥β;

(iii)I在N上有正下界且是强制的使得u∈N, ‖u‖→ + ∞, I(u)→ + ∞;

(iv)假设ν∈E{0}是一个紧子集, 则存在R>0使得在R+νBR(0)有I≤0。

证明 由条件(f1), (f2)及(f4)可知, 对任意的ε>0, 存在Cε>0使得

(6)

F(x,t)≥0, f(x,t)t≥2pF(x,t)≥0

(7)

(i)对于t>0, 我们设

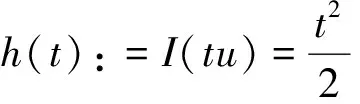
一方面, 由(6), E连续嵌入Lp(R3)及E连续嵌入Lq(R3), 则对ε充分小, 我们有

由于u≠0, p≥2及q>4, 故当t>0充分小, 我们有h(t)>0。

另一方面, 由命题1可知

(8)

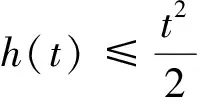
因此, maxt≥0h(t)在tu=t(u)>0是可达的且使得h′(tu)=0,tuu∈N。

结合

有

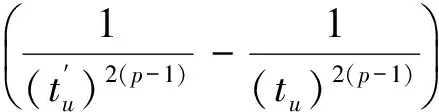
显然, 与条件(f4)矛盾。

(ii) 由u∈N和(6),则对ε充分小, 我们有

因为p∈[2,3+α)和q∈(4,6), 故对所有的u∈N, 存在β>0使得‖u‖≥β。

(iii) 对所有的u∈N, 由(7)和(ii)可得

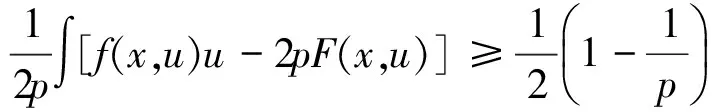
故I在N上是有正下界的。 显然也是强制的。

从而

结合(8)，我们有

显然矛盾, 故结论成立。

下面的两个引理来自文献[11]。

引理3 设E中的单位球S:={u∈E:‖u‖=1}, 则映射S→N,u|→m(u)是连续的。

证明 令u0∈S。为了证明结论, 只需证明序列(un)⊂S,un→u0, 则m(un)→m(u)。事实上, 由引理2 (i), 我们可设m(un):=tunun,m(u0):=tu0u0。若(un)⊂S,un→u0。由引理2 (i)和(iv)知, 存在R>0使得

故由引理2(iii)知序列(m(un))有界。 从而存在一个子列, 不失一般性设为

tun:=‖tunun‖→t≠0

事实上, 由于tunun∈N和引理2 (ii), 我们有β≤‖tunun‖=tun→t。 再由于N是闭的线性子空间, 所有根据引理2 (i)可得

m(un)=tunun→tu0=tu0u0=m(u0)

进一步, 根据引理2, 我们有重要的发现: m是S到N的同胚映射且其逆映射为

(9)

现在我们考虑泛函Φ:S→R定义如下:

Φ(w)=I(m(w))

引理4 (i)Φ∈C1(S,R), 且Φ'(w)z=‖m(w)‖〈I′(m(w)),z〉对任意的 z∈TwS={v∈E:〈v,w〉=0}。

(ii) (wn)是Φ的一个Palais-Smale序列当且仅当(m(wn))是I的一个Palais-Smale序列。

(iii) w∈S是Φ的一个临界点当且仅当m(w)∈N是I的一个临界点。 进一步, Φ和I相应的临界值是相同的且infsΦ=infNI

为了证明定理1的存在性, 我们有必要研究在N上I的极小化序列的一些性质。

引理5[12]令r′>0。 如果(un)在H1(R3)中有界且

则在Ls(R3)中, un→0, 其中s∈(2,6)。

引理6 若(un)⊂N是I的一个极小化序列, 则

(i) (un)在E中有界;

(ii) 经过适当的Z3-平移, 在子列的意义下, 存在u∈E使得un⇀u≠0且I(u)=infNI

证明 (i) 由引理2(iii)易知, (un)在E中有界。

(ii) 令c=infNI由(i)知存在序列(un)的子列不妨仍记为(un)使得, 在E中, un⇀u。 假设

(10)

则由引理5可知在Ls(R3)中, un→0, 其中s∈(2,6)。 再由(6)和(un)的有界性可知

因此,

这意味着‖un‖→0, 与引理2(ii)矛盾。 故(10)不成立。从而存在r′,δ>0及序列(yn)⊂R3使得

因此, 在子列的意义下,un⇀u≠0。 进一步,I′(u)=0。

〈I′(u),w〉=0

由Vitali定理[13,p.133], 我们有

(11)

另一方面, 由引理1 (ii) 知, 在L6/(3-α)(R3)中,φun⇀φu。 再由Hölder不等式可得

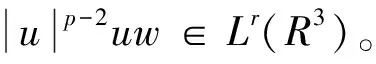
(12)

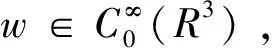
其中θ∈(0,1),pr∈(2,6)。 由注记1可知φun在L6/(3-α)(R3)中有界, 故由Hölder不等式有

进而

(13)

由(12)和(13)知

(14)

由于在E中un⇀u, (11)及(14)可得

从而u∈N。 显然I(u)≥c。 为了完成证明, 只需证明I(u)≤c。 事实上, 根据(7), 范数的弱下半连续, Fatou引理及(un)的有界性, 我们有

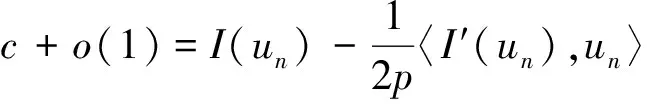
这意味着I(u)≤c。

定理1的证明 令c=infNI。 由引理2 (iii)知c>0。 进一步, 如果u0∈N满足I(u0)=c, 则m-1(u0)∈S是Φ的一个极小值且是Φ的一个临界点。 事实上, 由引理3和(9)可知, 存在w0∈S使得w0=m-1(u0)=u0/‖u0‖。 从而由引理4 (i)可得

再根据[12, p.87, Proposition 5.12], 存在λ∈R使得Φ′(w0)=λw0, 则0=[Φ′(w0),w0]=λ‖w0‖2=λ。 因此, Φ′(w0)=0。 再由引理4 (iii)知, u0是I的一个临界点。

下面证明存在一个I|N上的最小值。 事实上, 根据Ekeland变分原理[12, p.9], 存在一个序列(wn)⊂S使得当n→∞满足Φ(un)→c,Φ′(un)→0。令un=m(wn)。由引理4 (ii)可得当n→∞满足I(un)→c,I′(un)→0。 因此, (un)是I在N上的极小化序列。 从而由引理6可知, 存在I|N上的极小值。

[1] BENCI V,FORTUNATO D.An eigenvalue problem for the Schrödinger-Maxwell equations[J].Topol Methods Nolinear Anal,1998,11(2):283-293.

[2] 郝悦斌,李鸿翔.全空间中椭圆方程组解的存在性[J].贵州师范大学学报(自然科学版),2016,34(1):44-48.

[3] LIONS P L.The Choquard equation and related questions[J].Nolinear Anal,1980,4(6):1063-1072.

[4] MA L,ZHAO L.Classification of positive solitary solutions of the nonlinear Choquard equation[J].Arch Ration Mech Anal,2010,195(2):455-467.

[5] CINGOLANI S,CLAPP M,SECCHI S.Multiple solutions to a magnetic nonlinear Choquard equation[J].Z Angew Math Phys,2012,63(2):233-248.

[6] MOROZ V,SCHAFTINGEN J V.Groundstates of nonlinear Choquard equations:existence,qualitative properties and decay asymptotics[J].J Funct Anal,2013,265(2):153-184.

[7] ALVES C O,YANG M B.Existence of semiclassical ground state solutions for a generalized Choquard equation[J].J Differential Equations,2014,257(11):4133-4164.

[8] LIEB E H,LOSS M.Analysis[M].Second edition. Providence,RI:American Mathematical Society,2001:1-346.

[9] ADAMS R A,FOURNIER J J F.Sobolev spaces[M].Second edition.Amsterdam:Elsevier/Academic Press,2003:1-305.

[10]RIESZ M.L'intégrale de Riemann-Liouville et le problème de Cauchy[J].Acta Math,1949,81:1-223.

[11]SZULKIN A,WETH T.Ground state solutions for some indefinite variational problems[J].J Funct Anal,2009,257(12):3802-3822.

[12]WILLEM M.Minimax theorems[M].Boston:Birkhäuser,1996:1-162.

[13]RUDIN W.Real and complex analysis[M].New York:London ect:McGraw-Hill,1966:1-412.

Existence of ground state solution for fractional Schrödinger-Possion system with periodic potential

DONG Xiaofang

(School of Mathematical Science, Shanxi University, Taiyuan,Shanxi 030006, China)

In this paper，we study the existence of ground state solution for a class fractional Schrödinger-Possion system with periodic potential in R3.Under the suitable assumptions of f(x,t)，the mountain pass geometric of energy functional is obtained.We can prove ground state solution of the system by variational methods.

fractional Schrödinger-Possion system； periodic potential； ground state solution

1004—5570(2016)06-0059-06

2016-08-12

国家自然科学基金(11301313, 11101250), 山西省自然科学基金(2012011004-2, 2013021001-4)

董晓芳(1990-),女,硕士,研究方向:非线性泛函析,E-mail:1032152055@qq.com.

O175.25;O177

A