一个改进的基于身份具有消息恢复功能代理签名方案

金婷婷，邓伦治*，蒋昊天

(1.贵州师范大学 数学科学学院，贵州 贵阳 550001；2.北京航空航天大学自动化科学与电气工程学院，北京 100083)



一个改进的基于身份具有消息恢复功能代理签名方案

金婷婷1，邓伦治1*，蒋昊天2

(1.贵州师范大学 数学科学学院，贵州 贵阳 550001；2.北京航空航天大学自动化科学与电气工程学院，北京 100083)

在具有消息恢复功能签名方案中，原始信息被包含在签名中，其不需要发送给验证者，因此降低了签名的长度。Singh和Verma提出了一个具有消息恢复功能的基于身份的代理签名方案，Niu等人指出了其方案是不安全的，然后给出了一个改进方案，并宣称改进方案是安全的。然而通过对Niu等人给出方案的分析，发现其方案依然是不安全的，当攻击者获得一个有效签名时，他可以对任何一个消息进行伪造签名。为了解决该方案的安全缺陷，对其方案进行了改进，改进的方案可以有效抵抗伪造攻击。与之前的方案相比，效率更高。

基于身份密码；代理签名；消息恢复；伪造攻击；安全性

0 引言

在传统公钥密码体制中，有一个可信的证书颁布机构(CA)，其负责向用户颁发证书，绑定用户的公钥与私钥，因此带来了证书管理的问题。1984年，Shamir[1]提出了基于身份的密码体制，有一个可信的私钥产生中心(PKG)，将用户的身份信息(身份证号码，邮箱地址等)作为用户的公钥，PKG利用系统公钥，根据用户身份信息生成用户私钥，并将其发送给用户，从而解决了证书管理的问题。1996年，Mambo[2，3]首次提出代理签名的概念，它是一种用来解决数字签名权力的代理问题的特殊的数字签名，在该方案中，验证者需要同时验证签名和原始签名人的代理协议。在具有消息恢复功能签名中，原始信息被附加到签名中，无需和签名一起发送给代理签名者，任何人无需任何秘密信息的情况下都可恢复含于签名中的消息，其最大限度地减少了签名的总长度，特别适合在宽带受限的网络环境中使用。

利用双线性对技术，文献[4]提出了第一个基于身份的代理签名方案。在代理签名方案的基础上，文献[5]提出了一个带消息恢复功能的基于身份的数字签名方案。文献[6、7]对该签名方案进行了改进，分别给出了一个效率更高的方案。文献[8、9]分别给出了一个具有更高安全性要求的基于身份的代理签名方案。文献[10]使用自认证公钥提出了一个带消息恢复功能的代理签名方案。文献[11]给出了一个基于身份的具有部分消息恢复功能的签名方案，在标准模型下，该方案对自适应选择消息攻击是存在不可伪造的。文献[12]提出了一个带消息恢复功能的基于身份的代理签名方案，该方案的安全性规约为CDH问题。最近，文献[13]对文献[12]中方案进行了分析，给出了一个改进的方案。通过仔细的研究，发现文献[13]中的改进方案也不满足不可伪造性，当攻击者获得一个有效的代理签名时，他可以使任何消息的签名成为有效签名。本文对其方案的不足进行了改进。

1 预备知识

1.1 双线性映射

设G1是一个素数q阶加法循环群，P是G1的一个生成元，G2是一个素数q阶乘法循环群。一个双线性对是一个映射e:G1×G1→G2，满足双线性、非退化性和可计算性。

2)非退化性：存在P，Q∈G1，满足e(P，Q)≠1。

3)可计算性：对于任意的P，Q∈G1，存在有效的多项式时间算法，可以计算出e(P，Q)。

1.2 困难问题假设

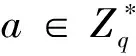
2)计算Diffie-Hellman(CDH)问题：设G1是一个q阶加法循环群，P是G1的一个生成元，已知aP，bP，是否能计算出abP。

3)判定Diffie-Hellman问题：设G1是一个q阶加法循环群，P是G1的一个生成元，已知aP，bP，cP，问等式cP=abP是否成立。

4)计算双线性Diffie-Hellman问题：设G1是一个q阶加法循环群，P是G1的一个生成元，已知aP，bP和cP，是否能计算出e(P，P)abc。

1.3 符号约定

1)a‖b：两个字符串a和b的串联；

2)⊕：在二进制系统中的XO-R计算；

3)[x]10：把x∈{0，1}*用十进制表示；

4)[y]2：把y∈Z用二进制表示；

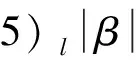
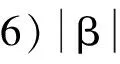
2 Niu等方案的回顾

本文回顾了Niu等的方案，该方案由以下7个步骤组成，并且涉及到3个主要实体：原始签名者A、代理签名者B和验证者C。

2)私钥生成：输入用户U的身份IDU∈{0，1}*，PKG计算U的私钥dU=sH0(IDU)和公钥qU=H0(IDU)，并通过安全信道把(qU,dU)发送给U。

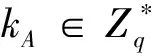
4)代理授权验证：当B收到WA→B=(mw,rA,S)后，先计算hA=H1(mw,rA)，qA=H0(IDA)，然后验证等式e(S,P)=e(qA,Ppub)hA·rA是否成立，如果成立，则接受WA→B；否则，认定WA→B是无效的。

5)代理密钥生成：B接受WA→B=(mw,rA,S)后，计算代理签名密钥dP=hA·dB+S，这里hA=H1(mw,rA)。

rB=e(p,p)kB，

hB=H1(m,rB)，

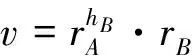
β=F1(m)‖(F2(F1(m))⊕m)，

α=[β]10，

VB=H2(v)+α，

U=kBP+hBdP。

然后通过安全信道把δ=(rA,hB,VB,mw,U)发送给C。

7)代理签名验证/消息恢复：C接收到代理签名δ=(rA,hB,VB,mw,U)后，首先检查A与B的信息与mw所含信息是否一致。若符合则进行以下计算：

hA=H1(mw,rA)，

α=VB-H2(e(U,P)·e(qA+qB,Ppub)-hAhB)，

β=[α]2

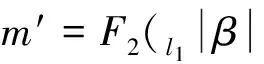
3 Niu等方案的分析

通过观察代理签名中的式子VB=H2(v)+α与代理签名验证算法中的式子α=VB-H2(e(U,P)·e(qA+qB,Ppub)-hA hB)，看等式v=e(U，P)·(qA+qB,Ppub)-hAhB是否成立。

验证如下：

e(U，P)·e(qA+qB，Ppub)-hAhB

=e(kBP+hBdp，P)·e(qA+qB，Ppub)-hAhB

=e(kBP，P)·e(hBdp，P)·

e(qA+qB，Ppub)-hAhB

=e(P，P)kB·e(dp，P)hB·e(qA+qB，Ppub)-hAhB

=rB·e(hAdB+hAdA+kAP，P)hB·e(qA+qB，Ppub)-hAhB

=rB·e(hAdB+hAdA)hB·e(kAP，P)hB·

e(qA+qB，Ppub)-hAhB

=rB·e(qA+qB，Ppub)hAhB·e(kAP，P)hB·

e(qA+qB，Ppub)-hAhB

=v

α=VB-H2(v)，

β=[α]2=F1(m)‖(F2(F1(m))⊕m)。

因此，若攻击者能够得到一个有效的签名δ=(rA,hB,VB,mw,U)，他能从等式e(U，P)·(qA+qB,Ppub)-hAhB=v中计算出v，这里hA=H1(mw,rA)，但是在验证阶段对hB并没有进行任何的检验， 并不能体现hB的值是随着rB的值一起改变的，换句话说，对不同的消息m，选取相同hB进行签名，都是可以通过验证算法的。因此，对任意的消息m*∈{0，1}l2，攻击者可以进行如下计算：

β*=F1(m*)‖(F2(F1(m*))⊕m*) ，

α*=[β*]10，

当验证者收到签名δ*后，计算：

hA=H1(mw，rA)，

β*=[α*]2，

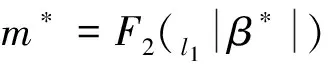
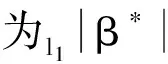
4 改进的方案

在Niu等的方案中，当攻击者获得一个有效的代理签名δ后，他可以通过验证等式v=e(U,P)·e(qA+qB,Ppub)-hAhB计算出v，所以攻击者在不知道代理私钥的前提下，可以对任意的消息进行签名，且为有效签名。为了阻止这种攻击，下面对代理签名、代理签名验证/消息恢复进行了改进。

rB=e(P,P)kB，

hB=H1(m,rB)，

v = rAhB·rB，

β=F1(m)‖(F2(F1(m))⊕m)，

α=[β]10，

VB=H2(v)+α，

U=hAP+hBdP。

2)代理签名验证/消息恢复：当C收到δ后，先检查A与B的信息与是否一致，若一致，继续以下计算：

hA=H1(mw,rA)，

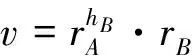
检验v=e(U,P)·e(qA+qB,Ppub)-hAhB是否成立，若成立，则进行以下计算：

α=VB-H2(v)，

β=[α]2，

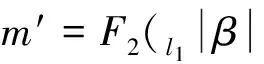
改进方案的验证等式与Niu的方案相同，

α=VB-H2(v)，

β=[α]2=F1(m)‖(F2(F1(m))⊕m)，

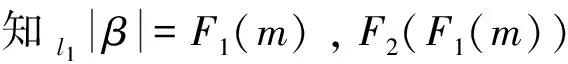
5 安全性和效率分析

5.1 安全性分析

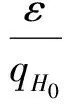
为了证明以上定理，首先定义一个的具有消息恢复功能的通用数字签名方案。

参数设置：给定λ作为安全参数，生成密钥对的过程如下：

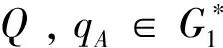
2)随机选取mw∈{0,1}*，对委托消息mw使用密钥dA，应用文献[6]的方法计算签名(mw,rA,UA)。

3)计算hA=H1(mw,rA)和dp=hA·d+UA。

4)公开参数为(G1,G2,H0,H1,F1,F2,e,q,p,Q,qA,mw,,hA,rA)，私钥为dp。

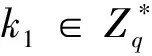
签名验证：接受者收到签名δ=(rA,rp,hB,VB,mw,U)后，计算

hA=H1(mw,rA)，

α=VB-H2(e(U,P)·e(qA+Q,Ppub)-hAhB)，

β=[α]2。

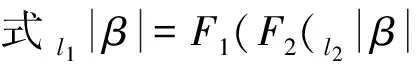
定理的证明 通常假定攻击者A在进行私钥生成，代理授权，代理密钥生成，代理签名算法之前，可以对任何的身份ID向H0进行多次密钥询问。

1)挑战者B运行系统参数算法，生成一组参数

params=(G1,G2,H0,H1,H2,F1,F2,e,Ppub,q,Q,qA,mw,rA,λ,l1,l2,hA)。

2)令Ppub←aP，i←1。

3)令Clist，Dlist，Glist，Slist初始为空集。

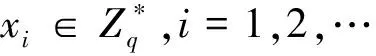
qH0。

5)B把公开参数params发送给A，并让A模拟本中改进的签名方案，在密钥生成阶段，B通过以下方法推到A要获取的预言信息。

H0查询：输入指定身份ID，B检查H0(ID)是否被定义，若未定义，则

并且让IDi←ID，i←i+1，并把H0(ID)返回给攻击者A。

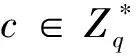
私钥查询：攻击者A向B输入IDi，如果i=t，则终止算法，否则计算di=xiPpub响应A，并将(IDi,di)加入集合Clist。

代理授权查询：输入IDi和委托信息mw，如果i≠t，B计算di=xiPpub作为其密钥对mw使用文献[6]提出的签名方案进行签名并获得(r0,s0)，否则，按如下的步骤推到的代理委托权。

2)计算r0=e(S0,P)·e(Q,Ppub)-h0；

3)如果攻击者A向H1做过(mw,r0)查询，则算法终止(出现碰撞)，否则设置H1(mw,r0)=h0，并计算W=(mw,r0,S0)来响应攻击者，同时把(IDi,mw,W)加入集合Dlist。

代理私钥查询：输入代理签名者IDj的身份和委托书W=(mw,r0,S0)，如果j=t，则终止算法，否则B计算dp=H1(mw,r0)xjPpub+S0来响应攻击者A，并把(W,IDj,dp)加入集合Glist。

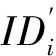
2)检查H1(mw,r0)是否被定义，若未定义，通过(mw,r0)询问随机预言机H1并返回h=H1(mw,r0)；

3)计算rp= e(U',P)·(e(xiP, + Q)hhp·r0hp)-1，Up=U′；

4)如果攻击者A向H2进行过(rp,r0)询问，则终止算法(出现碰撞)，否则计算Vp= H2(r0hp·rp) + [β]10，其中β=F1(m)‖(F2(F1(m))⊕m)；

5)输出δ=(r0,rp,hp,Vp,mw,Up)，并把(W,m,δ)加入到集合Slist中。

伪造：如果攻击者A用指定的身份信息和代理签名者身份信息获取了签名(W,m,δ)=((mw,r0,S0),m,(r0,rp,hp,Up,mw,Vp))，并满足PVerify((m,δ),IDi)=1，(W,m,δ)，∉Slist，(IDj,dj)∉Clist，(IDj,W,dp)∉Glist，j=t，则B成功伪造了签名δ=(r0,rp,hp,Vp,mw,Up)和应用的代理私钥dp=aQ，其中h=H1(mw,r0)。

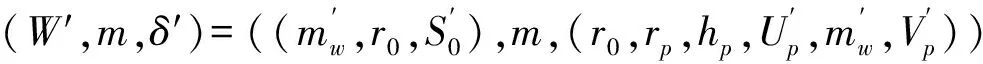
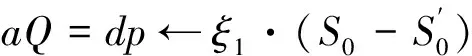
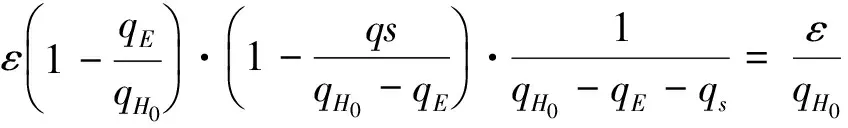
所以，在随机预言模型下，在自适应选择身份和消息攻击条件下，本文改进的方案是不可伪造和可委托的，其安全性规约为CDH问题。

5.2 效率分析

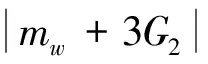
6 结束语

在一些需要低消耗的环境，特别是宽带受限的网络中，需要长度更短一些的签名，因此具有消息恢复功能的签名具有更强的适应性。通过对Niu等人方案的分析，发现其方案是不安全的，因此，本文给出了完整的攻击算法和改进方案。

[1] SHAMIR A.Identity-based cryptosystems and signature scheme[C].Advances in Cryptology’196,LNCS 196.Berlin:Springer,1984:47-53.

[2] MAMBO M,USUDA K,OKAMOTO E.Proxy signatures: Delegation of the power to sign message[J].IEICE Transactions Fundamentals of Electronic Communications and Computer Science,1996,E97-A(9):1338-1354.

[3] MAMBO M,USUDA K,OKAMOTO E. Proxy signing operation [C].Proceedings of the 3rdACM Conferenceon Computer and Communication Security(CCS)，New York ：ACM Press,1996:48-57.

[4] ZHANG F,KIM K.Efficient ID-based blind signature and proxy signature from bilinear pairings[C].ACISP’2003，LNCS 2727.Berlin:Springer-Verlag，2003:312-323.

[5] ZHANG F，SUSILO W，MU Y.Identity based partial message recovery signature(or how to shorten ID-based signature)[C]//FC’2005,LNCS-3570.Berlin:Springer,2005:45-56.

[6] GU C，ZHU Y.Probable secuirty of ID-based proxy signature schemes[C].ICCNMC’2005,LNCS 3619.Berlin:Springer-Verlag,2005:1277- 1286.

[7] TSO R，GU C，OKAMOTO E.An efficient ID-based digital signature scheme with message Recovery[C].Cryptology and Network Security,LNCS 4856.Berlin:Springer,2007:47-59.

[8] WU W，MU Y，SUSILO W,et al. Identity based proxy signature from pairing[C].The 4thInternational Conference on Autonomic and Trusted Computing,LNCS 4610.Berlin:Springer-Verlag,2007:22-31.

[9] WANG B.A new identity based proxy signature scheme [EB/OL].Cryptology Eprint Archive Report，2008.http://www.Eprint.iacr.org/2008/323.

[10]WU T，HSU C，LIN H.Self certified multi proxy signature sche-me with message recovery[J].Zhejiang Univ Sci,2009,10(2):290-300.

[11]刘振华，张襄松，田绪安，等.标准模型下基于身份的具有部分消息恢复功 能的签名方案[J].北京工业大学学报，2010,36(5):654-658.

[12]SINGH H，VERMA G K.ID-based proxy signature scheme with message recovery[J].The Journal of Systems and Software，2012，85:209-214.

[13]牛永正，亢保元，许昊.改进的基于身份的代理签名方案[J].计算机应用，2015，35(SI):63-65.

An improved ID-based proxy signature scheme with message recovery

JIN Tingting1,DENG Lunzhi1*,JIANG Haotian2

(1.School of Mathematical Science, Guizhou Normal University, Guiyang, Guizhou 550001,China;2.School of Automations Science and Electrical Engineering, Beihang University,Beijing,100083,China)

A digital signature scheme with message recovery is a signature scheme in which the original message of the signature is not required to be transmitted together with the signature, so it can reduce the length of the signature. Singh and Verma proposes a new ID-based proxy signature scheme with message recovery. Niu et al. pointed out the scheme was unsafe, and proposed an improved scheme, and announced the improved scheme is safe. The scheme was found insecure through the analysis, the attacker can give a forgery signature when he gets a valid signature. In order to overcome the weakness of the scheme, an improved scheme was proposed, which can resist the forgery attack. Compared with the previous schemes, the improved scheme is more efficient.

ID-based cryptography; proxy signature; message recovery; forgery attack; security

1004—5570(2016)06-0098-06

2016-06-28

国家自然科学基金项目(61562012)；贵州省教育厅创新群体重大研究项目(黔教合KY字2016[026])

金婷婷(1990-)，女，硕士研究生，研究方向：密码学,E-mail：804083709@qq.com.

*通讯作者：邓伦治(1979-)，男，教授，博士，研究方向：密码与信息安全，E-mail：381651551@qq.com.

TP391

A