一类多圈图关于Merrifield-Simmons指标的计数

刘睿琳，田双亮，田文文

(西北民族大学 数学与计算机科学学院，甘肃 兰州 730030)



一类多圈图关于Merrifield-Simmons指标的计数

刘睿琳，田双亮，田文文

(西北民族大学 数学与计算机科学学院，甘肃 兰州 730030)

图G的Merrifield-Simmons指标表示该图中所有独立集的数目。主要研究了一类多圈图Gm(n)关于Merrifield-Simmons指标的计数问题，并给出了具体的表达式。

多圈图；Merrifield-Simmons指标；计数

0 引言

自1989年美国化学家Merrifield和Simmons在文献[1]中提出Merrifield-Simmons指标之后，由于这一化学拓扑指标与物质的沸点有着密切的关系，且有着相当广泛的应用，参见文献[2,3]。随后，国内外很多学者对此进行了大量的研究工作，文献[4]中关于最大和最小的Merrifield-Simmons指标和Hosoya指标给出了一个很好的综述，并提出了一些有待解决的公开问题。文献[5]中研究了两类多元素链在不同构联接位下的Merrifield-Simmons指标的计数问题。文献[6]中研究了一类(n，n+2)-图关于两种拓扑指标的排序。本文研究了一类多圈图Gm(n)关于Merrifield-Simmons指标的计数问题，并给出了具体的表达式。文中未加说明的符号及术语参见文献[7]。

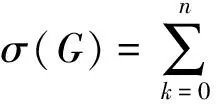
本文研究的多圈图Gm(n)是由n个m阶圈Cm(1),Cm(2),…,Cm(n)构成的圈序列，其中满足相邻两个圈之间只有一个公共顶点。

不妨设V(Cm(i))∩V(Cm(i+1))={ui},i=1,2,…,n，Cm(n+1)=Cm(1)，且d(ui,ui+1)=k，如图1所示。

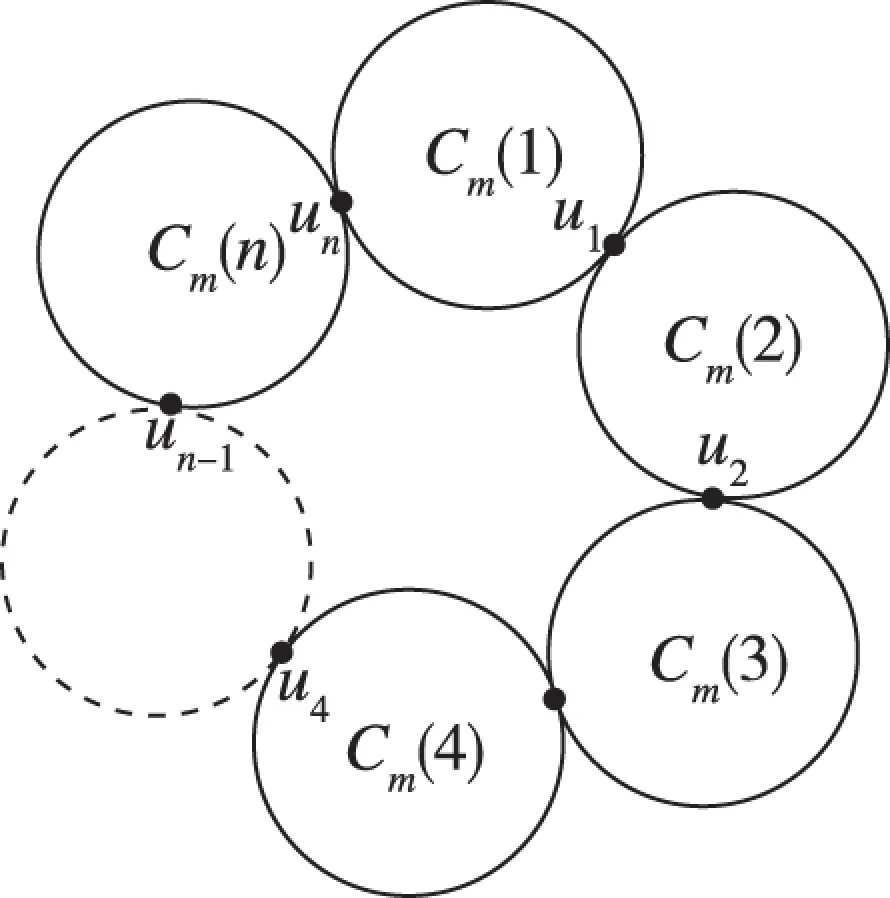
图1 多圈图Gm(n)Fig.1 some-cycle graphGm(n)

在证明主要结论之前，先给出几个相关引理如下。

引理1[2]设G是一个简单的连通图，对任意的u，v∈V(G)，uv∈E(G)，则有(i)σ(G)=σ(G-v)+σ(G-NG[v])；(ii)σ(G)=σ(G-uv)-σ(G-(NG[u]∪NG[v]))。

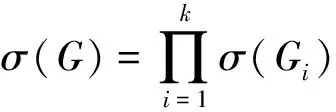
引理3[2]对于n阶的路Pn，有σ(Pn)=fn+2。

1 主要结论及其证明

引理4 对于如图2所示的图H，其Merrifield-Simmons指标为：

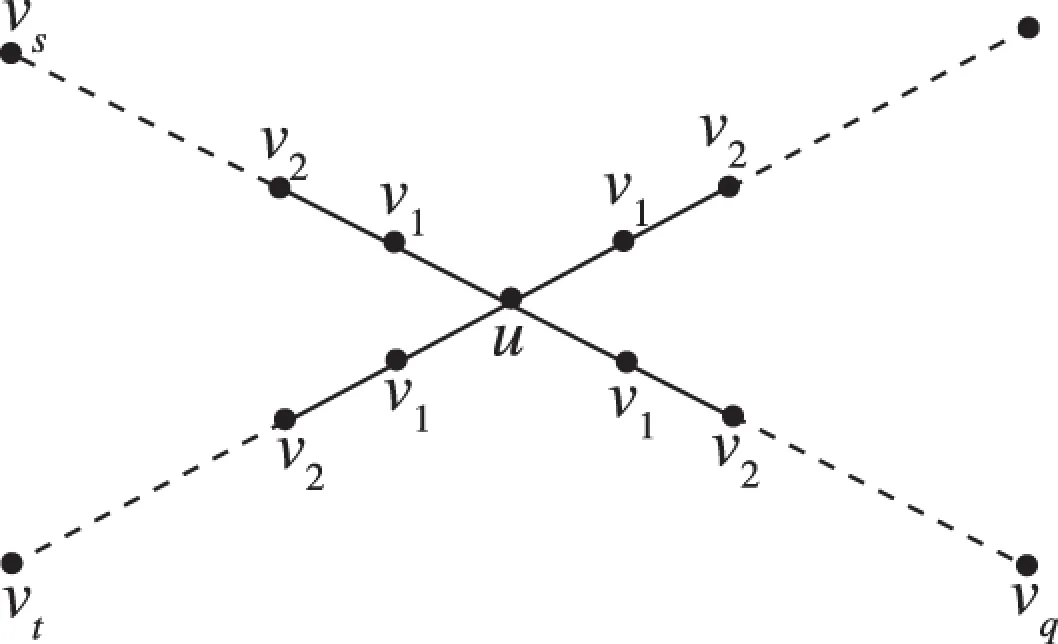
图2 图HFig.2 graphH

证 由引理1-3可得

σ(H)=σ(H-u)+σ(H-NH[u])

=fs+2ft+2fp+2fq+2+fs+1ft+1fp+1fq+1

从而引理4得证。

引理5 对于如图3所示的图Hm(1)，其Merrifield-Simmons指标为：

σ(Hm(1))=(fs+2ft+2fs+1ft+1)

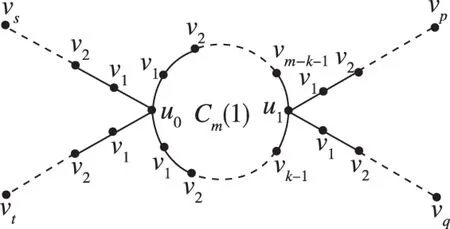
图3 图Hm(1)Fig.3 graphHm(1)

证 由引理1-4可得

σ(Hm(1))=σ(Hm(1)-u1)+σ(Hm(1)-NHm(1)[u1])

=fp+2fq+2·(fs+2ft+2fm-k+1fk+1+fs+1ft+1fm-kfk)+

fp+1fq+1·(fs+2ft+2fm-kfk+fs+1ft+1fm-k-1fk-1)

从而引理5得证。

定理1 对于如图4所示的图Hm(n)，其Merrifield-Simmons指标为：

σ(Hm(n))=(fs+2ft+2fs+1ft+1)

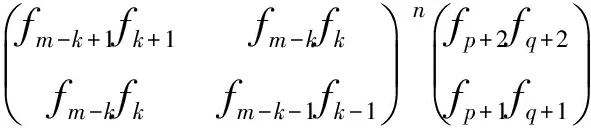
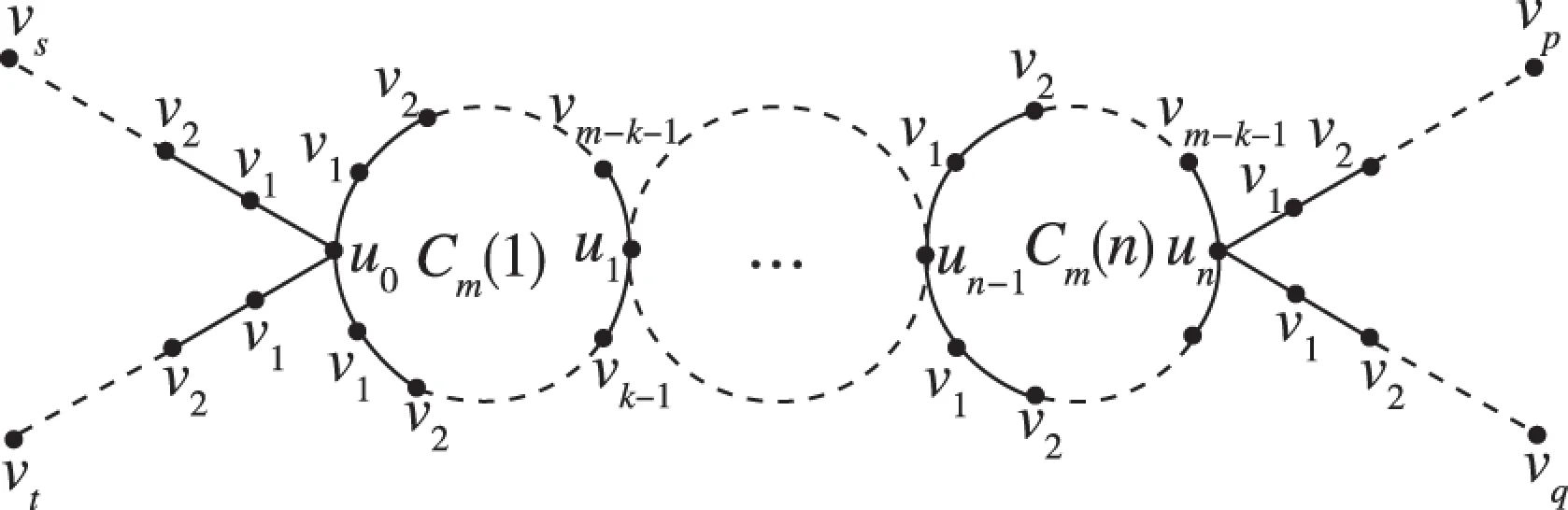
图4 图Hm(n)Fig.4 graphHm(n)

证 由数学归纳法可知

当n=1时，由引理5可知结论成立。

假设当n=r时结论成立，即

σ(Hm(r))=(fs+2ft+2fs+1ft+1)

则当n=r+1时，有

σ(Hm(r+1))=σ(Hm(r+1)-ur+1)+σ(Hm(r+1)-NHm(r+1)[ur+1])

=fp+2fq+2·(fs+2ft+2fs+1ft+1)

fp+1fq+1·(fs+2ft+2fs+1ft+1)

令p=m-k-1，q=k-1，则有

σ(Hm(r+1))=(fs+2ft+2fs+1ft+1)

即当n=r+1时，结论亦成立。

故σ(Hm(n))=(fs+2ft+2fs+1ft+1)

定理2 对于多圈图Gm(n)，其Merrifield-Simmons指标为：

σ(Gm(n))=(fm-k+1fk+1fm-kfk)

证 由引理1及定理1可知

σ(Gm(n))=σ(Gm(n)-un)+σ(Gm(n)-NGm(n)[un])

从而定理2得证。

[1]MERRIFIELDRE，SIMMONSHE．TopologicalMethodsinChemistry[M]．NewYork：Wiley，1989．

[2]GUTMANI，POLANSKYOE．MathematicalConceptsinOrganicChemistry[M]．Berlin：Sprin-ger，1986．

[3]GUTMANI，CYVINSJ．IntroductiontotheTheoryofBenzenoidHydrocarbons[M]．Berlin：Springer，1989．

[4]WAGNERS，GUTMANI．MaximaandminimaoftheHosoyaIndexandtheMerrifield-Simmonsindex[J]．ActaApplMath,2010，112：323-346．

[5] 田双亮，田文文，王倩，等．多元素链的Merrifield-Simmons指标和Hosoya指标[J]．山西大学学报(自然科学版)，2014，37(1)：48-52．

[6] 田文文，田双亮，王燕凤．一类(n,n+2)-图关于两种拓扑指标的排序[J]．贵州师范大学学报(自然科学版)，2015，33(6)：53-56．

[7]BONDYJA，MURTYUSR．Graphtheorywithapplications[M]．NewYork：Macmillan，1976．

The number of a class of some-cycle graph with respect to Merrifield-Simmons index

LIU Ruilin，TIAN Shuangliang，TIAN Wenwen

(School of Mathematics and Computer Science，Northwest University for Nationalities，Lanzhou，Gansu 730030，China)

The Merrifield-Simmons index of a graph is defined as the total number of its independent sets．In this paper，We mainly discuss the number of a class of some-cycle graph Gm(n) with respect to Merrifield-Simmons index，and the specific expression is given．

some-cycle graph；Merrifield-Simmons index；counting

1004—5570(2016)06-0074-03

2016-09-19

国家民委科研项目(14XBZ018)；甘肃省自然科学基金(145RJZA158)；西北民族大学中央高校基本科研业务费专项资金资助研究生项目(Yxm2015180，Yxm2015182)；西北民族大学中央高校基本科研业务费专项资金项目(31920160064)

刘睿琳 (1993- )，女，甘肃永靖人，硕士生，研究方向：组合数学与图论，E-mail: liuruilin0928@163.com．

O157.5

A