基于有限元原理对建筑基坑边坡支护稳定性的计算研究

刘占宏

(陕西国防工业职业技术学院 建筑与热能分院,陕西 西安 710302)



基于有限元原理对建筑基坑边坡支护稳定性的计算研究

刘占宏

(陕西国防工业职业技术学院 建筑与热能分院,陕西 西安 710302)

选取某一实际护坡支护工程进行有限元建模，并采用MATLAB8.0软件以及ANSYS9.0软件找到滑裂面，计算出滑裂面上切应力的数值以及最大切应力的作用位置，再通过有限元法计算出边坡支护稳定性安全系数，并与传统方法计算得出的安全系数进行对比。结果显示：有限元法计算得出的安全系数较大，且几种方法的安全系数变化趋势是相同的。

有限元; 安全系数; 滑裂面; 稳定性

随着国内工程建设的不断增多，许多建设部门都会涉及到大量的边坡问题，边坡一旦发生失稳破坏，将会发生严重危害，因此，把边坡失稳灾害降到最低一直是工程设计人员所不懈追求的目标。鉴于此，本研究拟通过对某实地的有限元建模以探寻建筑工地中人造边坡的稳定性问题，旨在发现其中规律，并将其推广到更广泛的边坡稳定性研究领域之中。

1 有限元建模原理

有限元方法基本求解步骤：根据实际问题确定求解域的几何区域；将求解域划分为有限个网格单元的离散域(网格单元越多，计算结果越精确)；推导有限单元的列式，建立单元试函数，进而形成单元矩阵；采取迭代法或者直接法等对联立方程组进行求解，获得单元节点处状态变量近似值。单元的各种性质是根据单元位移来建立的，假设单元位移分量由坐标线性函数表示，单元应变为：

{ε}=[εxεyεxy]T

(1)

根据广义的胡克定律，针对线弹性提来说，单元应变分量{ε}与单元应力分量[σ]存在线性关系：

[σ]=[D]{ε}=[D][B]{δ}e

(2)

在公式(2)中，[D]为弹性矩阵，仅与材料性质有关，在平面应力状况下为：

(3)

{F}e=∬[B]T{δ}tdxdy=∬[B]T[D][B]tdxdy{δ}e=[k]{δ}e

(4)

其中，[K]为单元刚度矩阵，结合公式(4)可知

[K]=∬[B]T[D][B]tdxdy

(5)

单元分析完毕之后，即可结合结构力学方法组合所有单元特征，推导出整个单元体系的性质，这一过程被称为总体分析。结合公式(5)，将结点i的平衡方程，集合结构各个结点对应的平衡方程，得到整体结构的平衡方程为：

[K]{δ}={R}

(6)

采用有限元法进行边坡稳定的分析与传统极限平衡法相比，主要具备以下优势：能够充分考虑到土体本构的非线性关系作为边坡稳定性分析的基础；可适应复杂多变的边坡条件，例如存在结构物作用以及支护、几何形状复杂的边坡。

2 基于有限元法的安全系数计算

结合宝鸡市一在建民用住宅楼护坡支护工程实际情况，根据经验可知边坡发生失稳破坏的主要方式为在塑性区形成一个滑裂带(见图1)。

图1 边坡失稳滑裂带分布Fig.1 Distribution of slope failure zone

(7)

结合摩尔库伦准则可知，抗剪强度τf与正应力σ间存在如下关系：

τf=σtanφ+c

(8)

因此整个滑动面安全系数为：

(9)

结合有限元原理可知，边坡破坏是一个渐进的过程，破坏区域从一点开始面，逐步拓展到全局，土体应力时刻变化，直到失稳破坏，在边坡沿某一滑动面达到极限平衡条件发生破坏时，对滑动面上每一点均有：

τ=τf/F

(10)

图2 微元体受力图Fig.2 Infinitesimal body diagram

根据力的平衡条件可知

Ti+Ri=0

(11)

即有：

(12)

其中Δli为微元曲线长度，那么结合微积分基本思想可知，针对整个曲面则有：

(13)

进一步可得：

F=∫lτfdl/∫lτdl

(14)

在公式(14)中F即为安全系数。

针对本研究实际问题，假设如图3所示边坡土体ABC为脱离体。

图3 滑动体受力示意图Fig.3 Schematic diagram of force of sliding body

在图3中，边坡应力分布为σij(x,y)，滑裂面正应力为σ，剪应力为τ，脱离体受到外力σ与τ合力平衡，则在滑裂面上可由摩尔—库伦准则得到如下公式：

(15)

(16)

3 算例分析

3.1 计算流程设计

选取宝鸡市某一施工基坑，支护方式为护坡支护，具体力学参数为：土容重γ=19.60kN/m3、坡角θ=45°、坡高h=20m、内摩擦角φ=20°、弹性模量E=2.8×107Pa、粘聚力c=22.5kPa、泊松比μ=0.3，坡体底边固定约束，左右边界水平约束，见图4。

图4 约束条件示意图Fig.4 Sketch map of constraint condition

结合有限元原理，研究按照较密的划分原则对图4进行网格划分(见图5)，结点总数3 925个，单元总数为2 431个。

图5 网格划分Fig.5 Grid division

借助MATLAB8.0软件以及ANSYS9.0软件对其进行计算，计算流程见图6。

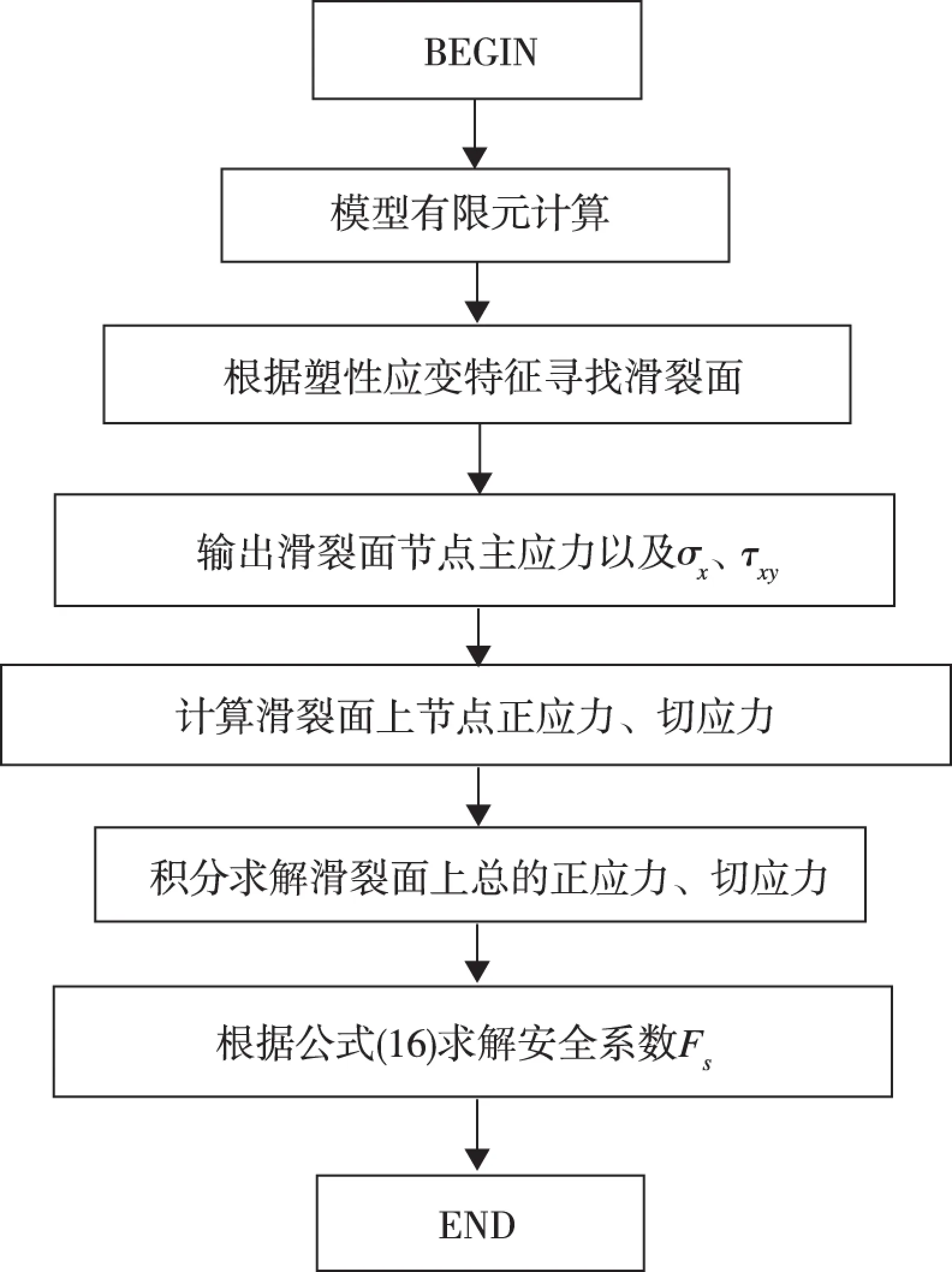
图6 滑裂面与安全系数计算流程图Fig.6 Flow chart of calculation of slip surface and safety factor

3.2 计算结果与结构分析

3.2.1 滑裂面位置确定以及滑裂面切应力分析

在有限元计算过程中，自重等级分30个等级匀速加载，结合ANSYS9.0软件计算塑性区塑性应变等值曲线(见图7)，其中红线位置为边坡最危险滑动面，并得到最危险滑动面的拟合曲线(图8(A))以及各节点对应的切应力数据(图8(B))。

图7 塑性应变等值线与最危险滑动面Fig.7 Plastic strain contour and the most dangerous slip surface

图8 滑裂面曲线拟合以及滑裂面切应力拟合Fig.8 Curve fitting of slip surface and fitting of the shear stress on the slip surface

由图8(A)可知滑裂面近似于圆弧，与滑裂面为圆弧假设具有一致性，结合图8(B)的拟合曲线可算出滑裂面上的每一处所对应的切应力，其最大切应力大概在结点4、5、6之间，因此在实际工程护坡设计中，要保障最大切应力处符合设计要求，以免发生护坡失稳滑裂破坏。

3.2.2 安全系数的计算及对比分析

影响边坡稳定的参数有许多，分别选取2个参数为变量(坡角θ、粘聚力c)，根据图6中的程序流程图，进行ANSYS程序设计，计算了每个参数变化情况下的安全系数值，并与传统的瑞典法、毕肖普法、简布法进行对比分析，结果见表1和表2。

表1 坡角θ为变量(H=20m、φ=20°、c=22.6kPa)

表2 粘聚力c为变量(H=20m、φ=20°、θ=45°)

由表1和表2可知：几种方法得出的安全系数变化趋势都是一致的，说明了该研究计算方法科学且有效。此外，采取有限元法寻找滑裂面得到的安全系数比传统的瑞典法、毕肖普法、简布法计算所得安全系数值要大，究其缘由，可能是传统的瑞典法、毕肖普法以及简布法加入了过多假设，钢化了坡体结构，造成计算结果偏于保守，而采取有限元法寻找滑裂面由于更加接近实际工程情况，从而使得计算结果更加精确。

4 结论

1)滑裂面切应力近似于抛物线(见图8)，最大切应力产生在滑裂面中间位置(节点4、5、6)，在实际工程中，若护坡底部产生细微隆起，实际产生滑动位置为护坡中部位置，要注意对护坡中部加强锚杆锁固，加大约束力度。

2)有限元法研究安全系数偏大，这是由于有限元法更加贴近实际，传统方法钢化了坡体结构。因此，在实际护坡支护过程中，可根据有限元计算结果适当简化支护方案。

3)目前有限元原理在建筑基坑边坡支护稳定性的计算方面还不够成熟，本研究将有限元法融入到边坡支护的计算中，可为日后的支护方案设计提供了新的计算思路。

[1] 赵杰.边坡稳定有限元分析方法中若干应用问题研究[D/OL].大连理工,2006:28[2016-05-20].http://www.cnki.net/KCMS/detail/detail.aspx?.

[2] 常崇义.有限元轮轨滚动接触理论及其应用研究[D/OL].中国铁道科学研究院,2010:10-14[2016-5-16].http://www.cnki.net/KCMS/detail/detail.aspx?.

[3] 邓岳保.竖井地基固结解析理论与有限元分析[D/OL].浙江大学,2013:37-39[2016-5-12].http://www.cnki.net/KCMS/detail/detail.aspx?.

[4] 赵建军.公路边坡稳定性快速评价方法及应用研究[D/OL].成都理工大学,2007:12-13[2016-4-26].http://www.cnki.net/KCMS/detail/detail.aspx?.

[5] 倪卫达.基于岩土体动态劣化的边坡时变稳定性研究[D/OL].中国地质大学,2014:46-49[2016-5-18].http://www.cnki.net/KCMS/detail/detail.aspx?.

[6] 孙志彬.边坡稳定性上限分析方法及参数反演研究[D/OL].中南大学,2013:36-38[2016-5-25].http://www.cnki.net/KCMS/detail/detail.aspx?.

[7] 吴振君,王水林,汤华,等.一种新的边坡稳定性因素敏感性分析方法—可靠度分析方[J].岩石力学与工程学报,2010,29(10):2050-2055.

[8] 黄润秋.岩石高边坡发育的动力过程及其稳定性控制[J].岩石力学与工程学报,2008,27(8):1525-1544.

[9] 邓东平,李亮.基于滑动面搜索新方法对地震作用下边坡稳定性拟静力分析[J].岩石力学与工程学报,2012,31(1):86-98.

[10]HISHAM T,EID K H,RABIE D W.Drained residual shear strength at effective normal stresses relevant to soil slope stability analyses[J].Engineering Geology,2016,38(11):106-112.

[11]LARISA B L.Domain decomposition finite element/finite difference method for the conductivity reconstruction in a hyperbolic equation[J].Communications in Nonlinear Science and Numerical Simulation,2016,5(12):83-86.

[12]DANIEL J E,ELENA B F,JAIME C G,et al.Decision aid system founded on nonlinear valuation,dispersion-based weighting and correlative aggregation for wire rope selection in slope stability cable nets[J].Expert Systems With Applications,2016,76(5):121-126.

[13]VAFAEIAN B,LE L H,TRAN N H T,et al.Micro-scale finite element modeling of ultrasound propagation in aluminum trabecular bone-mimicking phantoms:A comparison between numerical simulation and experimental results[J].Ultrasonics,2016,4(7):35-37.

[14]HONG F F,GUO H,HOU J,et al.A stabilized mixed finite element method for steady and unsteady reaction-diffusion equations[J].Computer Methods in Applied Mechanics and Engineering,2016,48(5):52-58.

Stability calculation of slope support in building foundation pit based on finite element theory

LIU Zhanhong

(Shaanxi institute of Technology Architecture and Thermal Energy Branch, Xi'an, Shaanxi 710302,China)

Based on a practical slope supporting engineering for finite element modeling, we applied MATLAB8.0 software and ANSYS9.0 software to found slip surface, calculated slip surface shear force value and maximum shear force position. Then, calculated supporting the stability of the slope safety coefficient by the finite element method, and compared with the traditional method. The results showed that the safety factor calculated by the finite element method was larger, and the change trend of the safety factor of several methods was the same.

finite element; safety factor; slip surface; stability

1004—5570(2016)06-0093-05

2016-06-04

刘占宏(1977-),男,讲师,研究方向:土木工程技术,E-mail:137477424@qq.com.

TU470

A