一种线性约束连续自适应方向图控制方法*

邓 欣

(中国西南电子技术研究所,成都 610036)



一种线性约束连续自适应方向图控制方法*

邓 欣**

(中国西南电子技术研究所,成都 610036)

针对任意阵列天线的自适应空域滤波和低副瓣控制的问题，提出了一种连续自适应方向图控制方法。该方法通过采用线性约束最小方差准则的方向图综合算法(LCMV-PS)产生具有低副瓣特性的静态权矢量，利用该权矢量构造出新的约束条件，进行线性约束最小均方误差(LMS)自适应波束形成。该方法避免了常规的线性约束最小方差(LCMV)算法的矩阵求逆运算，计算复杂度低。对几种天线阵形的计算机仿真结果表明该方法收敛速度快，稳态性能良好。

阵列信号处理；自适应波束形成；方向图控制；最小均方算法

1 引 言

近几十年来，自适应阵列处理已广泛应用于雷达、通信、电子对抗、导航等众多领域。自适应阵列处理可以在保证天线波束主瓣对准期望信号方向的同时，在未知干扰方向自适应地形成零陷以抑制干扰。自适应处理算法[1-3]均需要累积足够多的快拍数据[4]或一定的响应时间[5]才能得到最优权矢量，而对于随时间快变的干扰则无法及时响应和在干扰方向形成零陷，且由于副瓣电平较高，天线系统易受强干扰的影响。

阵列的低副瓣处理是应对这类突发干扰的一种有效方法。在获得低副瓣或复杂方向图的方向图综合方面的研究成果中，Dolph首次提出的Dolph-Chebyshev方向图综合方法及一系列改进方法[6-7]，可得到在限定最大副瓣电平条件下的最优权矢量，但该方法只能用于均匀等距阵列，而不适用于非均匀阵设计。文献[8]提出的静态方向图数值综合算法(Numerical Quiescent Pattern Synthesis,NPS)可适用于任意阵和复杂方向图设计，但迭代次数多，运算量大。文献[9-10]提出的基于线性约束最小方差准则的方向图综合方法(Linearly Constrained Minimum Variance Pattern Synthesis,LCMV-PS)，相对于NPS算法具有较小的迭代次数和更好的收敛性。

以上列举的方向图综合方法适用于阵列训练数据中只含有空间独立白噪声的情况，对阵列接收数据中的干扰信号不具有抑制作用。对于一些自适应处理算法，如线性约束最小方差(Linearly Constrained Minimum Variance,LCMV)波束形成器[3]的最优权矢量，无法通过与方向图综合的最优权矢量直接点乘的方式得到自适应方向图的低副瓣结果。文献[11]提出的基于LCMV波束形成器的自适应方向图控制方法，需要累积足够多的采样数据，且涉及对数据协方差矩阵的求逆运算，计算量大。为此，本文提出了一种适用于任意阵列的连续自适应方向图控制方法，使得阵列方向图具有期望的低副瓣特性和良好的干扰抑制能力，且计算复杂度低，稳态性能良好。

2 基于线性约束最小方差准则的静态方向图综合方法[9]

线性约束最小方差波束形成器[3]的数学表达式为

wopt=argminwHRXws.t.CHw=f。

(1)

式中：H表示矩阵共轭转置；RX=E[X(k)XH(k)]为阵列接收数据的协方差矩阵；C为约束矩阵；f为约束向量。

式(1)的最优解为

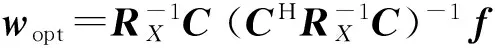
(2)

在一定的应用背景下，要求自适应阵列具有一些特定的方向图特性，如不考虑对阵列接收数据的自适应干扰抑制，由静态方向图综合方法可得到确知波束形成的静态权矢量。

其中基于线性约束最小方差准则的静态方向图综合方法，在阵列方向图的旁瓣区设置多个虚拟干扰，以主瓣宽度作为限定条件，通过迭代运算寻找方向图的最大主副瓣电平比对应的最优权矢量，不但可获得在固定主瓣宽度下最低副瓣电平，而且其迭代系数对方向图的综合条件不敏感，收敛速度快。

假设有Q个具有适当功率的虚拟人工干扰覆盖整个空间区域，其中主瓣区的虚拟干扰功率为0，θq(q=1,2,…,Q)为各虚拟干扰的入射角度。控制虚拟干扰功率的迭代公式表示为

(3)

式中：εq(n)为第n次迭代在方向θq上的干扰功率；g为迭代系数；G(θq,n)为在方向θq上的增益。

上式只针对均匀旁瓣的情况，如要形成具有任意旁瓣电平包络特性的方向图，则需将式(3)稍作修改为

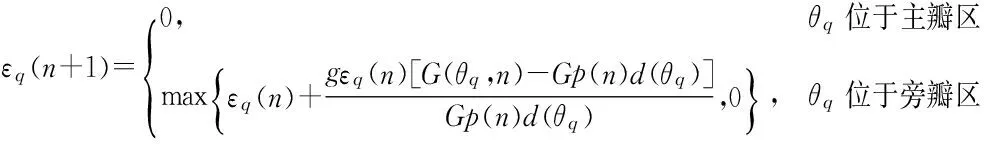
(4)

式中：d(θq)为在旁瓣区θq方位上期望的旁瓣电压。

构造第n次迭代的阵列协方差矩阵为

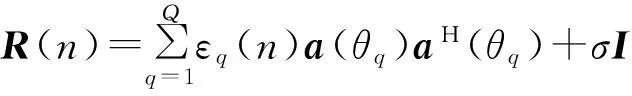
(5)

式中：σI为防止R(n)病态引入的；I是单位阵。

将式(1)的LCMV波束形成器的约束条件设为wHa(θ0)=1，其中θ0为期望信号方位，则由LCMV波束形成器求得每次迭代的最优权矢量为

wopt(n)=R-1(n)a(θ0)[aH(θ0)R-1(n)a(θ0)]-1。

(6)

当迭代趋于收敛，即相邻两次迭代的εq(n)差值小于设定的很小的常数，或方向图已满足期望的方向图特性要求时，迭代结束。

3 线性约束连续自适应方向图控制方法

3.1 方法介绍

LCMV-PS算法得出的最优权矢量是满足特定方向图要求的静态权矢量，但对于天线阵列实际接收信号中的干扰无法自适应形成零陷而滤除。因此,本文提出一种连续自适应方向图控制方法，根据LCMV-PS算法得到的静态权矢量，将阵列接收的有限次快拍数据采用线性约束最小均方误差(Least Mean Square，LMS)自适应处理，计算出既可实现自适应干扰抑制又满足期望方向图特性的任意阵列最优权矢量。

设采用LCMV-PS算法计算出的静态方向图最优权矢量为wps，对于式(1)构造新的约束条件:

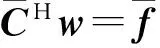
(7)

其中:

(8)

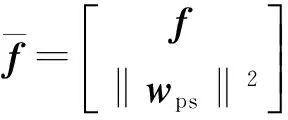
(9)

考虑在实际工程应用中，需要对阵列接收的快拍数据进行实时响应和快速处理，本文采用LMS连续处理算法，递归收敛得到自适应方向图控制的最优权矢量。

我们采用拉格朗日代价函数

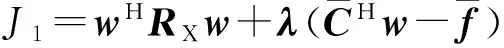
(10)

式中：λ为拉格朗日算子。为了使式(10)关于w最小，对w采用梯度方向搜索，递归表达式为

w(k+1)=w(k)-μwwJ1。

(11)

式中：μw为步长因子，控制递归的收敛速度和稳态失调误差。由式(10)对w求导得到wJ1的表达式为

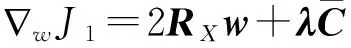
(12)

将式(12)代入式(11)可得

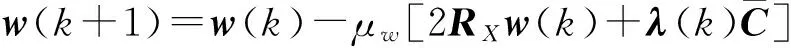
(13)

式中:λ(k)需要在每次递归中更新。由于w(k+1)同样需要满足式(7)的约束条件，可得λ(k)的计算式为

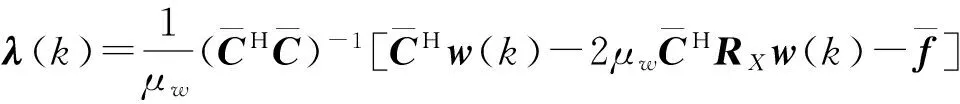
(14)

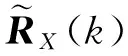
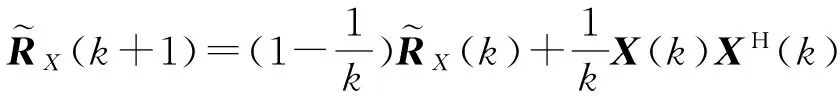
(15)

由此可得到适用于任意阵列的连续自适应方向图控制方法，其具体步骤可总结如下：

步骤1按LCMV-PS静态方向图综合算法计算出所需期望方向图的最优静态权矢量wps；

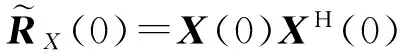
取k=1,2,…

(1)计算

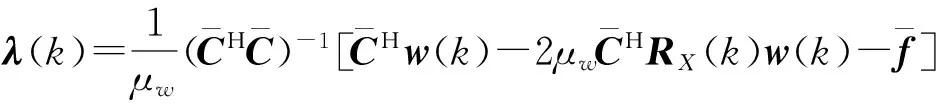
(2)更新权矢量

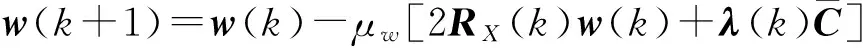
(3)估计阵列协方差矩阵

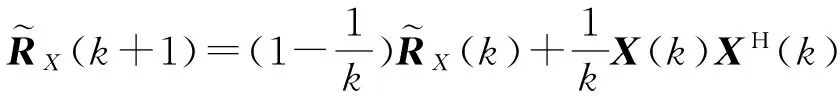
返回步骤1。

在实际工程应用中，可将满足期望方向图特性的静态权矢量wps预先计算并存储，以便于在计算连续自适应方向图控制的最优权时直接调用。

3.2 收敛性分析

计算连续自适应方向图控制的最优权矢量等效为搜索关于天线阵列输出功率wHRXw最小时对应的权矢量，而wHRXw为关于w的二次函数，必然存在全局极小值，因此本文方法的最优权矢量是存在的。但是步长因子μw的选取直接影响连续自适应算法的收敛性，若μw取值太小，则收敛速度太慢；若μw取值过大，则导致稳态失调误差增大，无法收敛到最优值。因此，本文对步长因子μw的选取进行推导分析，得到关于μw取值的约束条件，以确保自适应递归计算的稳态收敛。

关于w在第k次递归的误差矢量为

ew(k)=w(k)-wopt。

(16)

式中：wopt为递归趋于稳态时的最优权矢量。当迭代收敛到最优值时，梯度wJ1=0，将此关系式代入式(12)可得wopt的表达式为

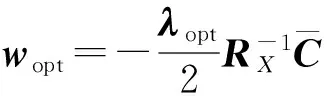
(17)

式中：λopt为最优权矢量wopt对应的拉格朗日算子。

考虑自适应递归计算时误差矢量的变化情况，将式(13)和式(17)代入ew(k+1)的关系式，即有

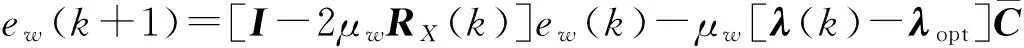
(18)

对ew(k+1)取数学期望，可得到

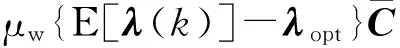
(19)

由式(19)关于误差矢量的递归关系式可看出，本文方法的收敛性取决于I-2μwRX的取值，即μw需满足(I-2μwRX)H(I-2μwRX)的特征值均小于1才能使自适应递归计算收敛至最优值。

4 计算机仿真

为了验证所提方法的有效性，这里以几种均匀阵列和非均匀阵列为例进行仿真计算，并与基于静态方向图数值综合(NPS)[8]的LMS算法(NPS-LMS)、基于LCMV-PS的递归最小二乘[12](Recursive Least Square,RLS)算法(LCMV-PS-RLS)进行比较分析。在以下所有仿真示例中，设定阵列由各向同性的25个阵元组成，期望信号方位为0°，信噪比为0 dB，存在来自-40°方位的非相干干扰，干噪比为20 dB，以及来自50°方位的非相干干扰，干噪比为30 dB，且在30°方位进行固定零点约束。LCMV-PS和NPS算法的常数因子为0.1，迭代次数K=70。连续自适应方向图控制的快拍数为100次。

4.1 例1:均匀线阵情形

阵列为半波长等距线阵，步长因子μw=0.000 01。图1给出了本文方法、NPS-LMS和LCMV-PS-RLS的自适应方向图。从图1可看出几种方法均在-40°、50°和30°形成了较深零陷，且副瓣电平接近-30 dB的设计值。

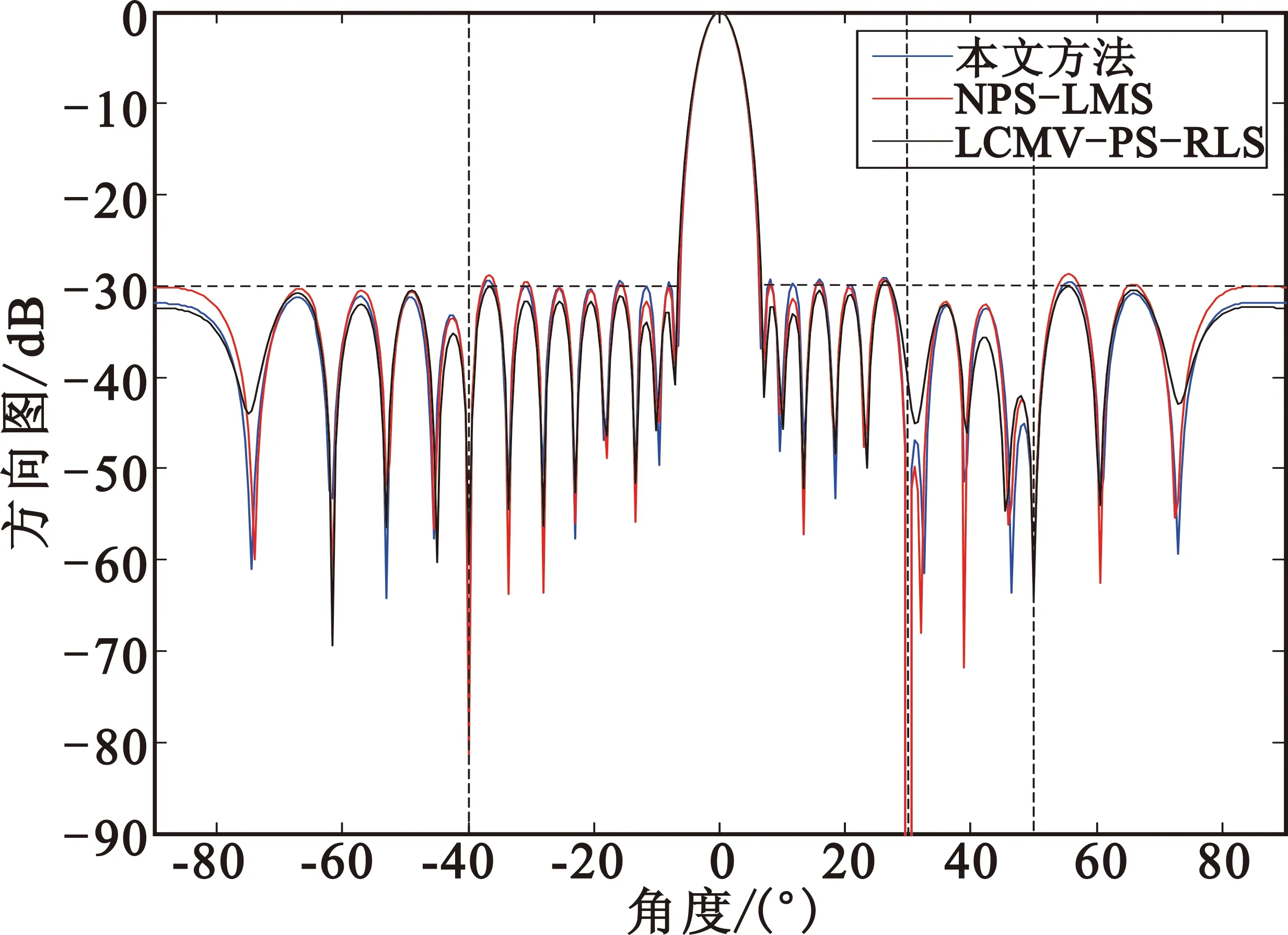
图1 例1的自适应方向图

Fig.1 Adaptive pattern of Example 1

图2为阵列采用本文方法、NPS-LMS和LCMV-PS-RLS的最优权矢量后输出信干噪比随快拍数变化情况，其中本文方法与NPS-LMS均采用LMS连续自适应算法，收敛速度一致，稳态性能与理论值只差0.7 dB左右，且优于LCMV-PS-RLS算法。

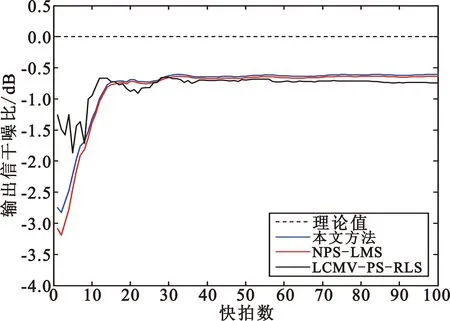
图2 例1的输出信干噪比随快拍数的曲线

Fig.2 Output SINR curve with snapshots of Example 1

4.2 例2:非均匀线阵情形

阵元位置(单位为半波长)为0、0.671 2、1.110 3、1.723 2、2.366 1、2.664 5、3.019 2、3.767 8、4.096 6、4.829 7、5.460 5、6.346 0、6.593 5、7.156 2、7.616 7、7.960 8、8.567 4、8.817 1、9.386 3、9.789 2、10.258 4、10.809 2、11.166 7、11.871 0、11.895 2，步长因子μw=0.000 01，本文方法、NPS-LMS和LCMV-PS-RLS的自适应方向图和输出信干噪比情况分别如图3和图4所示。由图可知，本文方法和NPS-LMS算法的自适应方向图的副瓣电平均较好地满足-21 dB的设计值，虽然NPS-LMS算法的稳态性能略优于本文方法，但其方向图的主瓣已出现严重变形，而LCMV-PS-RLS算法的副瓣已超出期望的副瓣电平，且稳态性能相对较差。

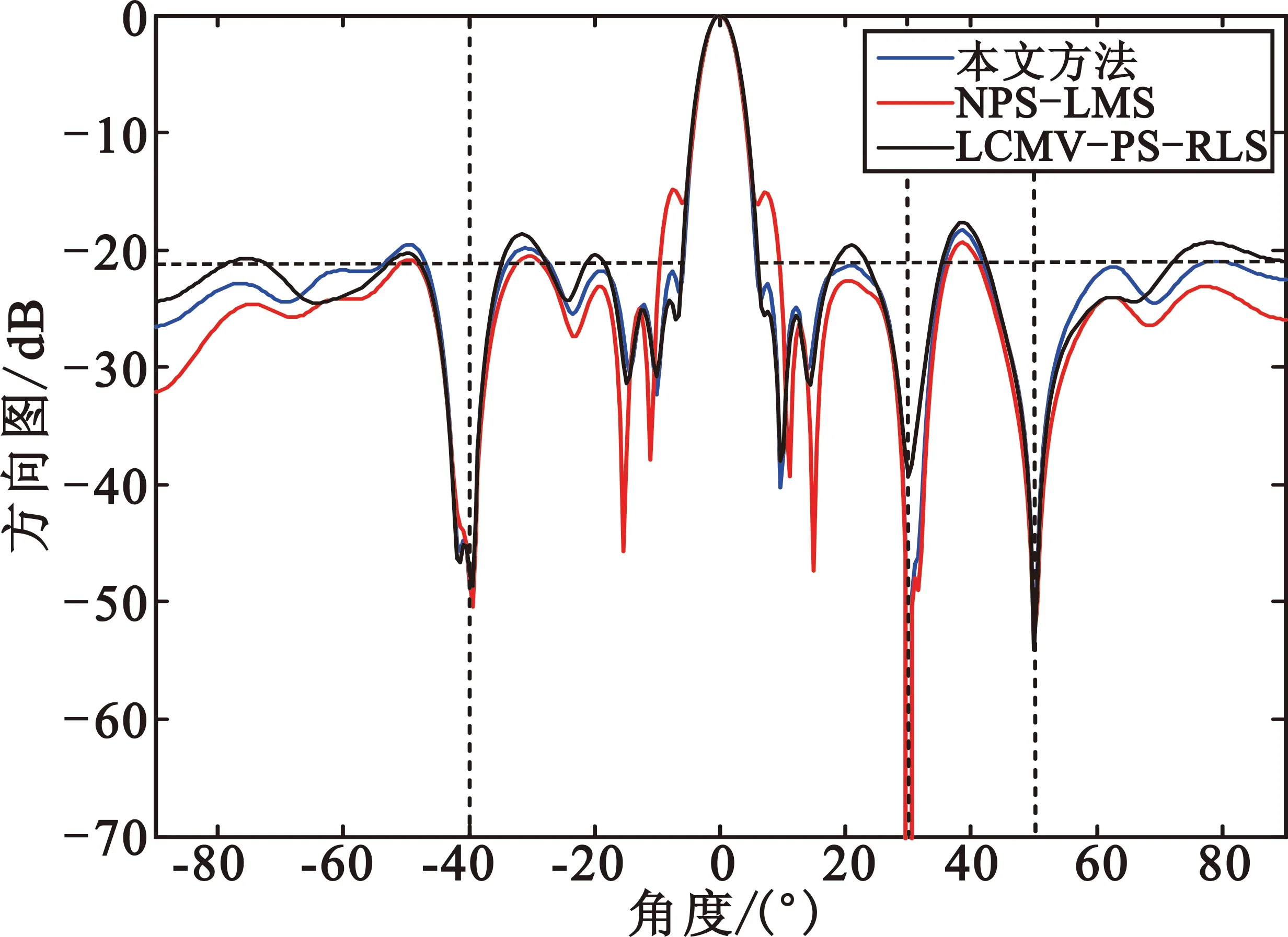
图3 例2的自适应方向图

Fig.3 Adaptive pattern of Example 2

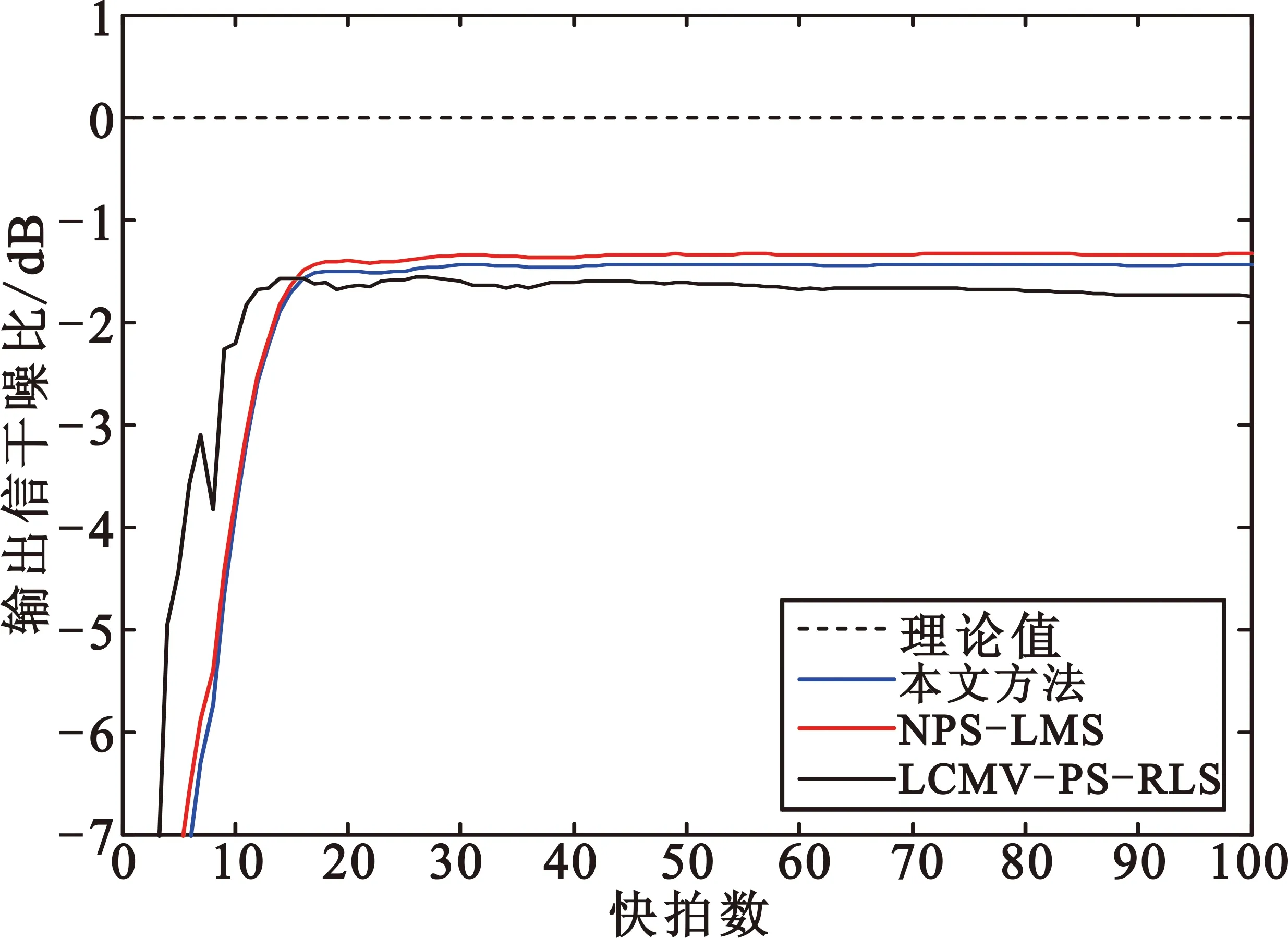
图4 例2的输出信干噪比随快拍数的曲线

Fig.4 Output SINR curve with snapshots of Example 2

4.3 例3：均匀圆阵情形

阵元等距排布成半径为18/π(单位为波长)的均匀圆阵，假定所有入射信号都与阵列共面，因此仅考虑阵列方位面情况。步长因子μw=0.000 01。由图5可看出，本文方法自适应方向图基本满足-18 dB的副瓣电平设计值，且在-40°、50°和30°形成了较深零陷，而LCMV-PS-RLS的方向图在30°的零深相对较浅。在图6的输出信干噪比随快拍数变化的曲线图中，虽然LCMV-PS-RLS的收敛速度较快，但本文方法的稳态性能更加优越，优于其他两种算法。

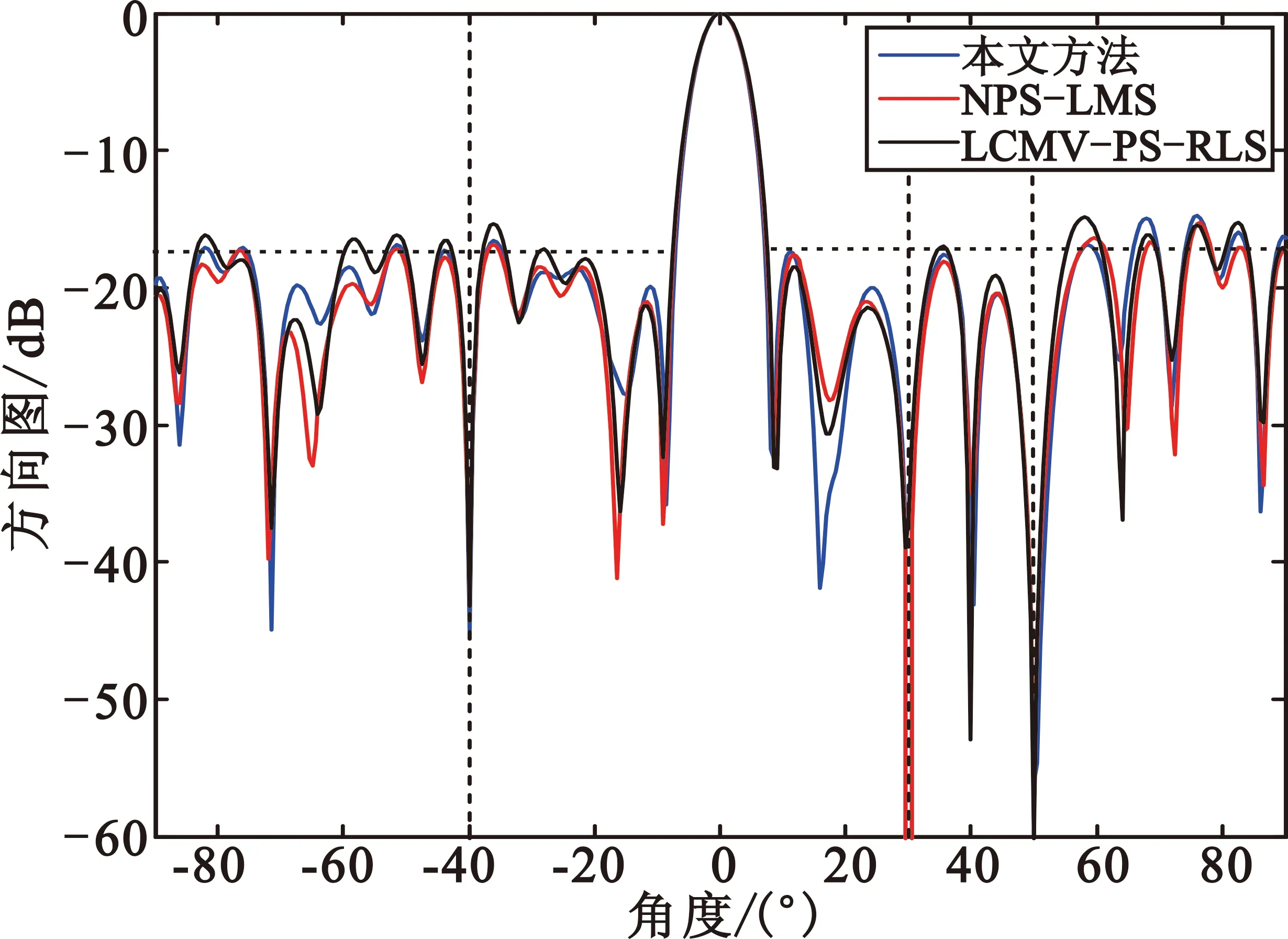
图5 例3的自适应方向图

Fig.5 Adaptive pattern of Example 3

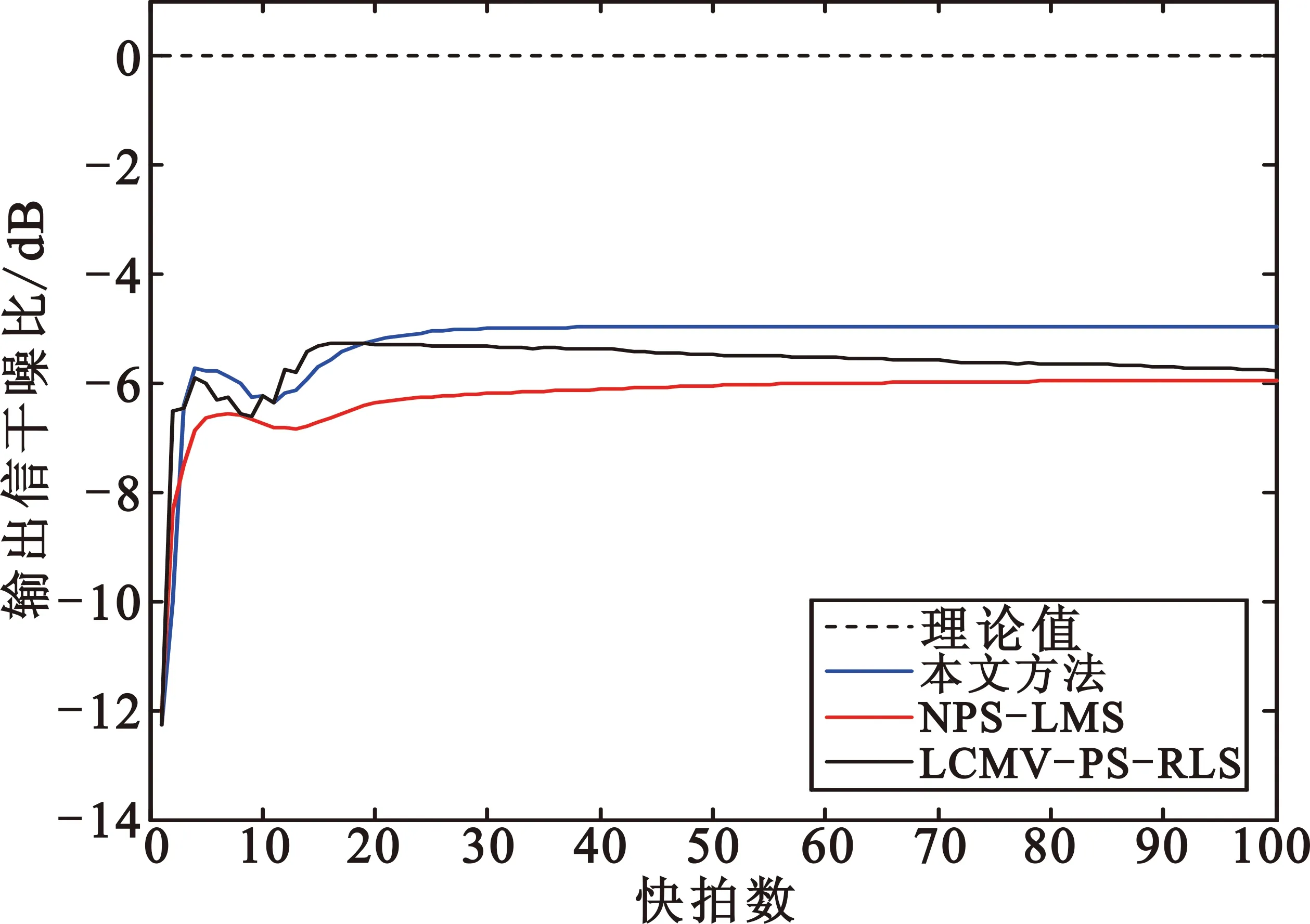
图6 例3的输出信干噪比随快拍数的曲线

Fig.6 Output SINR curve with snapshots of Example 3

4.4 例4:非均匀圆阵情形

阵元在半径为18/π(单位为波长)的圆上随机排布，如图7所示，步长因子μw=0.000 03。由图8可看出，本文方法的副瓣电平满足期望方向图的要求，且在-40°、50°的非相干干扰位置和30°置零位置形成了较深零陷，而LCMV-PS-RLS的副瓣电平高于期望的-18 dB设计值，NPS-LMS的主瓣有所变形，且NPS-LMS和LCMV-PS-RLS在-40°的零深较浅，仅有-35 dB。图9为非均匀圆阵情形下输出信干噪比随快拍数变化的曲线图，可见LCMV-PS-RLS收敛后的稳态性能有所下降，而本文方法的稳态性能优于NPS-LMS算法和LCMV-PS-RLS算法。

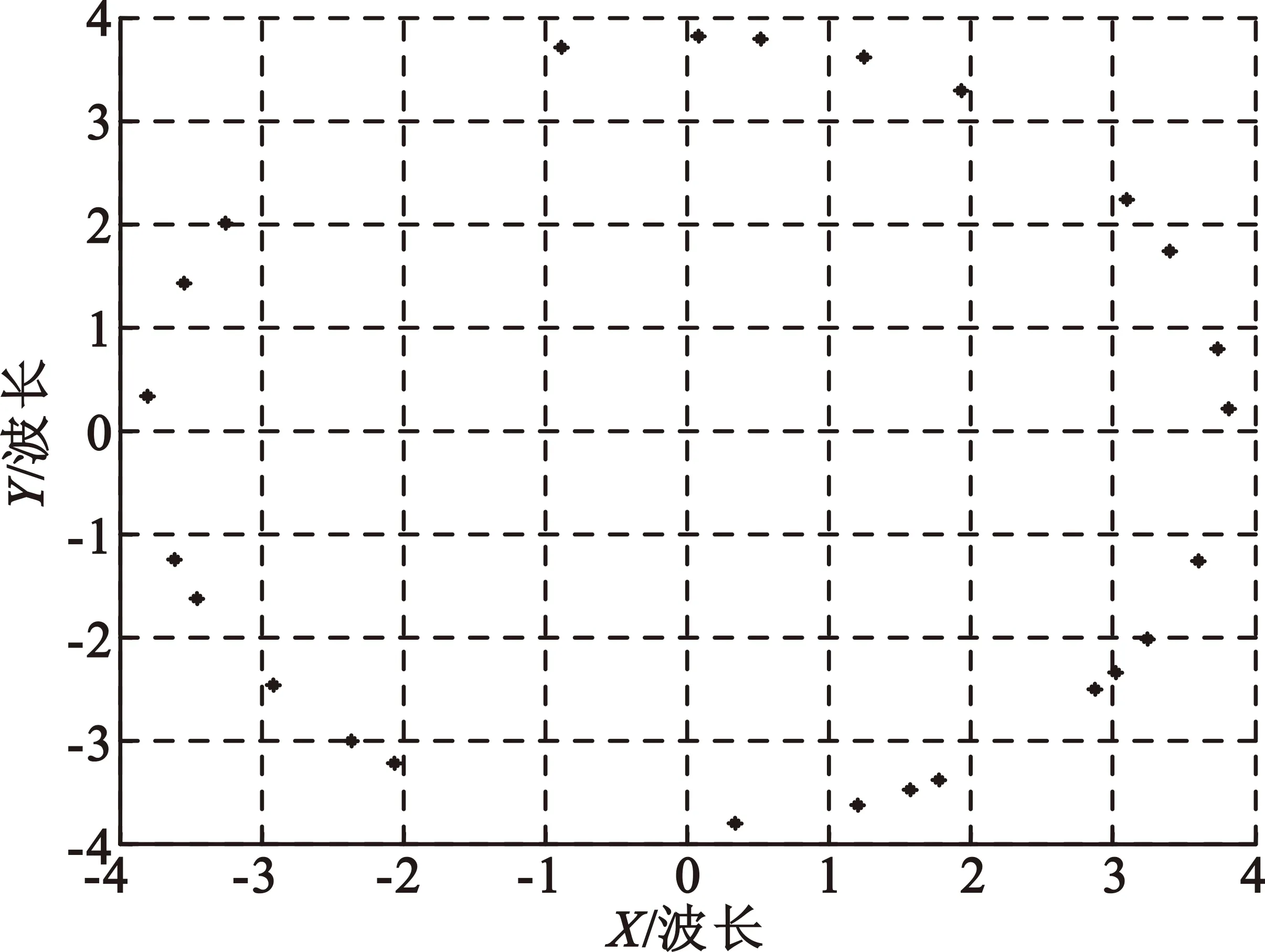
图7 例4中的阵元位置

Fig.7 Array element position of Example 4

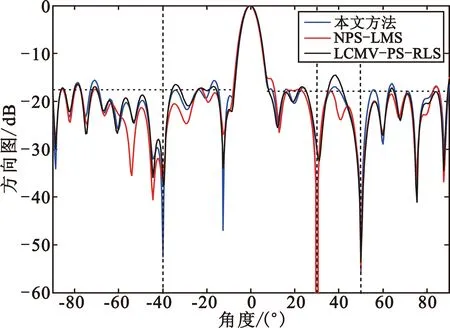
图8 例4的自适应方向图

Fig.8 Adaptive pattern of Example 4

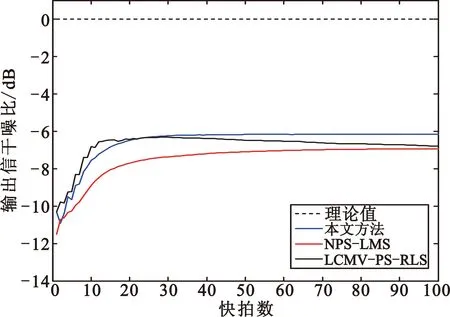
图9 例4的输出信干噪比随快拍数的曲线

Fig.9 Output SINR curve with snapshots of Example 4

由以上的仿真示例可得出：在不同的阵列情形下，相比NPS-LMS算法和LCMV-PS-RLS算法，本文方法收敛速度虽略慢于LCMV-PS-RLS，但稳态性能优越；最优权矢量对应的自适应方向图可满足期望的方向图要求，无主瓣畸变，并在非相干干扰和零点约束位置形成较深零陷，有效抑制来波干扰。

5 结束语

本文提出了一种基于线性约束LMS的连续自适应方向图控制方法。该方法将LCMV-PS算法的静态权矢量用于构造出基于线性约束LMS的新的约束条件，进行自适应波束形成，使天线阵列既具有期望方向图特性还具有自适应干扰抑制的能力。本文方法相对于已有的自适应方向图控制方法，信干噪比损失小且方向图无畸变发生。除此之外，还具有以下优势：可应用于任意阵列；由于阵列方向图的低副瓣特性，使其对时间快变干扰具有一定的抑制作用；采用连续自适应处理，不仅可应用于非平稳环境下的自适应干扰抑制，且避免了矩阵求逆运算，计算复杂度低。通过对几种均匀阵列和非均匀阵列情形的计算机仿真验证了本文方法的有效性。

由于本文方法在非均匀线阵、面阵等情况下的输出信干噪比仍具有一定的损失，因此在提升阵列的稳态性能方面有待进一步研究。

[1] 戴凌燕,王永良,李荣峰.基于不确定集的稳健Capon波束形成算法性能分析[J].电子与信息学报,2009,31(12):2931-2936. DAI Lingyan,WANG Yongliang,LI Rongfeng.Performance analysis of robust Capon beamforming based on uncertainty set[J].Journal of Electronics & Information Technology,2009,31(12):2931-2936.(in Chinese)

[2] 张静宇，王宇，楼大年.一种改进的基于LC-GSC的主瓣干扰抑制方法[J].电讯技术,2014,54(2):163-168. ZHANG Jingyu,WANG Yu,LOU Danian.An improved mainlobe interference suppression method based on generalized sidelobe canceller[J].Telecommunication Engineering,2014,54(2):163-168.(in Chinese)

[3] XU J W,LIAO G H,ZHU S Q.Robust LCMV beamforming based on phase response constraint[J].Electronics Letters,2012,48(20):1304-1306.

[4] STROBACH P.Low-rank adaptive filters[J].IEEE Transactions on Signal Processing,1996,44(12):2932-2947.

[5] FARHANG-BOROUJENY B.Adaptive filters theory and applications[M].Chichester,England:John Wiley & Sons,1998.

[6] BRESLER A D.A new algorithm for calculating the current distributions of Dolph-Chebyshev arrays[J].IEEE Transactions on Antennas and Propagation,1980,28(6):951-952.

[7] TSENG F I,CHENG D K.Optimum scannable planar arrays with an invariant sidelobe level[J].Proceedings of the IEEE,1968,56(11):1771-1778.

[8] OLEN C A,COMPTON R T.A numerical pattern synthesis algorithm for arrays[J].IEEE Transactions on Antennas and Propagation,1990,38(10):1666-1676.

[9] GUO Q H,LIAO G S,WU Y T,et al.Pattern synthesis method for arbitrary arrays based on LCMV criterion[J].IEE Electronics Letters,2003,39(13):1628-1630.

[10] 刘聪锋，廖桂生.改进的快速稳健任意阵列天线方向图综合方法[J].电波科学学报,2009,24(1):104-110. LIU Congfeng,LIAO Guisheng.Improved fast robust pattern synthesis method for arbitrary arrays[J].Chinese Journal of Radio Science,2009,24(1):104-110.(in Chinese)

[11] 苏保伟，王永良，周良柱.基于LCMV线性约束的自适应方向图控制[J].电子与信息学报,2008,30(2):282-285. SU Baowei,WANG Yongliang,ZHOU Liangzhu.A novel adaptive pattern control method based on LCMV[J].Journal of Electronics & Information Technology,2008,30(2):282-285.(in Chinese)

[12] VEGA L R,BENESTY H R J,TRESSENS S.A fast robust recursive least-squares algorithm[J].IEEE Transactions on Signal Processing,2009,57(3):1209-1216.

邓 欣(1982—)，女，陕西汉中人，2007年于西安电子科技大学获硕士学位，现为工程师，主要研究方向为二次雷达和阵列信号处理。

DENG Xin was born in Hanzhong,Shaanxi Province,in 1982.She received the M.S.degree from Xidian University in 2007.She is now an engineer.Her research concerns secondary radar system and array signal processing.

Email:xind829@163.com

A Linearly Constrained Sample-by-Sample Adaptive Pattern Control Method

DENG Xin

(Southwest China Institute of Electronic Technology,Chengdu 610036,China)

For adaptive spatial filtering and low-sidelobe level controlling for arbitrary array,a sample-by-sample adaptive pattern control method is proposed.By adopting Linearly Constrained Minimum Variance Pattern Synthesis(LCMV-PS)，the method achieves a static weight vector,which has the property of low-sidelobe level.The weight vector is used to construct a new constraint,and based on linearly constrained Least Mean Square(LMS) the optimal weight vector of adaptive beamforming is obtained.The method avoids the inverse of the sample covariance matrix,thus enjoying lower computational complexity.Simulations for several kinds of antenna structure demonstrate that the method has a fast convergent rate and better performance than other sample-by-sample pattern control methods.

array signal processing;adaptive beamforming;pattern control;least mean square algorithm

10.3969/j.issn.1001-893x.2016.07.011

邓欣.一种线性约束连续自适应方向图控制方法[J].电讯技术，2016,56(7):777-782.[DENG Xin.A linearly constrained sample-by-sample adaptive pattern control method[J].Telecommunication Engineering,2016,56(7):777-782.]

2015-11-16；

2016-04-20 Received date:2015-11-16；Revised date：2016-04-20

TN911.7

A

1001-893X(2016)07-0777-06

**通信作者：xind829@163.com Corresponding author：xind829@163.com