利用谱估计算法的雷达信号分选*
杨 翔,汪文浩
(1.中航工业北京青云航空仪表有限公司,北京 100017;2.上海交通大学 密西根学院,上海 200240)
利用谱估计算法的雷达信号分选*
杨 翔**1,汪文浩2
(1.中航工业北京青云航空仪表有限公司,北京 100017;2.上海交通大学 密西根学院,上海 200240)
传统雷达信号分选过程中分别进行脉冲重复频率检测与初始到达时间估计时,脉冲搜索时间过长。为此,提出了一种新的基于谱估计的信号分选算法。该算法通过谐波滤除减小了脉冲初始到达时间估计的运算次数,并在进行脉冲重复频率检测的同时估计脉冲初始到达时间,从而避免了传统信号分选算法中对整个序列的遍历,节省了计算资源。仿真结果验证了该算法的有效性。
雷达信号分选;谱估计;脉冲重复频率检测;脉冲初始时间检测;谐波滤除
1 引 言
雷达信号分选是电子侦察信号处理的核心技术,其目的是从侦察接收机侦测到的脉冲流中检测并分离出属于不同辐射源的脉冲序列,为辐射源跟踪、威胁判别与反辐射攻击提供信息。
信号分选由预分选与主分选两部分组成,预分选完成脉冲稀释,主分选完成脉冲重复间隔(Pulse Repetition Interval,PRI)或脉冲重复频率(Pulse Repetition Frequency,PRF)检测和脉冲分离。信号主分选一直是信号分选领域的研究热点和难点[1]。
从20世纪80年代开始,各种关于信号主分选的研究算法相继出现[2-14],主要算法包括到达时间差(Time Difference of Arrival,TDOA)直方图分析算法[2-5]和变换域分析方法[6-7]。TDOA直方图分析算法利用脉冲TDOA统计信息估计各个独立脉冲序列的PRI,变换域分析算法通过分析脉冲到达时间(Time of Arrival,TOA)序列的变换域特征估计各个独立脉冲序列的PRI或PRF。
在完成PRI或PRF检测后,信号分选算法需要在脉冲序列中搜索每一个脉冲串的初始脉冲到达时刻(Initial Arrival Time,IAT),进而完成脉冲串的提取[2-3,8]。IAT搜索往往要耗费大量计算资源,使得信号分选实时性较低。文献[9-10]分别通过研究数据流网格聚类和基于样本的周期估计方法来提高IAT搜索的运算效率,以提高信号分选的实时性。
本文利用谱估计的方法解决IAT搜索耗费大量资源的问题。谱估计算法最早在美国空军专利[11]中提出。此后,文献[7]提出圆周映射谱估计算法,对传统的谱估计进行了一定改进。文献[12]通过调整采样点间隔,实现了对谱估计算法估计精度和运算时间的控制,提高了谱估计算法的信号环境适应性。文献[13]提出首先利用谱估计算法进行粗分选,再利用小波包变换提取特征进行再分选的算法,保证了信号分选的实时性与可靠性。然而,已有的谱估计算法在进行PRF检测时,会检测到大量真实PRF整数倍的虚假PRF;同时,已有的谱估计算法只利用了脉冲TOA序列幅度谱信息,在完成脉冲串PRF检测后,需要进行序列遍历搜索,以检测不同脉冲串的初始到达脉冲,耗费大量资源。
本文从研究脉冲TOA序列的幅度谱与相位谱入手,推导了谱图的理论表示,提出了谐波滤除来剔除虚假PRF以减少IAT估计的运算量,并在利用脉冲幅度谱检测序列PRF的同时,利用谱图的相位信息检测序列的IAT。这种联合PRF检测与IAT估计的方法可有效降低信号分选算法的运算时间,从而提升信号分选的效率。
2 谱估计方法简介
给定TOA序列{tm|m=0,1,…,M-1},令tm=lm·ΔT(lm为正整数,ΔT为量化时间间隔),则原TOA序列可以表示为
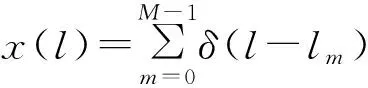
(1)
对x(l)做离散傅里叶变换(DiscreteFourierTransformation,DFT),可得

(2)
式中:L=lM-1。
本文称X(k)为序列{tm|m=0,1,…,M-1}的谱,|X(k)|为序列的幅度谱,∠X(k)为序列的相位谱,k为频率因子。易得,在序列的谱图中,谱值X(k)对应的频率值为k/L。
3 单个稳定PRI脉冲序列的PRF检测与IAT估计
本节将给出利用谱估计算法对单个稳定PRI脉冲序列进行分选的过程。其中,单个稳定脉冲序列是指一个序列中相邻两个脉冲的TOA为一个固定值。
假定一个稳定PRI脉冲序列由M个脉冲的TOA组成,则该TOA序列可以表示为

(3)
式中:s表示IAT;h表示相邻脉冲的TDOA。
对x(l)做DFT,可得

(4)
下面分别利用|X(k)|和∠X(k)检测PRF和估计IAT。
3.1 PRF检测
传统的谱估计算法在生成幅度谱后直接检测峰值[11]。本文对传统的谱估计方法进行改进,在生成幅度谱后对峰值统计量进行谐波滤除。
图1给出了本文算法PRF检测的流程图,其中阴影部分为谐波滤除,为本算法区别于传统PRF检测算法的步骤。谐波滤除时,遍历当前峰值所对应频率因子的整数倍,将其统计量减去当前峰值。通过谐波滤除,可以剔除虚假的检测值,生成滤除谐波后的幅度谱图,以减小后续IAT估计的次数。

图1 PRF检测流程图
Fig.1 Flowchart of PRF detection
3.2 IAT估计
传统的谱估计算法在完成PRF检测后通过序列搜索的方法进行IAT估计[2-3,8],本文通过相位谱直接进行IAT估计,避免了对整个序列的遍历。
利用θ(k)代表∠X(k),由公式(4)可知,幅度谱峰值处的相位可以表示为
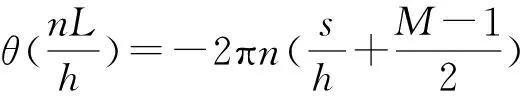
(5)
式中:n为正整数。

需要说明的是,完成DFT后的谱图相位信息存在缠绕的问题,需要采用相位解缠绕方法去除相位模糊。本文所有仿真实验均使用Matlab模拟完成,在傅里叶变换后,利用Matlab自带函数angle提取频域相位,此时相位值会被转换到区间[0,2π)中,然后利用Matlab自带函数unwrap进行解缠绕。
4 复杂脉冲序列的谱估计检测
本节将介绍利用谱估计算法对多个稳定PRI脉冲序列和单个抖动PRI脉冲序列进行分选的过程。
4.1 多个稳定脉冲序列
假定一个脉冲串由P个稳定PRI脉冲序列组成,则这个脉冲串TOA序列可以表示为

(6)
式中:Mp、sp和hp分别代表第p个脉冲序列的脉冲个数、IAT和PRI;L和M分别代表脉冲串的截止时间与脉冲总数。易得

(7)
考虑接收机具备一定的脉冲分辨能力,能区分出上升/下降沿未完全重叠的脉冲,容易推导出利用3.1节提出的方法进行谐波滤除后,有
|X(kp)|≈Mp。
(8)
对于每个峰值所对应的频率因子kp,其所检测出的PRF为kp/L,0≤p≤P。
在将干扰序列滤除后,可以得到改进后的幅度谱

(9)
仿真实验选取一个由8个稳定脉冲序列组成的脉冲串,其PRF分别为10kHz、38kHz、49kHz、57kHz、80kHz、95kHz、105kHz和300kHz。该脉冲串的原始幅度谱图和经过谐波滤除后的幅度谱图如图2所示。由图可知,在滤除谐波后,可清晰地检测出8个脉冲串的PRF。
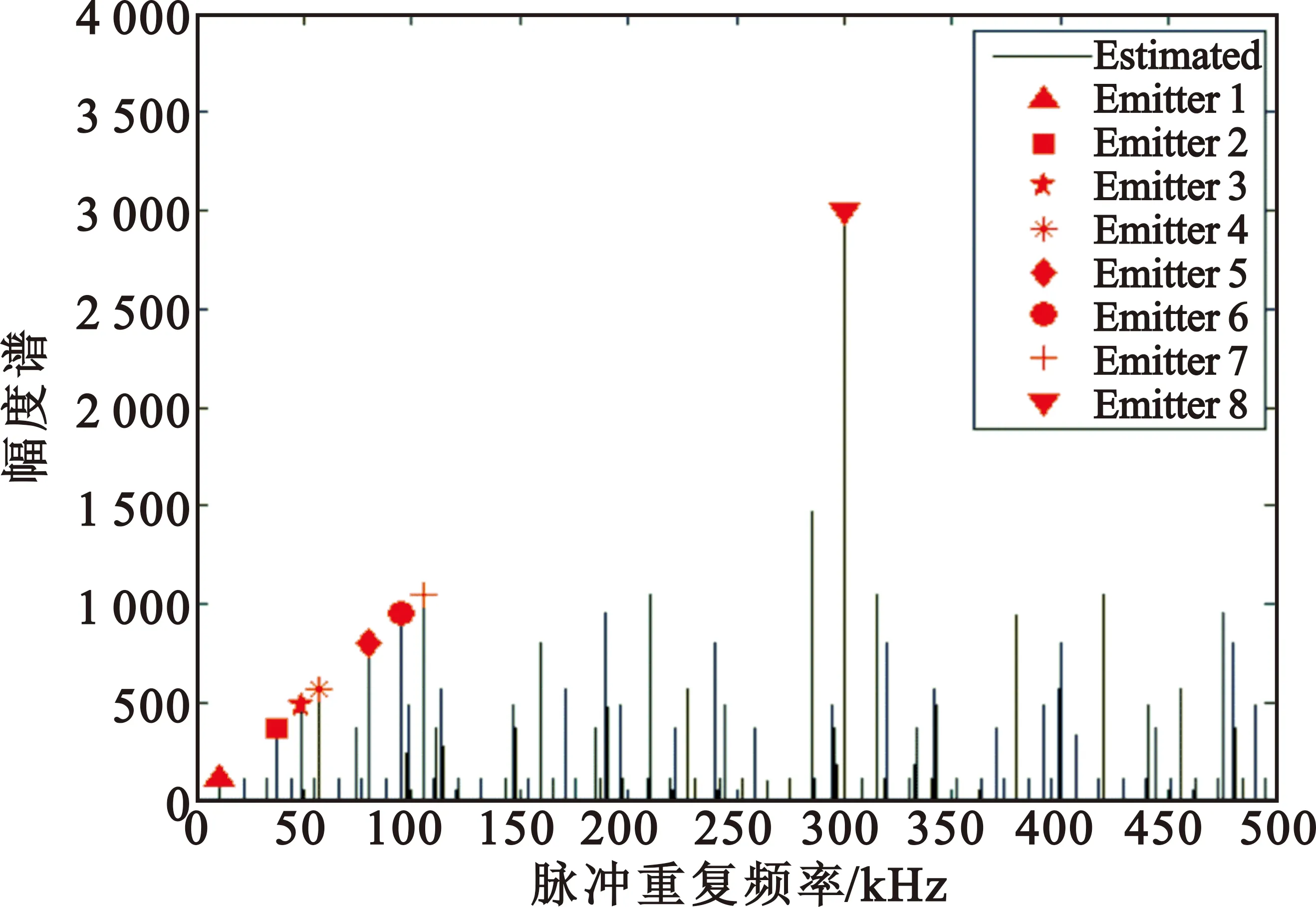
(a)原始谱图
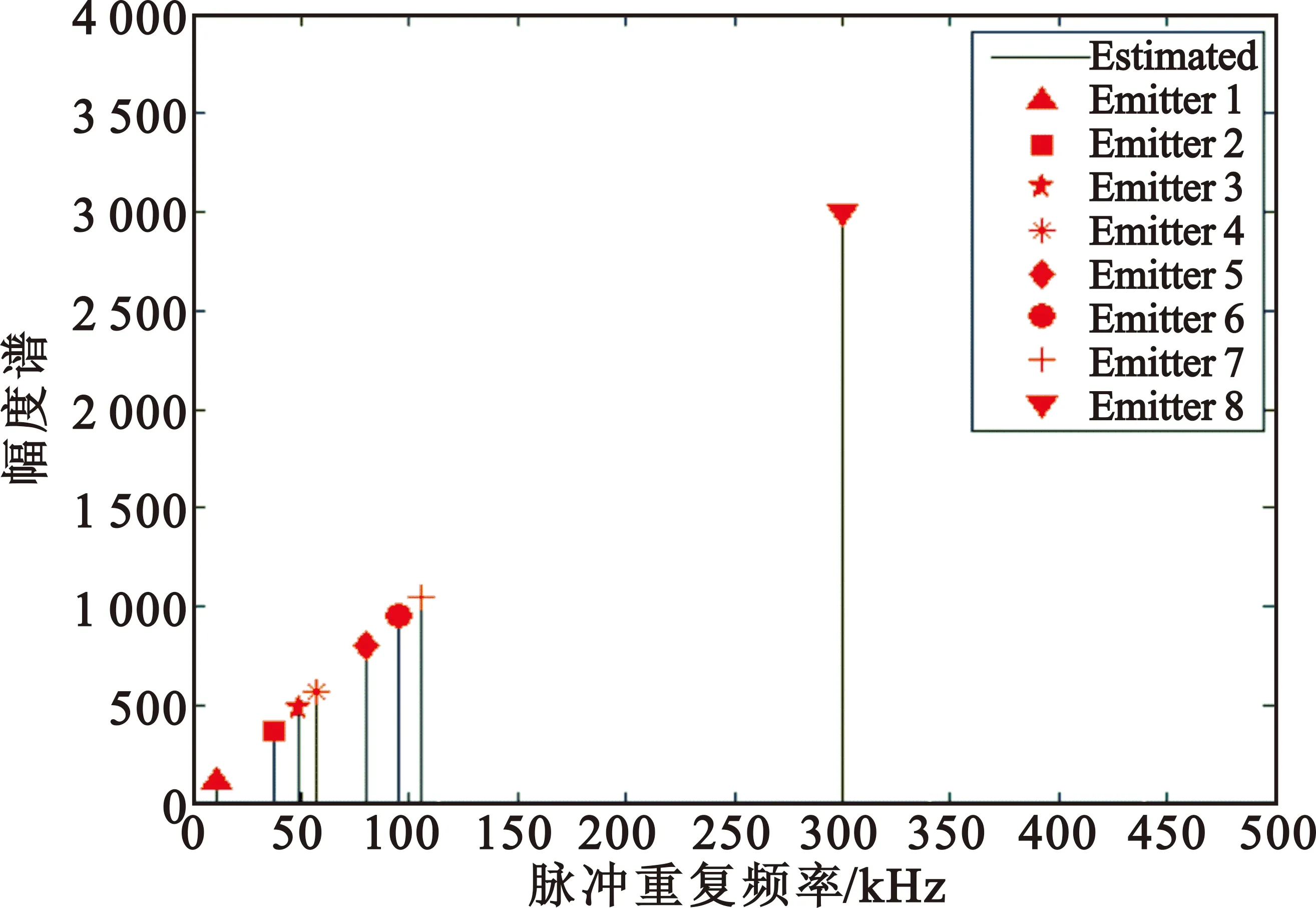
(a)谐波滤除后的谱图
图2 利用幅度谱进行多个稳定PRI脉冲序列的PRF检测
Fig.2PRFdetectionofmultiplestablesequencesbyusingmagnitudespectrum
图3给出了利用相位谱拟合出的直线,可以看到分别对应于辐射源1和辐射源2的相位序列在拟合成直线时分别有一点出现了偏移,这是由于解缠绕时相位值在-π和π处跃迁导致的,并不影响对直线斜率的计算。
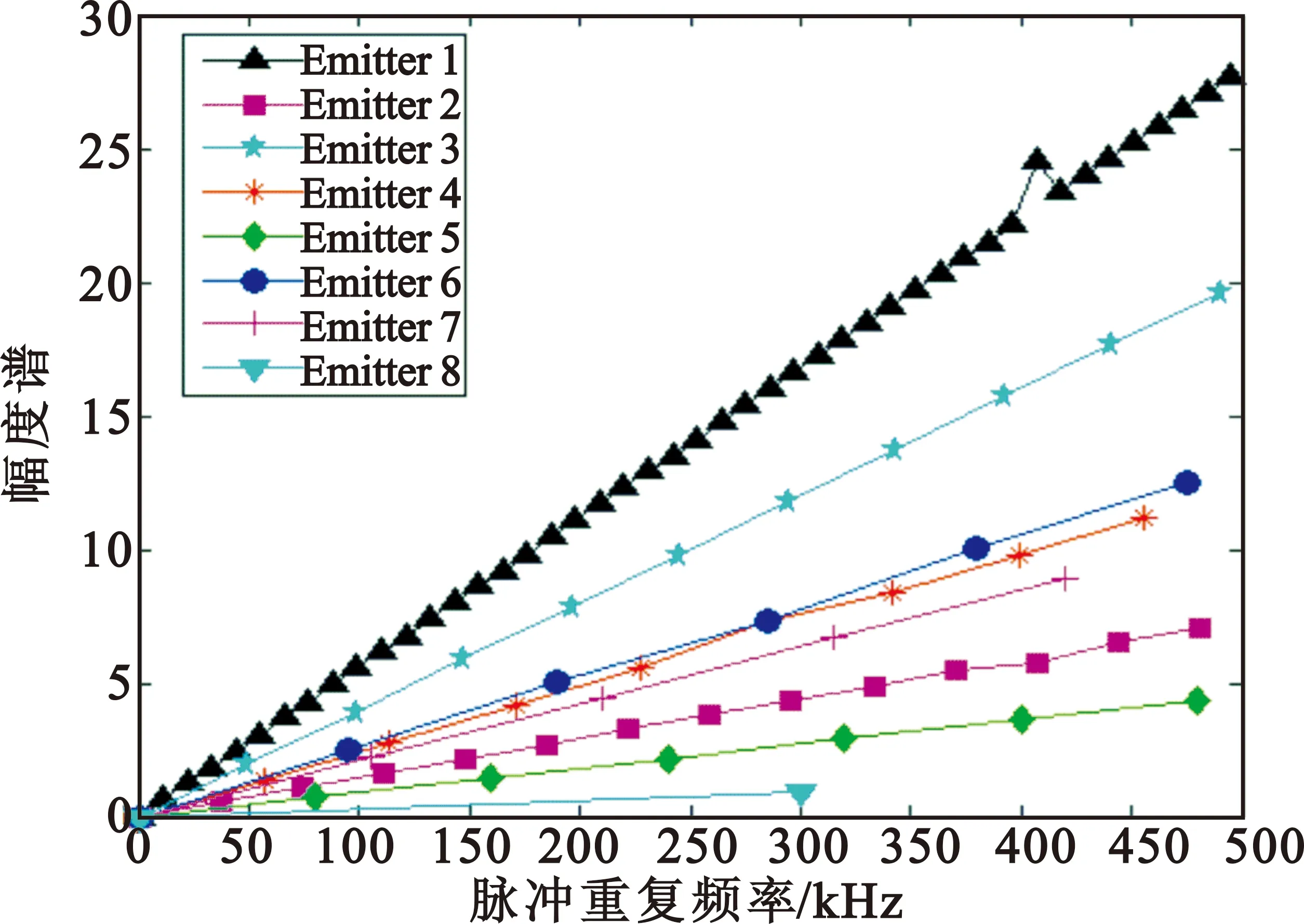
图3 利用相位谱进行多个稳定PRI脉冲序列的IAT估计
Fig.3IATestimationofmultiplestablesequencesbyusingphasespectrum
表1给出了原始序列真实的IAT与利用相位谱检测出的IAT。由表可知,利用谱估计法对多个稳定脉冲序列构成的复合脉冲串进行IAT估计的有效性极高。
表1 对多个稳定脉冲序列的初始脉冲检测结果
Tab.1TheestimatedresultforIATofmultiplestablesequences

编号真值/μs检测值/μs18.895808.9404022.342902.3178036.379306.3793043.906703.9234051.441701.4416064.191904.1823073.373203.3736080.480490.48066
4.2 单个抖动脉冲序列
一般地,用来表示抖动脉冲序列的模型被称为随机差分模型(Random Difference Model,RDM)[15]。本节将以RDM模型为例,给出利用谱估计算法对单个抖动脉冲序列的分选步骤。
假定一个抖动脉冲序列的脉冲重复间隔的中心值为Pj,令tk表示第k个和第k+1个脉冲之间的间隔,则对于RDM模型,有

(10)
式中:U代表均匀分布;ρ代表抖动间隔。
根据RDM模型,容易求得抖动序列的谱为

(11)
式中:h表示原序列的PRI中心值。
为了对序列的谱进行估计,首先推导出序列谱的期望
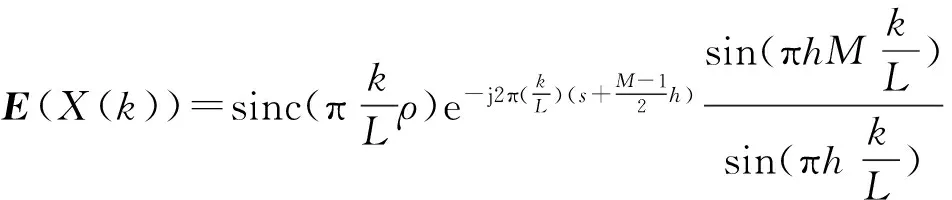
(12)
因篇幅所限,具体的推导过程不再给出,感兴趣的读者可与作者联系。
同时,可以通过对幅度谱方差的推导来估算幅度谱的抖动展宽。详细的推导过程可与作者联系索取。
在实际中,由于发射机和接收机的非线性效应,导致TOA的测量并不准确,使得发射机发射的稳定脉冲序列被接收机接收为抖动脉冲序列。这种测量误差不超过100 ns[16],所引起的序列抖动不超过脉冲序列PRF中心值的1%。
仿真实验选取PRF中心值为105 kHz、初始脉冲到达时间为0.321 7 μs的抖动序列,使抖动序列的抖动分别在PRF中心值(-0.1%,0.1%)、(-0.2%,0.2%)、(-0.5%,0.5%)、(-1%,1%)、(-2%,2%)、(-3%,3%)范围内,可分别对序列进行PRF检测与IAT估计。图4和图5分别给出了脉冲序列的抖动范围在区间(-0.1%,0.1%)和区间(-3%,3%)时,经过谐波滤除后的序列幅度谱。需要指出的是,图5中脉冲序列的幅度谱统计量在谐波对应的频率因子附近出现了负值,这是因为抖动脉冲序列谐波统计量小于基波统计量,在由谐波分量减去基波分量进行谐波滤除时,产生了负值。由图可知,在滤除谐波后,可以清晰地检测出抖动脉冲序列的PRF中心值。
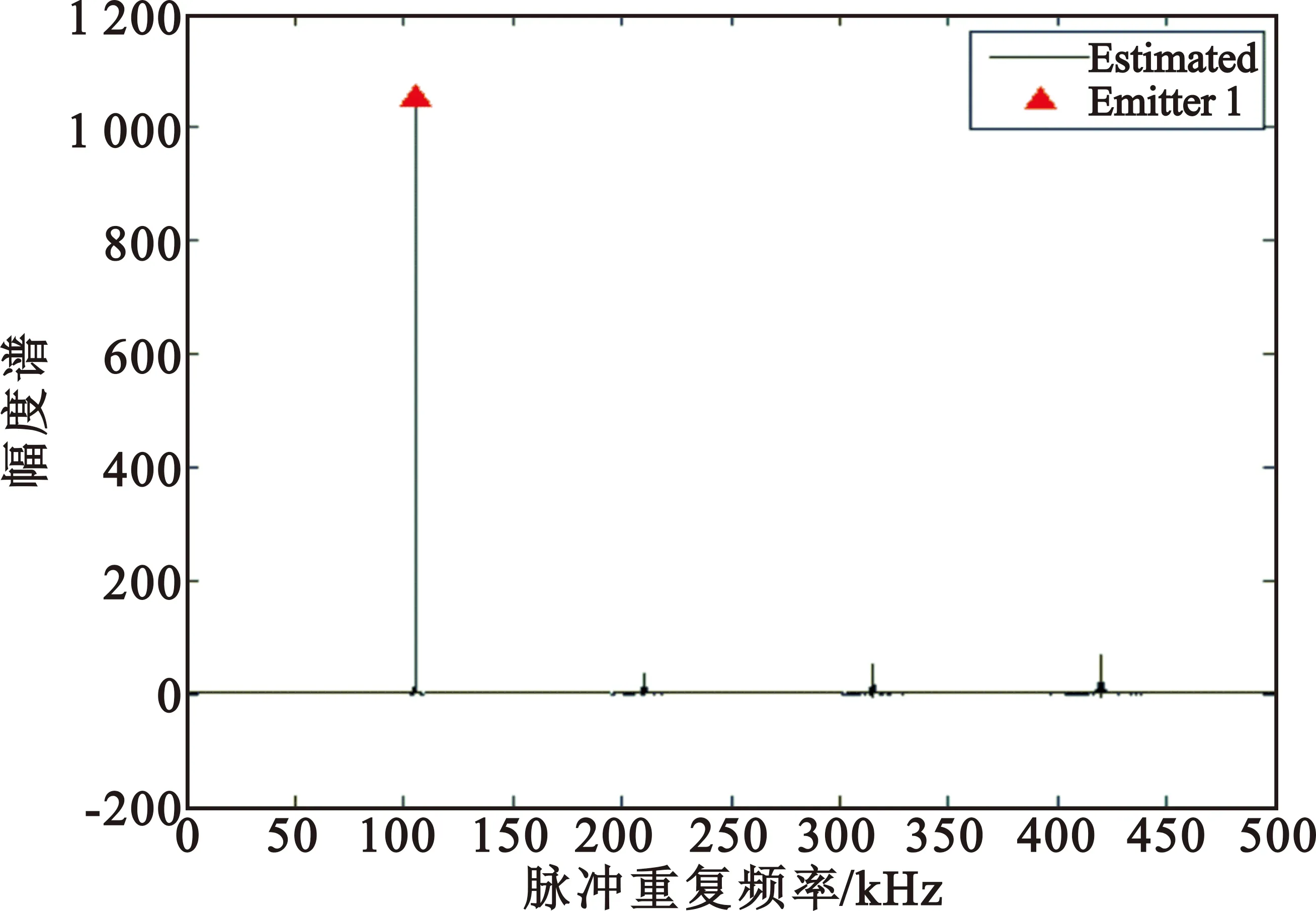
图4 抖动范围在PRF中心值(-0.1%,0.1%)范围内序列滤除谐波后的幅度谱
Fig.4 The magnitude spectrum of jittered sequence with(-0.1%,0.1%) jitter scale after harmonics removed

图5 抖动范围在PRF中心值(-3%,3%)范围内序列滤除谐波后的幅度谱
Fig.5 The magnitude spectrum of jittered sequence with(-3%,3%) jitter scale after harmonics removed
图6和图7分别给出了脉冲序列的抖动范围在区间(-0.1%,0.1%)和区间(-3%,3%)时,利用相位谱拟合出的直线。由图可知,这两条直线与单个稳定PRI脉冲序列相位谱拟合出的直线非常接近,这说明当脉冲序列存在抖动时,依然可以利用脉冲相位谱拟合出直线进性序列IAT估计。

图6 抖动范围在PRF中心值(-0.1%,0.1%)范围内,利用相位谱进行序列IAT估计
Fig.6 IAT estimation of jittered sequence with (-0.1%,0.1%) jitter scale

图7 抖动范围在PRF中心值(-3%,3%)范围内,利用相位谱进行序列IAT估计
Fig.7 IAT estimation of jittered sequence with (-3%,3%) jitter scale
表2给出了当抖动序列的抖动分别在PRF中心值(-0.1%,0.1%)、(-0.2%,0.2%)、(-0.5%,0.5%)、(-1%,1%)、(-2%,2%)和(-3%,3%)范围内时,利用序列的相位谱估计出的IAT。由表可知,利用谱估计法对单个抖动脉冲序列进行IAT估计的有效性较高。
表2 不同抖动范围下估计出的序列IAT
Tab.2 IAT estimation of jittered sequences with different jitter scale

抖动范围/%真值/μs估计值/μs(-0.1,0.1)0.32170.3071(-0.2,0.2)0.32170.2972(-0.5,0.5)0.32170.3031(-1,1)0.32170.2895(-2,2)0.32170.3306(-3,3)0.32170.3635
5 结束语
本文从理论上提出了一种新的利用谱估计进行脉冲去交错的算法,不仅可以高准确度地检测出脉冲序列的PRF,还能同时检测出每一个脉冲序列的IAT,从而完成序列提取。相比于传统信号分选算法需要遍历两次脉冲序列,这种并行检测的处理方法只需要遍历一次脉冲序列,运算效率提升了1倍。本文通过对不同类型的脉冲序列进行仿真实验,验证了该算法在信号分选中的有效性以及运算优势。下一步计划是将本文提出的算法推广到具体的工程应用中。
[1] WILKINSON D R,WATSON A W. Use of metric techniques in ESM data processing[J].IEE Proceedings F:Communications,Radar of Signal Processing,1985,132(4):229-232.
[2] MARDIAH K. New techniques for de-interleaving repetition sequences[J].IEE Proceedings F:Radar and Signal Processing,1989,136(4):149-154.
[3] MILOJEVIC D J,POPOVIC B M. Improved algorithm for deinterleaving of radar pulses[J].IEE Proceedings F:Communications,Radar and Signal Processing,1992,139(1):98-104.
[4] NISHIGUCHI K,KOBAYASHI M. Improved algorithm for estimating pulse repetition[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(2):407-421.
[5] 杨翔,顾洪宇. 基于到达时间差直方图的信号分选算法研究[J]. 电子与信息学报,2015,37(11):2762-2768. YANG Xiang,GU Hongyu. A signal sorting algorithm based on time difference of arrival[J].Journal of Electronics & Information Technology,2015,37(11):2762-2768.(in Chinese)
[6] PERKINS J,COAT I. Pulse train de-interleaving via the Hough transform[C]//Proceedings of 1994 IEEE Conference on Acoustics,Speech,and Signal Processing.Adelaide,Australia:IEEE,1994:197-200.
[7] ORSI R J,MOORE J B,MAHONY R E. Spectrum estimation of interleaved pulse trains[J].IEEE Transactions on Signal Processing,1999,47(6):1646-1653.
[8] WANG P C,ORR M,SPARROW M,et al.System and method for detecting and de-interleaving radar emitters:7397415[P]. 2008-07-08.
[9] 张国毅,王晓峰,张旭洲. 基于数据流聚类的动态信号分选框架[J].电讯技术,2011,51(9):65-68. ZHANG Guoyi,WANG Xiaofeng,ZHANG Xuzhou. A dynamic frame of signal sorting based on data stream clustering[J].Telecommunication Engineering,2011,51(9):65-68.(in Chinese)
[10] 关一夫,张国毅,刘志鹏. 一种基于脉冲样本序列的 PRI 周期信号分选算法[J].电讯技术,2014,54(7):915-920. GUAN Yifu,ZHANG Guoyi,LIU Zhipeng. A novel de-interleaving algorithm for PRI periodic signal based on pulse sample sequence[J].Telecommunication Engineering,2014,54(7):915-920.(in Chinese)
[11] LAVIGNE J P.Wrench:539625[P].1895-05-21.
[12] 李杨寰,初翠强,徐晖,等. 一种新的脉冲重复频率估计方法[J].电子信息对抗技术,2007,22(2):18-22. LI Yanghuan,CHU Cuiqiang,XU Hui,et al.A novel algorithm for estimating pulse repetition frequency[J].Electronic Information Warfare Technology,2007,22(2):18-22.(in Chinese)
[13] 张春杰,王大海.基于脉内特征聚类的分选方法[J].应用科技,2014,41(4):17-21.
ZHANG Chunjie,WANG Dahai. A sorting method for unknown radar emitter signals based on pulse feature clustering[J].Applied Science and Technology,2014,41(4):17-21.(in Chinese)
[14] 蒋锐,朱岱寅,朱兆达. 一种基于等效残差点的InSAR相位解缠绕方法[J].南京航空航天大学学报,2013,45(2):209-216. JIANG Rui,ZHU Daiyin,ZHU Zhaoda. Phase unwrapping approach using equivalent residues for InSAR[J].Journal of Nanjing University of Aeronautics & Astronautics,2013,45(2):209-216.(in Chinese)
[15] VERGARA-DOMINGUEZ L. Analysis of the digital MTI filter with random PRI[J].IEE Proceedings F:Radar and Signal Processing,1993,140(2):129-137.
[16] TSUI J.宽带数字接收机[M].2版.杨小牛,陆安宁,金飚,译.北京:电子工业出版社,2016. TSUI J. Digital techniques for wideband recievers[M].2nd ed.Translated by YANG Xiaoniu,LU Anning,JIN Biao.Beijing:Publishing House of Electronics Industry,2016.(in Chinese)

杨 翔(1989—),女,甘肃定西人,分别于2011年和2014年获北京大学理学学士学位与理学硕士学位,目前主要从事雷达信号分选算法研究;
YANG Xiang was born in Dingxi,Gansu Province,in 1989. She received the B.S. degree and the M.S. degree from Peking University in 2011 and 2014,respectively.Her research concerns radar signal sorting algorithm.
Email:yangxiangyx123@163.com
汪文浩(1995—),男,四川绵阳人,上海交通大学密西根学院学生,主要专业为电子工程。
WANG Wenhao was born in Mianyang,Sichuan Province,in 1995. He is now a student.His major is electronic engineering.
Radar Signal Sorting Based on Spectrum Estimation
YANG Xiang1,WANG Wenhao2
(1.AVIC Beijing Keeven Aviation Instrument Co., Ltd.,Beijing 100017,China;2.University of Michigan,Shanghai Jiaotong University,Shanghai 200240,China)
Traditional radar signal sorting methods have expensive cost on computation in pulse repetition frequency(PRF) detection and initial arrival time(IAT) estimation respectively. To solve this problem,a novel sorting method based on spectrum estimation is proposed. The method cuts down the operational times for IAT estimation by removing the harmonics,and determines the IAT while detecting the periodicity of a pulse train,thus avoiding the conventional traverse of sequence and saving the computational resource. Simulation results demonstrate its feasibility and efficiency.
radar signal sorting;spectral estimation;pulse repetition frequency detection;initial arrival time estimation;harmonics removing
10.3969/j.issn.1001-893x.2016.07.009
杨翔,汪文浩.利用谱估计算法的雷达信号分选[J].电讯技术,2016,56(7):765-770.[YANG Xiang,WANG Wenhao.Radar signal sorting based on spectrum estimation[J].Telecommunication Engineering,2016,56(7):765-770.]
2016-03-17;
2016-07-01 Received date:2016-03-17;Revised date:2016-07-01
TN971
A
1001-893X(2016)07-0765-06
**通信作者:yangxiangyx123@163.com Corresponding author:yangxiangyx123@163.com

