基于空谱特性的高光谱图像压缩感知重构*
陈善学,胡 灿,屈龙瑶
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)
基于空谱特性的高光谱图像压缩感知重构*
陈善学,胡 灿**,屈龙瑶
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)
针对现有的高光谱图像压缩感知重构算法对图像的空谱特性利用不够充分,导致重构图像质量不够高的问题,提出了一种高光谱图像变投影率分块压缩感知结合优化谱间预测重构方案。编码端以频段聚类方式将高光谱图像的所有频段分成参考频段和普通频段,对不同频段单独采用不同精度分块压缩感知以获取高光谱数据。在解码端,参考频段直接采用稀疏度自适应匹配追踪(SAMP)算法重构,对于普通频段,则设计了一种优化谱间预测结合SAMP算法的新模型进行重构:首先通过重构的参考频段双向预测普通频段,并对其进行压缩投影,然后计算预测前后普通频段投影值的残差,最后利用SAMP算法重构该残差,以此修正预测值。实验表明,相比同类算法,该算法充分考虑了高光谱图像的空谱特性,有效改善了重构图像质量,且编码复杂度低,易于硬件实现。
高光谱图像;分块压缩感知;频段聚类;优化谱间预测;稀疏度自适应匹配追踪
1 引 言
压缩感知(Compressed Sensing,CS)理论[1-2]突破了传统信号处理框架的束缚,提供了一种全新的数据采集方式,利用稀疏信号的可压缩性,能够以极少的采样值精确重构原始信号。目前,将压缩感知理论应用于高光谱图像压缩的研究工作已经得到了广泛关注,并提出了相关方案。文献[3-4]提出了高光谱图像的分布式压缩感知重构方法,相比传统的压缩感知算法,减少了编码端测量矩阵尺寸,便于数据存储和计算;文献[5]提出了用三维压缩感知方法来重构视频图像;文献[6]提出了高光谱图像变采样率重构算法,简单利用了谱间信息来提高压缩性能;文献[7]引入了分层贝叶斯模型,提出一种性能较优的基于多任务学习的高光谱图像压缩感知重构算法(Multitask Bayesian CS,MT-Bayes CS);文献[8]提出了一种字典学习结合正交匹配追踪的压缩感知重构算法(K-SVD-OMP),通过构造过完备字典使原始信号能够得到很好的稀疏表示。然而,以上方法均未能充分利用高光谱图像的空谱特性,重构图像质量还有待进一步提高。
在分析现有压缩感知重构算法的基础上,本文提出一种高光谱图像变投影率分块压缩感知结合谱间双向预测稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)重构方案。实验结果表明,本文算法充分利用了高光谱图像的空谱特性,显著提高了图像的重构质量。
2 压缩感知基本原理
设x∈N是长度为N的一维信号,其稀疏表示形式为
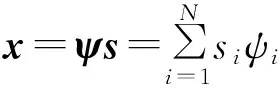
(1)

稀疏表示信号的测量过程如下:
y=Φx=Φψθ=Θθ。
(2)
式中:y是经过随机测量获得的M×1维列向量;Φ为M×N的非相干线性测量矩阵;ψ为N×N的稀疏分解矩阵;Θ=Φψ是M×N的矩阵,称为传感矩阵;θ为信号x的稀疏表示形式。
由于测量值y的维数M远远小于信号x的长度N,因此无法直接由测量值y求解原信号x。而当信号x是稀疏的,则可通过求解最优l0范数或者转化为l1范数问题来精确重构稀疏信号θ,再由θ进行稀疏基逆变换即可得到原始信号x,但整个算法复杂度过高,难以实现。
SAMP算法是匹配追踪类算法[9]中性能最好的一种,重构精度高,复杂度相对较低,且不需要已知信号的稀疏度,更适用于实际情况。同时,可以在重构框架中加入维纳滤波来清除分块压缩感知导致的重构图像方块效应。上述方法使得恢复的图像具备空间光滑特性,充分利用了图像的空间相关性。
3 高光谱图像分块测量结合优化谱间预测重构方案
高光谱图像包含丰富的光谱信息,如果对其压缩时未能充分考虑图像的特性,将会大大降低压缩性能。本文针对高光谱图像的空谱特性,提出了一种基于变投影率分块压缩感知以及优化谱间预测SAMP重构的高光谱图像压缩算法(Block-Band Pursuit-CS,BCS-BP-SAMP),图1为本文算法框图。首先利用聚类算法将高光谱图像所有频段分成参考频段和普通频段,对所有频段单独进行分块压缩感知投影,其中参考频段的投影率远高于普通频段。在重构过程中,参考频段直接利用SAMP算法重构,而对于普通频段的重构则设计了一种新模型:首先通过重构的参考频段进行双向预测,然后计算预测前后投影值的残差,最后利用SAMP算法重构该残差,以此修正预测值。迭代上述过程能够大大提高普通频段的重构精度。

图1 BCS-BP-SAMP算法框图
Fig.1 Block diagram of BCS-BP-SAMP algorithm
3.1 频段聚类算法
高光谱图像Jasper Ridge的谱间相关系数矩阵如图2所示,其中白色代表1,黑色代表0,亮度越高,表示相关性越强。

图2 Jasper Ridge相关系数矩阵
Fig.2 Correlation matrix of Jasper Ridge
由图2可知,高光谱图像相关系数矩阵有明显的分块效应。因此,想要充分利用高光谱图像的谱间相关性,必须先对高光谱图像所有频段进行聚类分组,同组高光谱图像具有非常相似的光谱特征,每一类的中心即为参考频段,其余为普通频段。传统聚类一般采用K均值(K-means)算法[10],但其聚类结果具有很大随机性,且精度较差,无法精准地确定高光谱图像中的参考频段,不利于后续压缩算法性能的提高。
本文采用近邻传播(Affinity Propagation,AP)聚类[11]对频段进行聚类分组,其基本思想是以数据点之间的相似度进行聚类,初始时将所有数据点视为潜在的类中心,通过一个迭代过程将所有数据点划分到确定的类。相比传统聚类算法,AP聚类算法速度快、精度高,非常适用于高光谱图像频段聚类分组。
3.2 分块压缩感知
相较于对高光谱图像进行整体压缩感知测量,分块压缩感知测量主要有两个优点:一是测量矩阵规模较小,便于数据存储以及硬件实现;二是数据测量与传输可同步进行,不必等到整个图像都测量完成再传送数据。但分块处理的方式容易导致重构图像出现方块效应,因此引入维纳滤波解决这一问题。
在对高光谱图像的块压缩感知的过程中,xi,j表示第i频段组中的第j个频段,将各频段图像分成B×B大小的块,xi,j,[l]为xi,j中的第l块,对每个块采用相同的测量矩阵ΦB进行测量,得到观测值yi,j,[l]=ΦBxi,j,[l],其中ΦB为MB×B2的正交独立同高斯分布矩阵,MB为图像块的观测数目,则投影率为R=MB/B2。对于参考频段和普通频段,由于测量精度不同,MB的取值也不同。整个频段图像xi,j的测量值即为yi,j=Φxi,j=Φψθ,ψ为稀疏基,θ为信号稀疏表示系数,测量矩阵Φ是如下的块对角矩阵:
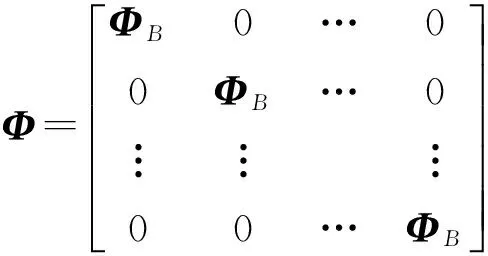
(3)
3.3 基于SAMP的参考频段重构
对于参考频段图像,直接采用SAMP算法[12]重构即可,最后利用维纳滤波来平滑整个频段图像,具体算法流程如下:
输入参数:M×N的传感矩阵A=Φψ;M×1维观测向量y;步长S。
以下流程中,rt表示残差,t表示迭代次数,Λt表示t次迭代的索引(列序号)集合(元素个数为L,L等于整数倍步长S),aj表示矩阵A的第j列,At={aj}(for allj∈Ck)表示按索引集合Ck选出的矩阵A的列集合(设列数为Lt),θt为Lt×1的列向量。
(1)初始化r0=y,Λ0=∅,L=S,t=1;
(2)计算u=abs[ATrt-1](即计算〈rt-1,aj〉,1≤j≤N),选择u中L个最大值,将这些值对应A的列序号j构成集合Sk(列序号集合);
(3)令CK=Λt-1∪Sk,At={aj};
(4)求出y=Atθt的最小二乘解,
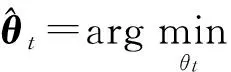
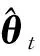
(7)如果残差rnew=0,则停止迭代进入第8步;如果‖rnew‖2≥‖rt-1‖2,更新步长L=L+S,返回第2步继续迭代;前面两个条件不满足,则Λt=F,rt=rnew,t=t+1,如果t≤M,则停止迭代进入第8步,否则返回第2步继续迭代;

3.4 基于谱间优化预测以及SAMP的普通频段重构
由于普通频段图像采样率很低,如果直接利用SAMP算法对其重构,未能充分利用高光谱图像的强谱间相关性,则重构效果很差。本文提出的基于谱间优化预测以及SAMP的普通频段重构主要过程为:通过重构的参考频段双向预测普通频段,并对其进行压缩投影,然后计算预测前后普通频段投影值的残差,利用SAMP算法重构残差来修正预测值,通过迭代过程不断修正预测值来逼近普通频段图像的原始值。
(1)普通频段预测
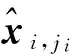


(2)计算测量值残差
采用与同一普通频段观测时所用的测量矩阵Φ对预测值进行分块压缩感知,得到对应的测量值y′i,p=Φx′i,p,则两个测量值的残差为
yr=yi,p-y′i,p=Φ(xi,p-x′i,p)=Φxr。
(4)
式中:xr为普通频段的原始值xi,p与其预测值x′i,p之间的残差,对应的测量值即为yr。
(3)残差重构
采用SAMP算法重构测量值残差yr,即可恢复普通频段原始值与其预测值之间本身的残差xr。在压缩感知重构过程中,信号的稀疏性对其重构性能有非常大的影响,信号越稀疏,则重构性能越好。利用高光谱图像的强谱间相关性对普通频段进行谱间双向预测后,预测值x′i,p非常接近原始值xi,p,则得到的残差xr比原始值xi,p更加稀疏,故利用SAMP算法重构残差比由yi,p直接重构xi,p更有效。
(4)修正预测值
通过迭代执行上述计算测量值残差、残差重构以及修正预测值的过程,使预测值不断逼近原始值。当更新的预测值基本不变时,结束迭代过程,最终得到普通频段的重构值。
4 仿真实验结果与分析
本文实验数据采用美国喷气推进实验室的AVIRIS高光谱图像Lunar Lake和Jasper Ridge,它们已经被广泛地应用于科学研究,研究结果更具可比性。为了计算简便,实验只截取了其中第一场景中的第1~256行、第1~256列的全部光谱频段,大小为256 pixel×256 pixel×224 pixel的图像块作为实验数据。实验中分块压缩感知的分块大小为16 pixel×16 pixel,频段组的数目为16,定义了投影率(测量精度)为M/N,M为观测数目,N为信号长度,其值相当于压缩比,越大表示压缩比越小,反之则表示压缩比越大。
实验运行的硬件环境为:处理器Intel Core i3(3.3 GHz)、内存2 GB的PC机;软件环境为:Windows 7操作系统,使用软件MATLAB R2013a进行实验。
图3和图4比较了本文算法(BCS-BP-SAMP)与对高光谱图像分块压缩感知后直接对各频段单独采用SAMP算法(BCS-SAMP)、文献[6]提出的利用谱间特性的高光谱图像变采样率重构算法以及各种直接利用匹配追踪类算法重构高光谱图像等同类方法的平均信噪比(Signal-to-Noise Ratio,SNR)。由图3和图4可知,对于不同高光谱图像,本文算法得到的信噪比均高于其他几种对比算法,比其中性能较优的文献[6]算法平均提高约2 dB,这是由于文献[6]算法只是进行简单的变采样率压缩感知以及单谱间预测重构,未能充分利用图像的空谱特性。而本文算法首先采用AP聚类较为精准地确定了参考频段和普通频段,然后对参考频段以远高于普通频段的投影率进行分块压缩感知,通过重构的参考频段进行谱间双向预测同时结合SAMP算法得到重构的普通频段,使得在平均投影率较低的情况下,无论对于参考频段还是普通频段都具有很好的重构效果,充分利用了高光谱图像的空谱特性,显著改善了整体的压缩性能。

图3 Lunar采用同类算法的信噪比性能对比
Fig.3 Comparison of SNR performance of Lunar for similar algorithms
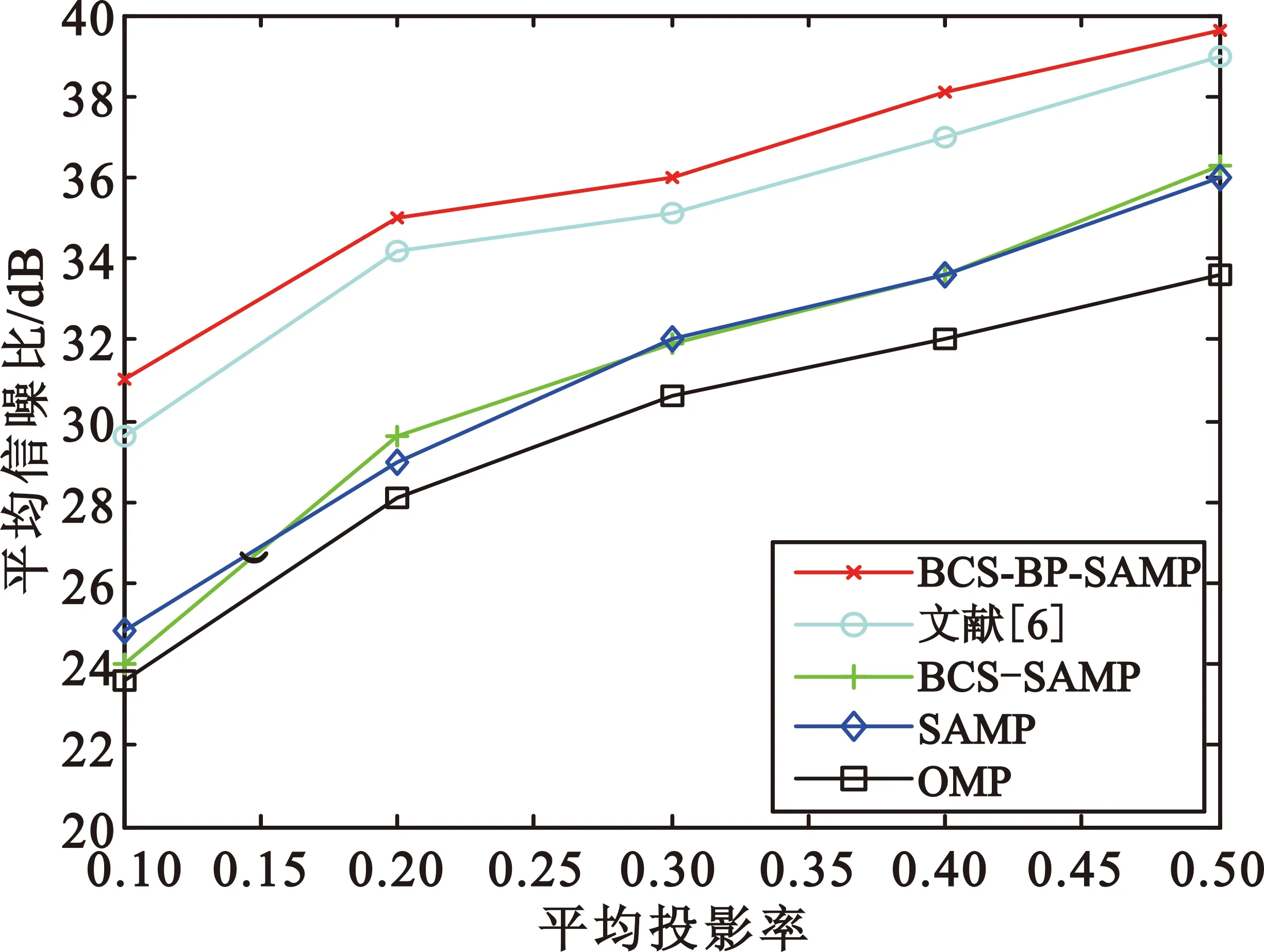
图4 Jasper采用同类算法的信噪比性能对比
Fig.4 Comparison of SNR performance of Jasper for similar algorithms
文献[7]提出的MT-Bayes压缩感知算法是一种性能优良的基于多目标的压缩感知重构方法,而文献[8]提出的KSVD-OMP算法是一种经典的基于字典学习的压缩感知重构方法,该方法能够很好地稀疏表示信号。图5和图6比较了本文算法与MT-Bayes压缩感知方法(选用了两种不同的稀疏基,DCT基和D4基)以及K-SVD-OMP算法的平均信噪比。从图中可以看出,本文算法的压缩性能依然优于对比算法,这是由于本文算法在充分考虑高光谱图像特性的情况下结合了性能较优的重构算法。
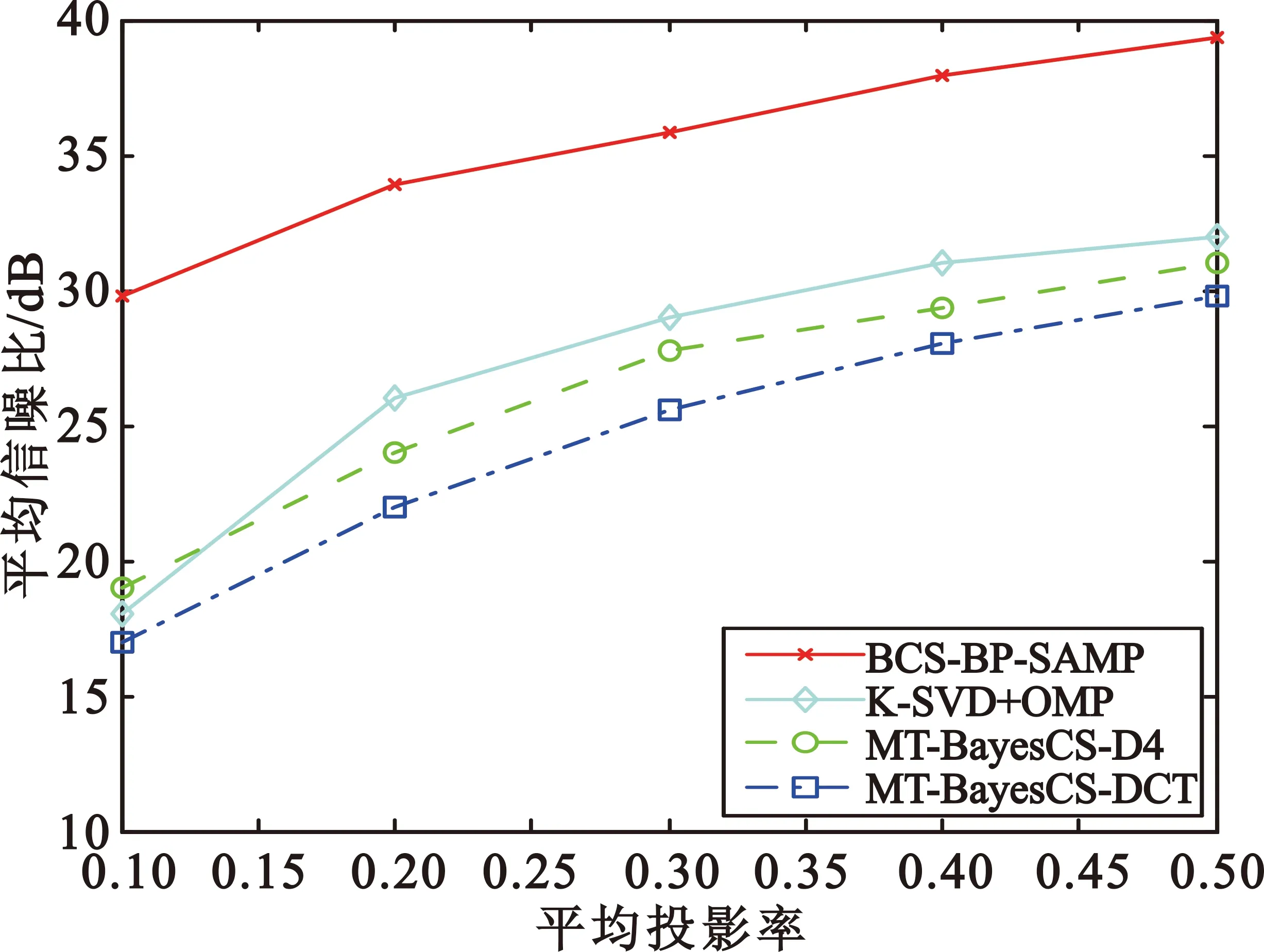
图5 Lunar采用不同算法的信噪比性能对比
Fig.5 Comparison of SNR performance of Lunar for different algorithms

图6 Jasper采用不同算法的信噪比性能对比
Fig.6 Comparison of SNR performance of Jasper for different algorithms
高光谱图像所包含的丰富光谱信息与其后续应用密切相关,对光谱信息的保真程度是衡量高光谱数据有损压缩性能的重要指标。本文采用最大谱向相似度(Max Similarity of Spectrum,MSS)[13]来反映高光谱数据的失真情况,其值越大,表示重构图像与原图像之间的光谱信息差别越大,即失真越大。由表1可知,对于高光谱图像Lunar Lake,本文算法得到的MSS低于对比算法,比性能较优的文献[6]算法平均低8左右,说明其重构图像对光谱信息的保存更完整,从另一方面证明了本文算法的有效性。
表1 各种算法的最大谱向相似度对比
Tab.1 Comparison of MSS for various algorithms

投影率最大谱向相似度MT-BCSK-SVD+OMPBCS-SAMP文献[6]BCS-BP-SAMP0.146.1640.9135.9620.1610.060.233.9133.8631.8317.097.680.326.9025.3624.6112.365.160.419.1619.2312.0610.694.390.510.369.188.867.813.66
平均投影率为0.2时,利用不同方法得到的Lunar Lake和Jasper Ridge第96频段(普通频段)重构图像的视觉效果如图7所示。当投影率很低时,采用本文算法得到重构图像比较清晰,并且在地物轮廓以及细节信息方面保存较好,在视觉效果上与原图差别不大;采用性能较优的文献[6]算法得到的重构图像总体上比较清晰,只是某些细节方面效果不够好;而采用K-SVD+OMP算法得到的重构图像非常模糊,失真较大;其他算法得到的重构图像相比本文算法在视觉效果上也不够理想。
图7 不同图像采用不同算法得到的重构图像视觉效果对比
Fig.7 Comparison of reconstructed image visual effect for different images by different algorithms
5 结束语
针对现有基于压缩感知理论的高光谱图像压缩算法对图像的空谱特性利用不够充分,导致重构图像质量偏低的问题,本文提出了一种高光谱图像变投影率分块压缩感知结合优化谱间预测重构算法。该算法充分利用了高光谱图像的空谱特性以及数据稀疏性等先验信息,同时结合了性能较优的SAMP重构算法,更加精确地重构了原始数据。实验结果表明,与同类和某些传统算法相比,本文算法显著提高了重构图像质量,改善了整体的压缩性能,具有一定的实用价值。然而,如何结合传统模式的编码压缩算法来进一步提升压缩效率,是一个值得研究的方向。
[1] DONOHO D L.Compressed sensing[J].IEEE Transaction on Information Theory,2006,52(4):1289-1306.
[2] 石光明,刘丹华,高大华,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081. SHI Guangming,LIU Danhua,GAO Dahua,et al.Advances in theory and application of compressed sensing[J].Acta Electronica Sincia,2009,37(5):1070-1081.(in Chinese)
[3] LIU H Y,LI Y S,XIAO S,et al.Distributed compressive hyperspectral image sensing[C]//Proceedings of Sixth International Conference on Intelligent Information Hidding and Multimedia Signal Processing(IIH-MSP).Darmstadt,Germany:IEEE,2010:607-610.
[4] FOWLER J E,DU Q.Reconstructions from random projections of hyperspectral imagery with spectral and spatial partitioning[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing,2013,6(2):466-472.
[5] SHU X B,AHUJA N.Imaging via three-dimensional compressive sampling(3DCS)[C]//Proceedings of 2011 IEEE International Conference on Computer Vision(ICCV).Barcelona:IEEE,2011:439-446.
[6] 赵阳.基于字典学习及压缩感知的高光谱图像重构算法研究[D].秦皇岛:燕山大学,2013. ZHAO Yang.Study on reconstruction of hyperspectral images based on dictionary learning and compressed sensing[D].Qinhuangdao:Yanshan University,2013.(in Chinese)
[7] JI S,DUNSON D,CARIN L.Multitask compressive sensing[J].IEEE Transaction on Signal Processing,2009,57(1):92-106.
[8] TROPP J,GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.
[9] 马春晖.压缩感知重构算法研究[D].杭州:杭州电子科技大学,2012. MA Chunhui.Study on the compressed sensing reconstruction algorithms[D].Hangzhou:Hangzhou Dianzi University,2012.(in Chinese)
[10] SULAIMAN S N,MAT ISAN A.Adaptive fuzzy-K-means clustering algorithm for image segmentation[J].IEEE Transactions on Consumer Electronics,2010,56(4):2661-2668.
[11] 梁玮,曾平,张华,等.基于聚类和小波变换的多光谱图像压缩算法[J].光谱学与光谱分析,2013,33(10):2740-2744. LIANG Wei,ZENG Ping,ZHANG Hua,et al.Multispectral image compression algorithm based on clustering and wavelet transform[J].Spectroscopy and Spectral Analysis,2013,33(10):2740-2744.(in Chinese)
[12] WU H L,WANG S.Adaptive sparsity matching pursuit algorithm for sparse reconstruction[J].IEEE Signal Processing Letters,2012,19(8):471-474.
[13] CHRISTOPHE E,LEGER D,MAILHES C.Quality criteria benchmark for hyperspectral imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(9):2013-2114.

陈善学(1966—),男,安徽合肥人,2009年于电子科技大学获博士学位,现为教授,主要研究方向为图像处理、信号压缩;
CHEN Shanxue was born in Hefei,Anhui Province,in 1966.He received the Ph.D. degree from University of Electronic Science and Technology of China in 2009.He is now a professor.His research concerns image processing and signal compression.
胡 灿(1989—),男,重庆人,硕士研究生,主要研究方向为高光谱图像处理;
HU Can was born in Chongqing,in 1989.He is now a graduate student.His research concerns hyperspectral image processing.
Email:563357126@qq.com
屈龙瑶(1991—),男,湖北荆门人,硕士研究生,主要研究方向为高光谱图像处理。
QU Longyao was born in Jinmen,Hubei Province,in 1991.He is now a graduate student.His research concerns hyperspectral image processing.
Hyperspectral Image Compressed Sensing Reconstruction Based on Spatial-spectral Characteristics
CHEN Shanxue,HU Can,QU Longyao
(Chongqing Key Laboratory of Mobile Communications Technology,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)
The existing hyperspectral image compressed sensing reconstruction algorithm can not fully utilize the spatial-spectral characteristic of image so that the quality of the reconstructed image is not high enough.For this problem,a new compression scheme for hyperspectral images is proposed which is based on variable projection rate sub block compressive sensing and reconstruction of optimized inter spectral prediction.At the encoder,all bands of the hyperspectral image is divided into some reference bands and common bands by band clustering,different bands are used to separate the compressed sensing with different precision in order to obtain hyperspectral data.At the decoder,the reference band is reconstructed by using sparsity adaptive matching pursuit(SAMP) algorithm,and for reconstruction of the common band,a new model of optimized inter spectral prediction combined with SAMP algorithm is designed:firstly,the common band is predicted by means of the reconstructed reference band,and it is compressed and projected,then the residual error of the projection value of prediction before and after is calculated for the common band,finally,the SAMP algorithm is used to reconstruct the residual error,which is used to correct the prediction value.Experimental results show that compared with similar algorithms,the proposed algorithm fully considers the spatial-spectral characteristics of hyperspectral images,effectively improves the quality of reconstructed image,and the complexity of encoding is low,and the hardware implementation is easy.
hyperspectral image;block compressed sensing;band clustering;optimized inter spectral prediction;sparsity adaptive matching pursuit
10.3969/j.issn.1001-893x.2016.07.001
陈善学,胡灿,屈龙瑶.基于空谱特性的高光谱图像压缩感知重构[J].电讯技术,2016,56(7):717-723.[CHEN Shanxue,HU Can,QU Longyao.Hyperspectral image compressed sensing reconstruction based on spatial-spectral characteristics[J].Telecommunication Engineering,2016,56(7):717-723.]
2016-01-29;
2016-04-25 Received date:2016-01-29;Revised date:2016-04-25
国家自然科学基金青年科学基金资助项目(61302106);河北省自然科学基金资助项目(F2014502029);中央高校基本科研业务费专项资金资助项目(2014MS100)
Foundation Item:The Young Scientists Fund of the National Natural Science Foundation of China(No.61302106);The Natural Science Foundation of Hebei Province(F2014502029);Fundamental Research Funds for the Central Universities(2014MS100)
TN911.73;TP751.1
A
1001-893X(2016)07-0717-07
**通信作者:563357126@qq.com Corresponding author:563357126@qq.com

