基于ARIMA模型的短期股票价格预测

吴玉霞，温 欣

（1.河北金融学院 河北省科技金融重点实验室，河北 保定 071051；2.财政部财政科学研究所博士后流动站，北京 100142；3.南京财经大学 经济学院，南京 210023）

基于ARIMA模型的短期股票价格预测

吴玉霞1,2，温 欣3

（1.河北金融学院 河北省科技金融重点实验室，河北 保定 071051；2.财政部财政科学研究所博士后流动站，北京 100142；3.南京财经大学 经济学院，南京 210023）

文章选取“华泰证券”250期的股票收盘价作为时间序列实证分析数据，通过建立ARIMA模型对创业板市场股票价格变动的规律和趋势进行了预测。实证结果表明，该模型短期动态、静态预测效果较好，可以为投资者和企业在进行相关决策时提供有益参考。

时间序列分析；股票价格预测；创业板；ARIMA模型

0 引言

创业板股价较主板股价波动幅度更大，预测难度也更大。时间序列预测方法是比较常用的预测方法，它有一系列完善的理论基础，随着人们对股市的追捧，不少学者也尝试将时间序列预测应用于股票的价格预测，具体的讲时间序列预测股价是将股票价格或者价格指数看作变化的时间序列，通过建立合理的时间序列模型以预测未来发展变化的规律和趋势。但目前对股票价格的预测更多地是对主板市场的研究，鲜有对创业板市场股票价格的预测。本文选取“华泰证券”250期的股票收盘价作为时间序列实证分析数据，通过建立ARIMA模型对创业板市场股票价格变动的规律和趋势进行预测。需要指出的是，股票市场的行情是千变万化的，时间序列分析法只是利用历史数据，期望从中获取有用信息来预测将来走势，而并没有考虑影响股价变动的原因，故一般只是直观分析，仅做短时间内的预测。

1 股票价格预测理论与方法

1.1 股票价格预测理论

股票价格序列预测就是利用事物发展的历史数据，综合考虑各种影响股价的因素，采用某种科学的方法，对将来某一期或者某几期的股票价格进行估计，已知时间序列{Y1,Y2,…， }

YT，预测YT+1，···，YT+m的股票价格，公式定义为：

其中，只进行一步预测，即仅求YT+1称为单步预测，当预测YT+m，m＞1，称m步预测。显然m步预测可以拆分成多个单步预测的组合，即式（1）可以写成：

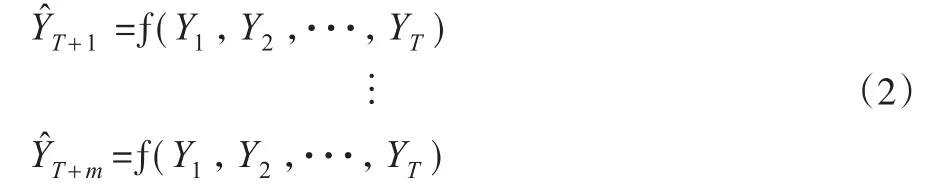
预测研究的是未来的状态或发展趋势，它之所以受到广泛关注是因为人们现在的行为可能影响到未来的结果，将各种预测方法应用于股票价格预测，给本文投资决策提供建议，可能会关系到以后的股票投资收益，因此股价预测是非常现实的预测问题。

1.2 时间序列分析法

时间序列预测方法是将股票价格或者价格指数看作变化的时间序列，通过建立合理的时间序列模型以预测未来发展变化的规律和趋势，而时间预测方法正迎合股指的变化发展的随机性及其时变性等特点，有较好的短期预测效果。常用的时间序列分析法有自回归模型(AR)、移动平均模型(MA)及自回归移动(ARMA)平均模型等。预测方法又有两种：一种是动态预测：只能进行一期预测，在由实际值预测出第一期的值之后，将第一期预测值带入时间序列，和历史数据一期再进行第二期的预测，以此递推，对于长期预测，可能会产生累计误差；另一种是静态预测：用原序列的实际值来进行预测，只有当真实数据可以获得时才可以使用这种方法。

2 ARIMA模型的实证分析——基于创业板市场数据

2.1 模型介绍

C.P.Box和G M.Jenkins[1]最早提出的自回归求和移动平均模型（简称为ARIMA模型)，是将非平稳时间序列先经过d阶差分平稳化，再对得到的平稳时间序列利用自回归(AR(p)process)和滑动平均过程(MA(q)process)，并通过样本自相关系数(ACF)和偏自相关系数(PCF)等数据对建立的模型进行辨识，同时还提出了一整套的建模、估计、检验和控制方法。设{} Yt为零均值的平稳时间序列，p阶自回归q阶滑动平均的ARMA（p，q）公式表述为：

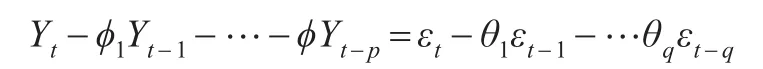
可简写为ϕ(B)Yt=θ(B)εt。ARIMA（p，d，q）模型中的d是差分阶数，金融市场上的时间序列数据一般都是非平稳的，差分是平稳化的途径之一，差分后的ARIMA建模过程基本与ARMA相同。

2.2 模型的建立

在数据选取方面，随机选取个股。华泰证券股票发行以来，股票价格没有明显的异常波动，选取的250期时间序列内无重大财务、违法违规事件。之所以选250期是因为若选取数据过少则无法充分提取历史数据中的信息，数据选取过多又会因间隔较长时的股价会对后期的预测股价影响较小造成不必要的误差。本文最终选取华泰证券2014年3月24日至2015年3月31日间250期的股票的收盘价作为时间序列数据，（数据来源于大智慧和同花顺历史股价）。剔除7个无效数据，对243期股票的收盘价做ARIMA模型拟合，并进行短期预测。命名收盘价时间序列为y,对y进行ADF平稳性检验，发现y序列非平稳。接下来要进行平稳化处理，对其进行差分，直至平稳。一阶差分结果如下：

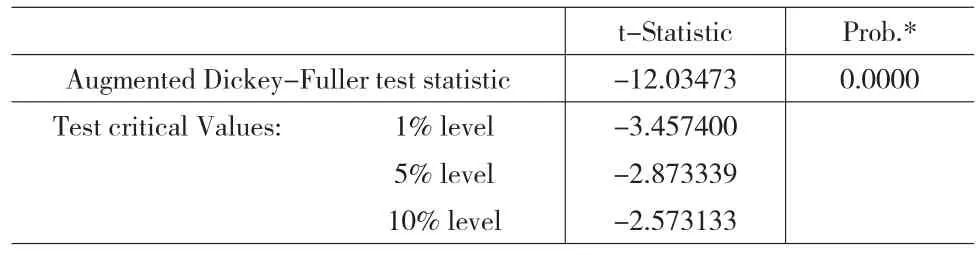
表1 一阶差分序列ADF检验

可以看出dy的ADF统计值的绝对值为12.03473，大于显著性水平为0.05时的2.873339，故接受存在一个单位根的原假设，并且P值很小，均说明一阶差分序列是平稳的，因此d=1。

图1 一阶差分的时序图

图2 一阶差分自相关图

dy的时序图围绕一个常数值上下波动，且波动范围不大。自相关图中自相关系数迅速衰减为零，也表明一阶差分序列是平稳的，不需再进行二阶差分检验。

由图1序列相关图可知，P值都小于5%，数据为非白噪声序列，存在相关性，有一定规律可循。偏自相关系数在k=1后很快趋于0，偏自相关1阶截尾，可以试着拟合AR（1）模型，在k=3时在2倍标准差的置信带边缘，可尝试AR（3）模型；自相关系数在k=1时显著不为零，在k=3、6处在2倍标准差的置信带的边缘，是可以尝试拟合MA（1）、MA（3）、MA（6）模型；同时可以建立ARIMA（1，1，1），ARIMA（3，1，1）模型等。由模型定阶发现，p可能等于1、3、6，q可能等于1，表2、表3分别是各模型的估计结果和预测的参数对比表。

表2 方程的P值比较

比较表2中的P值，综合c、ar(p)、ma(q)三项的P值，发现模型ARIMA（3，1，1）的最小，都小于显著性水平5%。

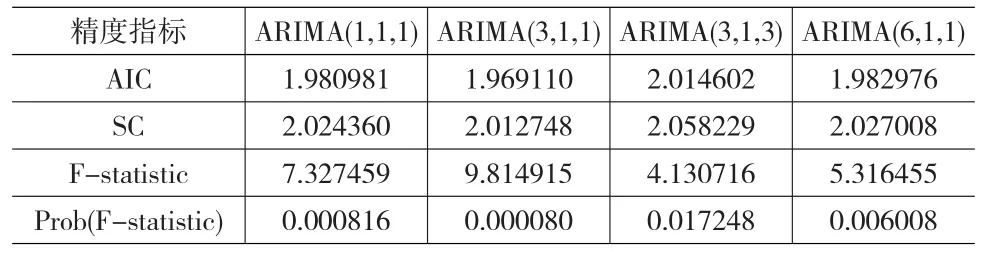
表3 各种模型的精度指标对比

比较各模型的检验统计量，根据AIC准则、SC小的为较优模型，也是ARIMA（3，1，1）比较好，优于其他三个模型。F统计量9.814915在四项中最大，P值也最小。综上拟选定ARIMA（3，1，1）模型。

较优的模型ARIMA（3,1,1）用公式表述为：

2.3 模型的诊断检验

在确定参数的估计值后，还需要对拟合模型的适应性进行诊断检验。本文利用Eviews软件建立残差的自相关图，对残差进行纯随机性检验，ARIMA（3,1,1）的残差自相关检验结果如图3所示。

图3 ARMA（3，1，1）模型残差相关图

残差相关图显示自相关函数基本在95%的置信区域内，且P值大于0.05，残差为白噪声，也即残差是纯随机性的，图4 ARIMA（3，1,1）模型拟合图也显示拟合模型有效。

图4 ARMA（3，1，1）模型拟合图

2.4 模型的应用

用拟合的有效模型ARIMA（3，1,1）进行短期预测。首先进行动态预测，预测图如下：

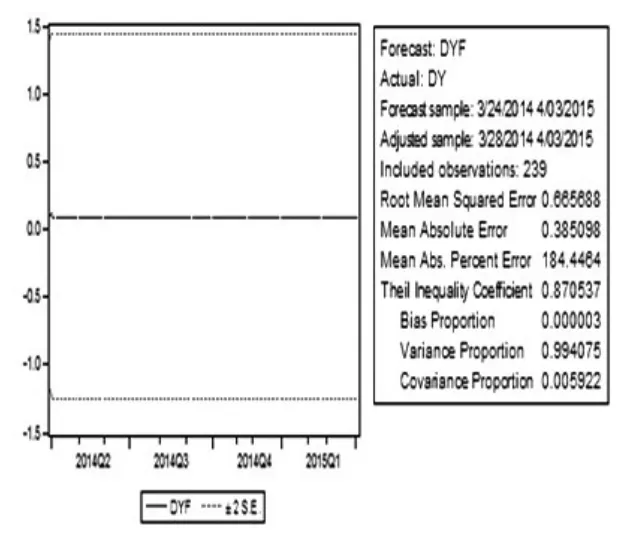
图5 序列动态预测图

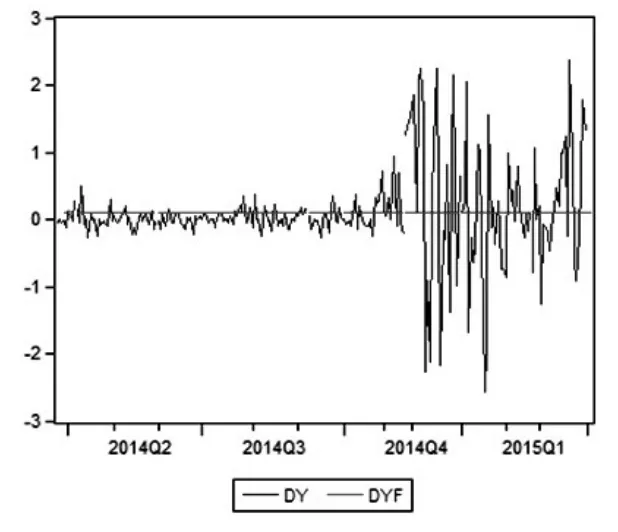
图6 动态预测效果图

预测值存放在DYF序列中，作出dy和dyf动态关系图。如图6，动态预测值几乎是一条直线，说明动态预测效果不好。

再进行静态预测，静态预测只能进行向前一步预测，预测结果见图8，可以看出静态预测效果还是很理想的。

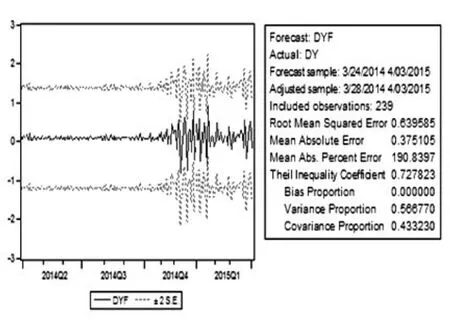
图7 静态预测图

图8 动态预测效果图

根据存放在dyf中的预测值，利用公式反推第一期预测值，将预测值加入历史时间序列，同样的过程可得出第二期预测值及直到m期。由于模型的局限性，这里只给出三期真实值与预测值的比较情况，结果如表4所示。

表4 ARIMA（3,1,1）模型预测结果

从预测拟合图可以看出，该模型的预测效果较好，绝对误差还是比较小的，相对误差只有0.0135，从预测结果分析不难得出以下结论：

第一，ARIMA模型作为华泰证券指数的短期预测模型是可行的，从拟合图可以看出拟合效果较好，说明此时间序列包含了华泰证券股价指数的大部分信息，并且可以看出静态预测效果好于动态预测。比如，华泰证券2015年3月31日的股价为30.11，之前几期的股价以次为28.79、27、26.46、26.71，预测的结果分别为30.34、30.17、30.08，明显股价有增长趋势，这时可以考虑买进，以期获利。

第二，模型倒推去计算预测值很可能产生累计误差，从表4 ARIMA（3,1,1）结果图中就可以看出，向前一期预测的误差值是0.28，向前两期是-0.18，向前三期绝对值大于前两期的误差为2.53，因为二期的预测值是由一期预测值推算的而非通过一期的真实值计算，这一特点不利于长期预测，但从相对误差及平均相对误差看，这三期的误差还是很小的，预测效果还是比较理想的。

第三，时间序列本身的特性就是从历史数据中提取有用信息，来对未来走势进行预测，影响股价的其他因素仅以随机项来反映，这也是时间序列模型的一个缺陷，本文不能对其他影响股价的因素进行控制，在进行数据选择的时候，还要尽量避免受政策等影响产生重大波动的情况，以降低预测误差。

3 结论

股票价格预测是一个充满挑战性的问题，但时间序列预测理论一直被认为是对股价变化进行统计预测的有效手段。因为时间序列预测理论具有很好的短期预测效果，虽然本文仅用了一步静态预测的方法，但理论上时间序列可实现动态的连续预测，本文的实证分析也表明ARIMA模型作为华泰证券指数的短期预测模型是可行的，此时间序列包含了华泰证券股价指数的大部分信息，且拟合效果较好，从而ARIMA模型的应用对本文把握住创业板买卖时机及回避风险也有一定参考价值。

由于时间有限，本文只针对华泰证券部分收盘价价格指数实际数据的变化做了建模分析，并且当样本数据发生变化时，模型的参数结构会随之变化，这表明模型对样本的变化十分敏感，对股价预测的波动模式有短期稳定性，预测的精度也因样本变化而变化，结论可能缺乏普遍性，这就要求在利用ARIMA模型进行股价预测时，对发展比较稳定，无因突发事件、政策出台等外界因素产生较大异常波动的历史数据效果更好。

总之，本文通过建立时间序列模型，利用历史价格作为序列数据，对未来几期价格进行短期的预测，希望能够帮助投资者降低投资风险和发现投资机会。同时可以考虑结合其他预测方法，加强对股票市场自身体制因素、国家宏观经济政策、国民经济发展方向等各种因素的关注，常常这些不定因素对股票的长期走势也有着重要的应用价值。

[1]贺本岚.股票价格预测的最优选择模型[J].统计与决策，2008,(6).

[2]曹冬.中国创业板市场发展的思考[J].理论前沿，2008,(1).

[3]李秀琴,梁满发.基于ARIMA模型的股票行情预测[J].长春教育学院学报，2013,(7).

[4]厉雨静,程宗毛.时间序列模型在股票价格预测中的应用[J].商场现代化，2011,(33).

[5]徐国祥.统计预测与决策[M].上海：上海财经大学出版社，2008.

[6]杨阳.股票价格预测方法研究[J].经营管理者，2011，(16).

[7]翟志荣，白艳萍.时间序列分析方法在股票市场中的应用[J].太原师范学院学报(自然科学版)，2011，(1).

（责任编辑/浩 天）

F830.91

A

1002-6487（2016）23-0083-04

吴玉霞（1971—），女，河北邢台人，博士后，副教授，研究方向：国民经济统计分析。温 欣（1993—），女，江苏徐州人，硕士研究生，研究方向：金融统计分析。