参数法、半参数法的动态VaR模型风险度量
张 琼,黄旭东,林雪勤
(1.安徽师范大学a.经济管理学院;b.数学计算机科学学院,安徽芜湖241000;2.国泰安教育技术股份有限公司,合肥230088)
参数法、半参数法的动态VaR模型风险度量
张 琼1a,黄旭东1b,林雪勤2
(1.安徽师范大学a.经济管理学院;b.数学计算机科学学院,安徽芜湖241000;2.国泰安教育技术股份有限公司,合肥230088)
文章采用参数法和半参数法,分别考虑标准化收益在GED、SGT、GPD分布下以及FSH方法下的GARCH模型、EGARCH模型和PGARCH模型的风险测度的准确性,据此组建了12种风险测度的动态VaR模型,并采用道琼斯股票市场指数和上证指数进行实证分析。对收益率进行基本统计分析发现两个股票市场的收益率都不服从一般的正态分布。运用后验测试的方法,对所有模型的样本外预测动态VaR值采用LR、LRuc和DQ三种方法综合检验,并由损失函数值可以看出:GARCH模型的风险度量能力最弱,在置信水平99.5%下,EGARCH模型最准确,在置信水平95%下,PGARCH模型最准确;GED分布描述市场的准确程度相对最弱,在较高的置信水平下,半参数模型能更好地度量市场的风险,在较低的置信水平下,参数模型能更好地度量股票市场的风险。
动态VaR模型;风险测度;损失函数
0 引言
做好风险管理,最重要的一个环节是进行风险度量,金融风险度量的主要手段之一是在险价值(Value at Risk, VaR)。VaR可以看作是建立在过去和现在信息上的未来投资组合的分位数,由于投资组合的收益分布随时间在变化,如何准确的估计VaR,在实践中是一个很大的挑战。估算VaR方法主要有参数法、半参数法和非参数法。
在参数法中,GARCH模型是应用最为广泛的时间序列波动率模型,然而在GARCH模型应用中,基础的研究通常假设资产收益服从正态分布,而大量的实证分析表明资产收益表现出非对称性、厚尾、尖峰等特征,因此假设服从正态分布来估计投资组合的动态VaR,对于风险管理者来说,不能产生好的预测结果,常常严重低估风险。如徐炜和黄炎龙(2008)比较研究GARCH族的11种模型分别在正态分布和Skewed-t分布下度量动态VaR值的精确程度,结果表明Skewed-t分布较好地拟合了金融资产的厚尾特性,Cheng和Hung(2011)在GARCH模型中比较了正态分布、t分布、SSD和GED下的动态VaR,结论是假设服从SSD和GED下的动态VaR得出的结论最好。Polanski和Stoja (2010)比较了正态分布、t分布、SGT和EGB2分布,发现仅后两种分布提供了精确的动态VaR估计。
半参数方法主要是将非参数和参数法结合。在非参数法中,最典型的就是历史模拟法,Trenca(2009)等结论表明单纯使用历史模拟法对于估计VaR不准确,历史模拟法常常会低估风险,并且对于一些重大事件的灵敏性比较低。Barone-Adesi等(1999)提出的一种半参数方法:FSH (Filtered Historical Simulation)方法,即将历史模拟法和条件波动率模型相结合。Marimoutou等(2009)认为FSH继承了历史模拟法优势的同时提高了模型的灵敏度。Zikovic等(2009)的研究表明FSH方法的预测效果比历史模拟法优越很多。应用极值理论方法(EVT)考虑尾部分布所具有的特征和市场极端变动有密切关系是另一种半参数方法,极值理论方法不对金融收益整体分布进行建模,仅考虑分布的尾部特质。高莹等(2008)将基于极值理论的GARCH-EVT模型与普通的GARCH-NORMAL模型进行比较,结果表明GARCH-EVT模型优于GARCH-NORMAL模型。Bekiros和Georgoutosos(2005)指出在较高置信水平下,EVT理论体系对于极端事件损失的预测最准确。
近年来,已有学者在不同置信水平下研究不同模型的准确性,如叶青(2000)引入基于GARCH模型的方差协方差法和David Li提出的半参数法对中国的股票市场进行了模拟。Chen等(2013)比较了不同置信水平下不同方法计算的VaR值的准确性。然而对于GARCH族模型下,利用参数法和半参数法在不同置信水平下对动态VaR模型的准确性进行比较的文献相对较少,且用两种不同市场的数据同时实证分析,得到的结果显然更具说服力。
因此本文基于三种有代表性的GARCH模型(GARCH、EGARCH、PGARCH)的参数与半参数动态VaR模型,考虑标准化收益在GED、GPD、SGT分布下以及FSH方法下,探究在不同置信水平下,动态VaR模型预测的灵敏度,从而找到最优预测模型,为金融市场的风险测度提供合适的度量工具。
1 动态VaR模型的定义及其估计
1.1 动态VaR模型的定义
VaR是指在给定的概率α下,在某一段时期内,预测投资组合的最大损失值,也是投资组合收益分布的特定分位数的估计,数学表达式为:
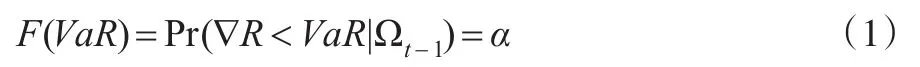
其中F(·)是投资资产组合收益的分布,∇R是某一段时期内投资组合值。VaR按是否考虑波动率的时变性,分为静态VaR和动态VaR,静态VaR是没有考虑波动率的时变性,只是由前一时间段的整体波动率来预测下一刻的波动率。而动态VaR考虑了波动率的时变和股票收益序列的波动集群性,下一刻的波动率由前一时刻的波动率来预测,有更好地准确性和及时性。
动态VaR模型的表达式为:

故在给定置信水平1-α情况下,对于式(2),主要由两部分组成,一是波动率(即条件均值和条件方差);二是θ,即标准化收益的分位数。
动态VaR模型中对于波动率GARCH模型和θ值的确定都需要知道标准化收益zt的值或者zt服从的分布,本文的研究假定zt服从GED、SGT、GPD分布,将资产收益数据进行中心化得到条件标准化收益zt,利用最大似然法估计出zt在不同分布下GARCH、EGARCH和PGARCH三个模型中的未知参数,然后又采用FSH方法对三个模型的未知参数作出估计。
1.2 动态VaR模型波动率的估计
GARCH模型是反映金融市场时变特征最常用的波动率模型,它能有效捕捉股市的丛集性效应、非对称特征等。
GARCH族模型有多种不同类型的表达形式,其中最具有代表性的是GARCH(1,1)、EGARCH和PGARCH三个模型。
Bollerslev在1986年提出的线性对称GARCH(1,1)模型,具体表达式为:
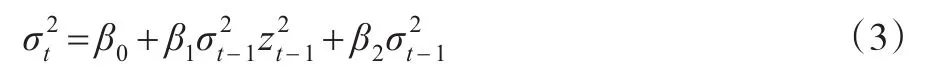
Nelson在1991年提出指数形式的GARCH模型(EGARCH模型),模型的表达式为:
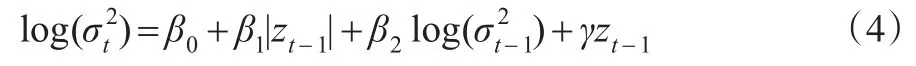
模型中条件方差采用对数形式,即使参数为负数,条件方差也是正的,这就规避了参数都为正的条件。若γ≠0时,说明信息作用非对称。
PGARCH模型是对GARCH模型作了进一步的扩展,对标准差的幂次进行模拟,这个幂并不需要事先给定,而是通过模型自身来决定。它的形式为:则模型是对称的;反之不对称。E(zt)=0,VaR(zt)=1,限制条件为 β0>0,0≤β1<1,0≤β2<1。
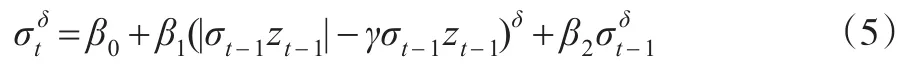
这里的μt和σt是建立在Ωt-1={rt-1,rt-2,…}上的条件均值和条件标准差
1.3 动态VaR模型θ值的估计方法
估计标准化收益zt的分位数θ,需要先知zt的整个分布或部分分布。
(1)参数法
在传统的研究中,常常假设zt服从标准正态分布,但是在实践中我们发现即使对于标准化收益的分布仍然有尖峰、厚尾等特征,需要对zt的分布作出新的假设。
GED(Generalised Error Distribution)分布是Newey在1991年提出,其密度函数的表达式为:

SGT(the Skewed Generalized T Distribution)分布是由Theodossiou在1998年提出的,标准化收益zt的SGT分布的密度函数表达为:
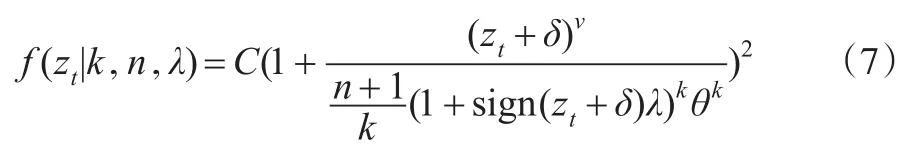
其中sign是符号函数;λ是偏度参数,且|λ|<1;正数k和n是尖峰参数,且B(·)是 Beta函数。

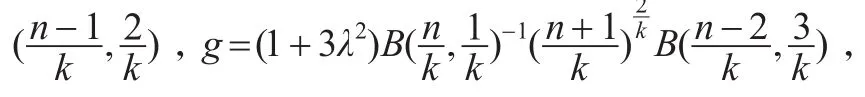
(2)半参数法
Barone-Adesi等(1999)对于标准化收益分布的刻画提出了一种半参数模型,即FSH(Filtered Historical Simulation)模型。此模型是非参数和参数方法的一种结合,利用历史模拟法来模拟标准化收益的分布,然后将历史模拟法得到的数据特征(如捕捉金融数据的厚尾、偏态等非正常特征)和GARCH模型相结合,从而估计出标准化收益的分布。
另一种半参数法是依据条件极值理论(Extreme Value Theory,EVT)进行估计。首先,定义超过阈值u分布的条件概率函数为:
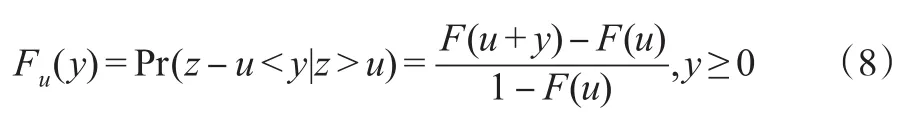
Balkerma等(1974)指出GPD(Generalised Pareto Distribution)是Fu(y)的极限分布,并且论证了当阈值u足够大时,Fu(y)=Gξ,σ(u)(y)。
这里的Gξ,σ(u)(y)表示服从GDP分布,具体表达式为:
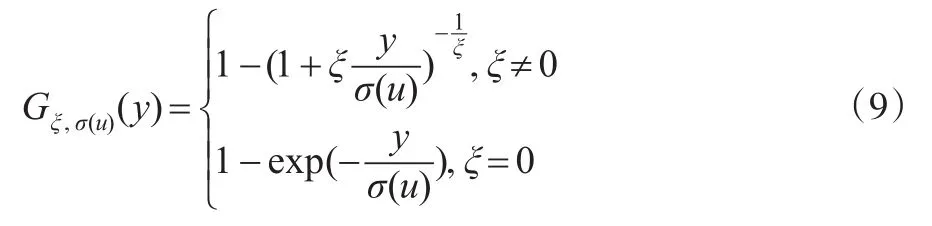
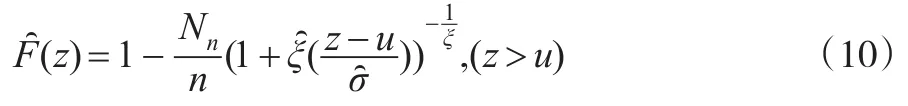
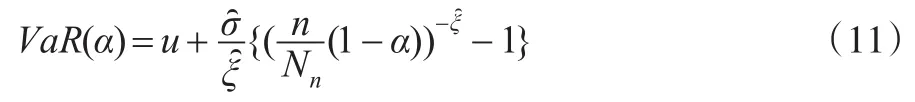
2 动态VaR模型风险测度准确性的度量
2.1 动态VaR模型的可行性检验
对于动态VaR模型预测能力的可行性检验,主要运用回测检验的方法,本文采用非条件覆盖似然比率检验(the LR of Unconditional Coverage testing)、条件覆盖似然率检验(the LR of conditional Coverage test)和条件分位数回归检验(the Dynamic Quantile test)这三个检验来综合判断,一个准确的模型均应该通过这些检验。
对于异常事件通常有如下描述,将预测第t+1天的动态 VaRt+1(α)与当日投资组合 rt+1进行比较,若rt+1<VaRt+1(α),则称异常事件出现。则定义异常指标变量如下:
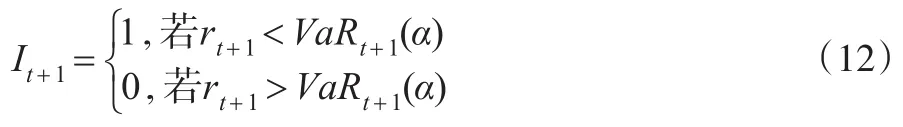
非条件覆盖似然比率检验(简记LRuc)是Kupiec(1995)建立的,这个检验是假设小于动态VaR(α)的观测值的实际个数和期望值是相等的,即原假设与备择假设分别是:似然检验统计量为:
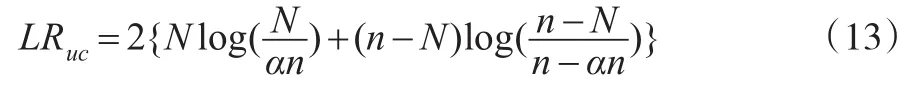
条件覆盖似然率检验(简记LRcc)是Christoffersen (1998)提出的,指出动态VaR估计可以看作是金融收益分布在较低尾部的区间预测。此检验是一种联合检验,即①是否②It+1是否独立同分布。LRcc检验的原假

其中:
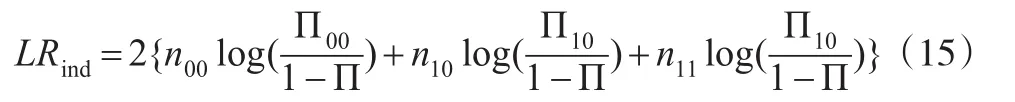
nij是It=i时It+1=j出现的个数,t=1,2,…,n-1。相应地依据此检验,可以判定当产生过多或者过少的聚类异常事件时,拒绝动态VaR模型。
自信息技术出现以后,凭借着出众的性能与能力,信息技术成功的被应用到人类社会发展的方方面面。信息技术不仅改变了人们对生活工作的看法,同时也提高了人们的生活学习质量。尤其是在教育系统当中,信息技术的出现更是有着丰富教育资源,实现教育公平,不受时间地域限制的线上教育等功能和优势。成人教育是我国教育系统中一项非常重要的教育,和全日制教育有着不同的教育形式和教学形式。是帮助成人取得专业资格、提高技术、丰富知识、增长能力的重要途径。因很多成人缺少足够的时间参与课堂学习,因此信息技术在成人教育中有着重大潜力,这就要求成人教育教师必须要掌握信息教育素质。
条件分位数回归检验(简记为DQ检验)由Engle和Manganelli(2004)提出,基本原理为当动态VaR已估计,检验异常事件指标和属于Ωt-1的所有变量是否相关。首先定义一个序列变量指标函数:

其中I(·)是示性函数,1-α是给定的置信水平。Engle和Manganelli(2004)提出一个优的模型应该产生一系列无偏性、无相关性Hit,并且Hit的期望为0,因此DQ检验同时检验两个方面内容:①E(Hitt)=0;②Hitt是互不相关的。这两个检验内容通过下列回归进行检验:

其中X=(1,Hitt-1,Hitt-2,…,Hitt-p,X1,…,Xq),B=(β0,β1,…,βp+q)T,Xj是属于Ωt-1的解释变量。检验的原假设H0∶B=0。在原假设基础上的条件分位数检验统计量为:
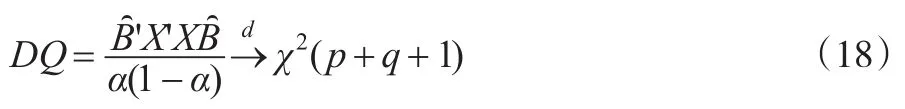
2.2 动态VaR模型风险估计准确程度的度量
对于风险管理者来说,关注的不仅仅是异常事件是否发生,更关注当异常事件发生后损失的大小,因为损失的大小和金融机构储备金多少有直接关系。Lopez(1998)提出利用损失函数作为评估异常事件发生后产生的后果,主要考察当异常事件发生时,观察值rt与预测的动态VaRt之间的距离,包含了异常事件发生的次数和损失大小。表达式为:
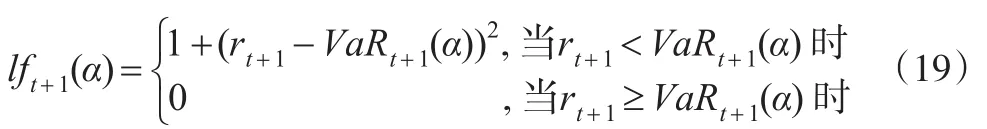
对于动态VaR模型的优劣,可通过lf的大小表现出来,所以当一个模型的lf值小于另一个,这个模型便优于后者。
3 实证分析
实证分析的数据选取了中国股票市场的上证指数和美国股票市场的道琼斯指数。
道琼斯指数选用了1991年1月2日到2013年12月30日的收盘指数(共5294个样本)作为实证分析的数据,中国的上证指数选用了2012年2月20日到2014年11月7日的每日收盘指数(共660个样本)作为实证分析的数据,所有的数据来源于国泰安数据库。
3.2 股指对数收益率的统计特征

表1 道琼斯指数(1991/1/2-2013/12/30)描述性统计
由表1可以看出,道琼斯股票指数的每日对数收益指数JB=16977.66>5.3995,JB对应的概率P=0.00<0.05,说明金融收益序列不服从正态分布。且偏度S=-0.153461<0,则说明序列分布左尾比右尾密集,峰度K=11.37894>3,,则说明此序列的分布比正态分布的峰部更尖。
作出上证综合指数的对数收益率基本统计分析的时间序列图、分布图、核密度图和Q-Q图,如图1所示。

图1上证指数对数收益率的基本统计分析图
图1 直观的展现了我国股票市场对数收益率的一些特性。由分布图和核密度估计图可以观察到我国对数收益率左偏并且有很高的峰度;Q-Q图上的点在两端处明显偏离所示直线,可见上证综合指数收益率不服从正态分布。
对两个不同的股票市场的收益率进行基本统计分析发现,两个市场的收益率都不服从一般的正态分布。
3.3 模型的参数和动态VaR值估计
对于道琼斯指数,本文选用1991—2000年的数据作为前段数据,估计出条件均值-方差模型以及标准化收益的分布函数的未知参数。然后用2001年的数据来评估模型的好坏,即假设2001年的条件均值-方差满足前10年估计出来模型,并且分布函数在2001年不变。利用2000/12/ 29(2000年交易最后一天数据)估计2001/1/2(即2001年交易第一天)条件均值-方差,再利用2001/1/2真实收益数据和条件均值-方差,预测出2001/1/3的条件均值-方差,以此类推,得到2001年每天条件均值-方差。接着利用前十年已估计概率分布得到不同模型对应的分位数θ,对伴随概率α取不同的值,在本文中伴随概率取0.5%、1%、2.5%和5%,由式(2)算得不同模型基于滚动样本上2001年每天的VaR估计值,根据式(12)异常事件的定义,统计出相应模型中异常事件的个数。再接着剔除1991年数据,加入2001年实际收益数据,同上面的做法求得2002年的动态VaR值和对应的异常值个数,同理一直滚动求解出后面的年份的动态VaR值和对应的异常值个数,直到2013年,运用每10年的滚动样本,分别产生了12个不同模型后13年评估的VaR值和异常值个数,得到3269个动态VaR值的评估数据。
对于上证指数,本文选用了2012/2/20—2013/3/14的数据作为观测样本,以前220个交易日数据作为前段数据估计出条件均值-方差模型,以及标准化收益的分布函数的未知参数。然后用接下来40个交易日的数据进行检验。同道琼斯指数的估计方法,对12种模型分别产生了440个的评估数据。
以上证指数为例,图2给出了2013/1/11—2014/7/15的上证指数的对数收益率,并给出了在置信水平99%和95%下,GARCH模型下参数(SGT)和半参数法(GDP)估计出的每日动态VaR值。
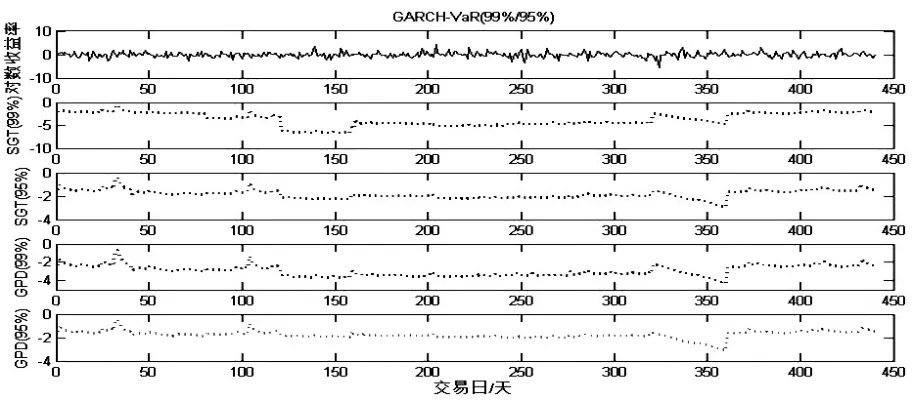
图2 不同置信水平下GARCH模型的每日动态VaR值
从图2可以看出,在不同的置信水平下,基于GARCH模型下参数(SGT)和半参数法(GDP)估计出的VaR值都刻画出了金融行业的市场风险,随当前波动性产生了很明显的变化。
3.4 模型的检验和准确程度的度量
在不同的置信水平下,采用LR、LRuc和DQ三种检验方法综合判断各个动态VaR模型的准确性是否达到既定的水平,并根据式(19)求得各个模型的最大损失函数值lf,评估出这些动态VaR模型准确程度的优劣。
在不同置信水平下,12种模型对于道琼斯指数和上证指数的检验结果在表2至表4中,各表中第一列是波动率模型,第二列是标准化收益的分布,Lruc表示对应模型给定样本的Lruc检验值,Lrind表示对应模型给定样本的Lrind检验值,DQ表示对应模型给定样本的DQ检验值,lf表示给定样本各个模型的最大损失函数值,排序指的是最大损失函数值对应的排列顺序,没有全部通过三种检验的模型不参与排序。
表2给出了置信水平99.5%下的动态VaR模型检验。当伴随概率α=0.5%时,Lruc检验、Lrind检验和DQ检验对应的拒绝零假设的边界值分别为
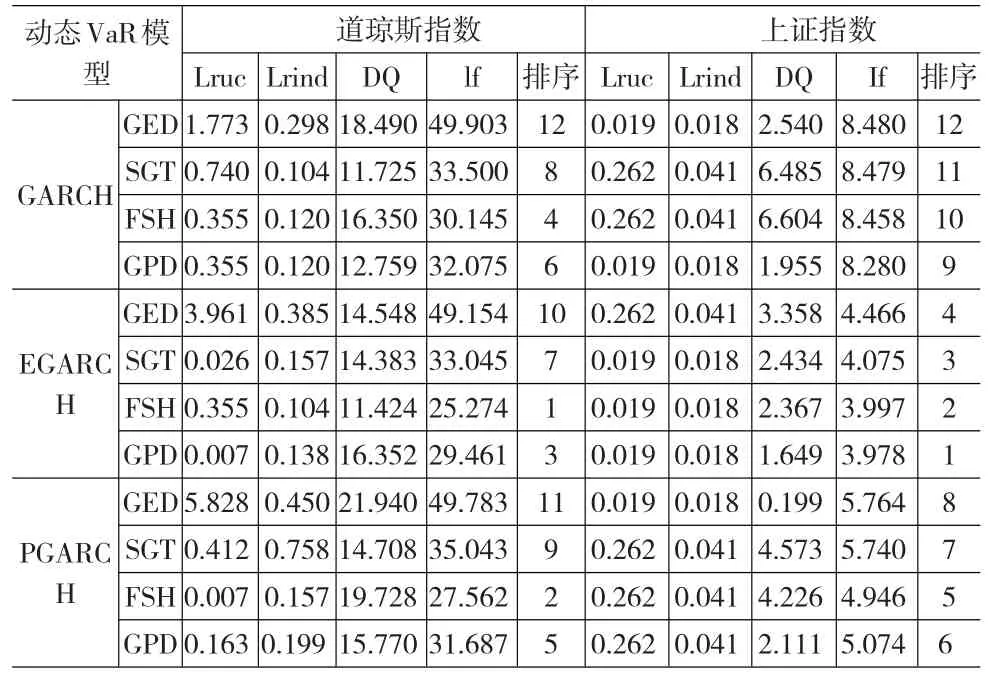
表2 置信水平99.5%下的动态VaR模型检验
由表2可知,在置信水平为99.5%下,12种模型均通过第一阶段的三种检验,即12种模型预测的准确性都可以接受。由损失函数lf的估计值可知:在相同分布下,预测效果的优劣顺序是基于EGARCH、PGARCH、GARCH下的动态VaR模型;在每类波动率模型中,FSH-VaR、GPD-VaR模型优于SGT-VaR、GED-VaR模型;12种动态VaR模型中预测效果最差的是GARCH-GED模型。
表3给出了置信水平为97.5%下的动态VaR模型检验。当伴随概率α=2.5%时,Lruc检验、Lrind检验和DQ检验对应的拒绝零假设的边界值分别为
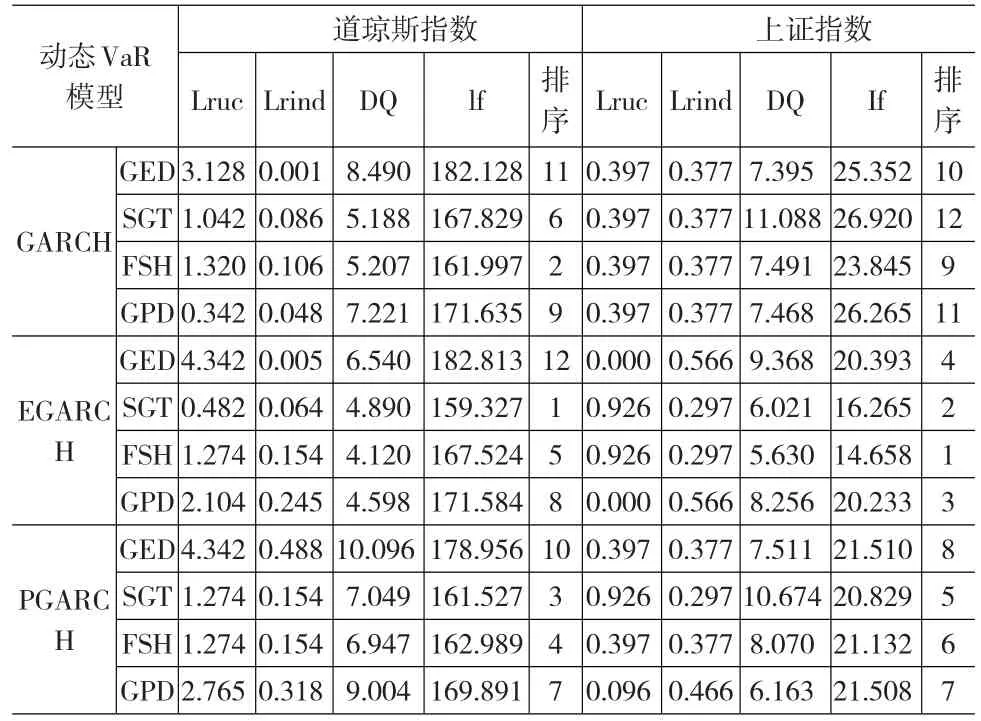
表3 置信水平97.5%下的动态VaR模型检验
由表3可知,在置信水平为97.5%时,12种模型都通过了准确性检验,具有可行性。根据损失函数lf的值可以看出,在相同分布下,动态VaR模型中风险度量的准确程度最差的是基于GARCH下的动态VaR模型;在EGARCH和PGARCH模型中,SGT-VaR更能准确的描绘市场,优于半参数法的FSH-VaR、GPD-VaR模型,但并不显著,预测能力最差的仍是GED-VaR模型。
表4给出了置信水平为95%下的动态VaR模型检验,当伴随概率α=5%时,Lruc检验、Lrind检验和DQ检验对应的拒绝零假设的边界值分别为
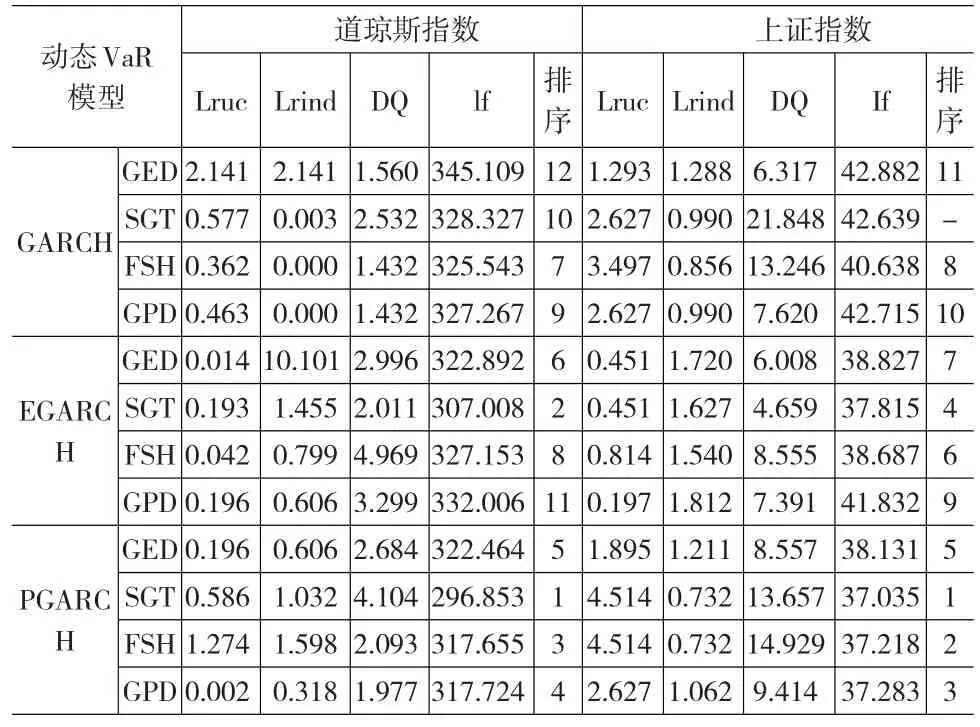
表4 置信水平95%下的样本外动态VaR模型检验
由表4可知,在置信水平为95%下,对于道琼斯指数,组合的12种模型都通过了第一阶段准确性检验,模型具有可行性;对于上证指数,GARCH-SGT-VaR没有通过检验。根据损失函数lf的值,在相同分布下,不同GARCH模型的动态VaR模型优劣顺序是基于PGARCH、EGARCH、GARCH下的动态VaR模型;对于EGARCH和PGARCH模型而言,预测准确程度最差的GED-VaR模型,参数法的SGT-VaR模型优于半参数法的FSH-VaR、GPD-VaR模型;12种模型中风险度量准确程度最高的模型是PGARCH-SGT-VaR模型,最差的是GARCH-GED-VaR模型。
4 结论
本文对GARCH族模型中三个经典的模型:GARCH模型、EGARCH模型和PGARCH模型的风险收益率取了三种不同分布,并运用了FSH方法组合了12种动态VaR模型,并采用道琼斯股票指数和上证指数检验了12种模型在不同置信水平下的准确性和风险度量能力的优劣,由实证分析得出以下结论:
第一,道琼斯股票市场和上证股票市场的收益率序列都具有尖峰厚尾的特点,不服从一般的正态分布。因此,在实际操作中,以正态分布计算VaR值的机构或个人需提高风险意识,增强抵抗风险的能力。
第二,在相同分布假设下,GARCH模型的风险度量能力最弱,EGARCH模型和PGARCH模型能更好地刻画市场的波动情况。但在不同的置信水平下,EGARCH模型和PGARCH模型的度量能力也有差异,在置信水平为99.5%时,EGARCH模型的风险度量能力最好,在置信水平为95%,PGARCH模型的风险度量能力最好。
第三,对于GARCH模型、EGARCH模型和PGARCH模型,在采用参数法和非参数法分别对市场风险进行估计时,假定市场收益率服从GED分布的模型市场风险度量能力最弱,这表明在这些方法中GED分布不能准确的描述市场,SGT-VaR、FSH-VaR和GPD-VaR能更好地拟合市场。在置信水平99.5%下,半参数模型(FSH-VaR,GPD-VaR)比参数模型(SGT-VaR)风险度量能力好;在置信水平97.5%下,参数模型(SGT-VaR)比半参数模型(FSH-VaR,GPD-VaR)风险度量能力略好,但并不显著;在置信水平95%下,参数模型(SGT-VaR)风险度量能力优于半参数模型(FSH-VaR,GPD-VaR)。可见,在参数模型和非参数模型都能较好的拟合市场时,置信水平越高,半参数模型(FSH-VaR,GPD-VaR)的风险度量能力越强,置信水平较低时,参数模型(SGT-VaR)的风险度量的准确程度优于半参数模型。
[1]Bali T,Theodossiou P.A Conditional-SGT-VaR Approach With Al⁃ternative GARCH Models[J].Annals of Research,2007,(151).
[2]Balkema A,de Haan L.Residual Life at Great Age[J].Annals of Prob⁃ability,1974,(2).
[3]Barone Adesi G,Giannopoulos K,Vosper L.VaR Without Correla⁃tions for Nonlinear Portfolios[J].Journal of Futures Markets,1999, (19).
[4]Bekiros S,Georgoutsos D.Estimation of Value at Risk by Extreme Value and Conventional Methods:A Comparative Evaluation of Their Predictive Per-Formance[J].Journal of International Financial Mar⁃kets,Institutions&Money,2005,15(3).
[5]Chen Q,Chen R.Method of Value-at-Risk and Empirical Research for Shanghai Stock Market[J].Procedia Computer Science,2013,(17).
[6]Cheng W,Hung J.Skewness and Leptokurtosis in GARCH-typed VaR Estimation of Petroleum and Metal Asset Returns[J].Journal of Empirical Finance,2011,(18).
[7]Christoffersen P.Evaluating Interval Forecasting[J].International Eco⁃ nomic Review,1998,(38).
[8]Engle R F,Manganelli S.CAViaR:Conditional Autoregressive Value at Risk by Regression Quantiles[J].Journal of Business and Economic Statistics,2004,(22).
[9]Fisher R,Tippett L.Limiting Forms of the Frequency Distribution of The Largest or Smallest Member of a Sample[J].Proceedings of the Cambridge Philosophical Society,1928,(24).
[10]Kupiec P.Techniques for Verifying the Accuracy of Risk Measure⁃ment Models[J].Journal of Derivatives,1995,(2).
[11]Marimoutou V,Raggad B,Trabelsi A.Extreme Value Theory and Val⁃ue at Risk:Application to Oil Market[J].Energy Economics,2009, (31).
[12]McNeil A,Frey R.Estimation of Tail-Related Risk Measures for Heteroscedasticity Financial Time Series:An Extreme Value Ap⁃proach[J].Journal of Empirical Finance,2000,(7).
[13]Polanski A,Stoja E.Incorporating Higher Moments Into Val⁃ue-at-risk Forecasting[J].Journal of Forecasting,2010,(29).
[14]Trenca I.The Use in Banks of VaR Method in Market Risk Manage⁃ment[J]Economic Sciences Series 2009.
[15]Zikovic S,Aktan B.Global Financial Crisis and Var Performance in Emerging Markets:A Case of EU Candidate States-Turkey and Croatia[J].Journal of Economics and Business,2009,(27).
[16]高莹,周鑫,金秀.GARCH模型在动态VaR中的应用[J].东北大学学报(自然科学报),2008,29(4).
[17]徐炜,黄炎龙.GARCH模型和VaR的度量研究[J].数量经济技术经济研究,2008,(1).
[18]朱慧明等.基于序数空间的行业间战略相对风险度量[J].统计与决策,2012,(13).
(责任编辑/易永生)
F830
A
1002-6487(2016)23-0015-06
全国统计科学研究重点项目(2015LZ54);安徽省高校自然科学重点基金项目(KJ2016A278);安徽省软科学项目(1502052039);安徽师范大学哲学社会科学繁荣发展计划首批重大项目(FRZD201302);2014年安徽师范大学特色优势研究领域建设项目
张 琼(1976—),女,安徽枞阳人,博士,副教授,研究方向:经济统计。

