基于变步长梯形算法GM(1,1)模型背景值的优化

肖利哲，王学娟

（哈尔滨理工大学 管理学院，哈尔滨 150040）

基于变步长梯形算法GM(1,1)模型背景值的优化

肖利哲，王学娟

（哈尔滨理工大学 管理学院，哈尔滨 150040）

文章从GM(1,1)建模机理及背景值形成过程出发，分析出对于具有明显指数规律的一次累加生成序列，GM(1,1)有时会出现预测误差较大的情况，并得出背景值的构造方法是造成这种误差的重要原因之一。利用拉格朗日插值函数和变步长梯形算法对背景值进行优化，通过对变步长梯形算法中步长大小的变化，形成了一种新的背景值构造方法，可使由背景值构成的误差降低。

GM(1,1)模型；背景值；变步长梯形算法

0 引言

灰色系统是研究少数据、贫信息等不确定性问题的理论，灰色预测是灰色系统理论的主要研究内容之一，广泛应用于多个领域，而GM(1,1)模型是灰色预测的核心内容[1]，长期以来受到很多学者关注，但在研究过程中发现该模型有时会出现预测精确度不高的问题，因此对该问题做了很多研究。谭冠军[2]初步分析了GM(1,1)模型背景值构造所产生的误差，并给出新的构造方法。王钟羡，张怡等[3，4]根据GM(1,1)模型的指数特性，通过在定区间上求积分，给出了背景值的一个计算公式，在一定程度上提高了模型的预测精度。杨华龙等人[5]应用自动寻优定权方法，根据原始数据的模拟值与真实值之间的最小离差平方和来确定最终权重，但计算过程较为繁琐。李俊峰，戴文战[6]利用Newton-Cotes公式计算背景值，但n较大时，高次插值将出现Range现象，造成较大误差。唐万梅，向长合[7]则基于二次插值来构造背景值，该方法避免了Range现象，但预测精度难以保证。

根据以上学者的研究，本文从一次累加生成序列的指数规律角度出发，利用拉格朗日插值函数以及变步长梯形算法，对背景值进行优化，使GM(1,1)模型不仅适用于指数规律较弱的数据序列，也适用于指数规律较强数据序列。

1 GM(1,1)建模机理及误差分析

1.1 GM(1,1)建模机理

GM(1,1)建模过程是将无规律的原始数据通过累加生成得到具有灰指数规律的数据序列，利用一阶线性微分方程的指数解形式来拟合x(1)() t进行建模，将得到的数据进行累减还原，再进行预测。定义1:设原始数据则一次累加生成序列为，简称1-AGO，其中

由于分析的数据是离散的，为求解参数a、b，将该一阶线性微分方程以定积分形式离散化，即：

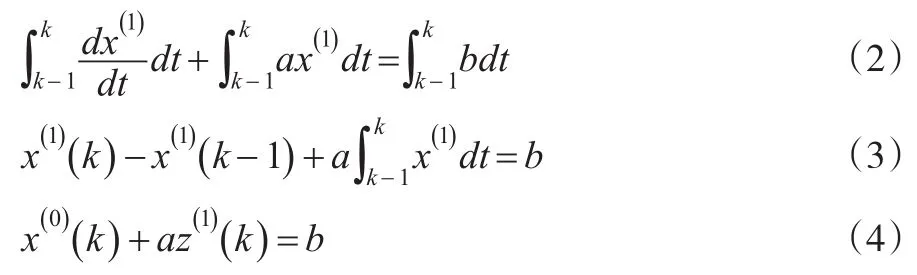
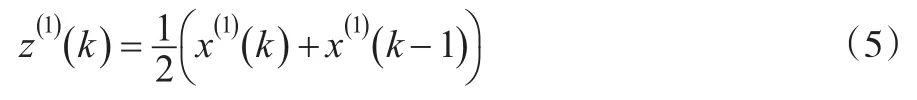
根据其离散形式，从积分几何角度出发，求解GM(1,1)模型背景值就是求解该定积分的过程。

定理2：设x(0)，x(1)如定义1所示，若令Y和B分别为下式：

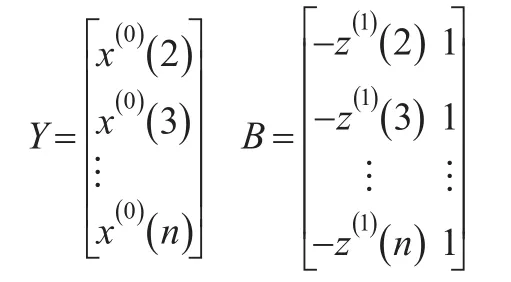
则GM(1,1)模型的最小二乘估计参数列为：

以x(o)(1)为初始值计算GM(1,1)的时间响应序列为：

其一次累减还原值为：

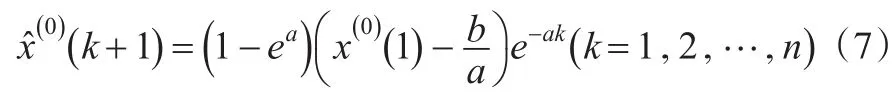
从以上的求解过程可以看出，参数a、b是影响GM(1, 1)模型预测精度的直接影响因素，而背景值z(1)(k)的构成方式又决定a、b的取值。因此科学合理的构造背景值，将有效提高模型的预测精度。

1.2 GM(1,1)模型误差分析

2 GM(1,1)模型背景值的优化

2.1 背景值优化方法构建

根据以上误差来源分析，针对1-AGO指数规律较强的数据序列，从背景值形成的积分几何意义出发，在积分区间[k -1，k]上插入适当的点，此处采用拉格朗日函数进行插值，近似得到x(1)(t)在插值点处函数值。并结合变步长梯形算法，通过选取合适的步长，即在对每个积分区间进行m等分时，选取合适的m值，用m个小梯形面积之和来近似代替曲边梯形面积。以小区间向下凹为例说明，如图1所示。

图1 面积逼近示意图

若函数 y=f(x)在[a ，b]上有定义，m+1个节点a=x0＜…＜xm=b处的值已知，则Lm(xj)=yj(j=0，1，…，m)。

则称此m+1个多项式l0(x)，l1(x)，…，lm(x)为节点x0＜…＜xm的m次插值基函数。可得m次插值基函数为：

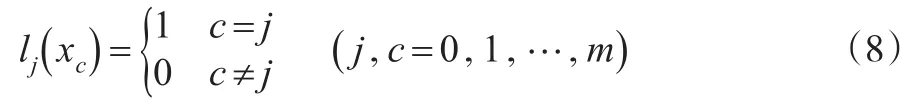
因此满足式⑻的插值多项式Lm(x)可表示为：

式⑼称为拉格朗日插值函数，简称Lm。

定义3：设将[ ] a，b分为m等分，共有m+1个节点，如果将求积区间再二分一次，则分点增至2m+1个，而每个子区间[ ] xd，xd+1经过二分只增加一个分点，即xd+1)，其中xd=a+ih;i=0，1，…，m;使用复化梯形公式求得该子区间上的积分值为：

式（11）给出了Tm与T2m之间的递推关系，方便计算机编程，减少了计算量，由此可见变步长梯形算法为复化梯形公式的逐次分半算法，下面讨论如何确定等分数m。

本文通过m计算背景值 z(1)(k )，以z(1)(k)确定a、b以得到拟合函数由与x(0)(k)计算相对误差ε(k)及平均相对误差。m在变化过程中使z(1)(k)、ε(k)、¯依次变化，最终使在变化过程中达到最小，选择此时m。

根据1-AGO波动性，由这些点拟合的Lm呈现凹凸变化的趋势，如图2所示。在对小区间进行等距划分并插值时，不能使每个小区间上的m个小梯形面积之和都更接近定积分值，相应的利用重构的z(1)(k)建模预测，不能使每个ε(k)都降低，进而使ε¯随ε(k)变化程度而改变。

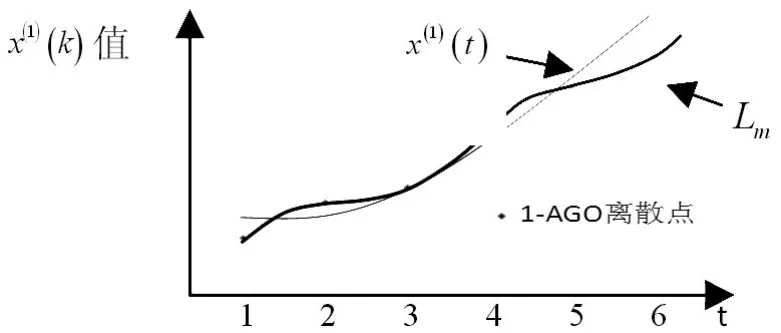
图2 曲线拟合图

②若且选择m=m1时计算背景值。

③若则继续增大m，直至某个m值，设为m*，若继续增大m，则¯增大。以m*计算背景值。

当原始数据为非波动性数据序列且1-AGO指数规律越明显时，则Lm整体向下凹或向上凸，可使Lm与x(1)(t)变化趋势更接近，则ε¯可降低的空间就越大。

下面以实证部分数据说明z(1)(k)、ε(k)、¯之间变化关系。

如表1所示，随m增大z(1)(k)均在减小，相应的ε(2)增大，ε(3)，ε(6)减小，ε(4)，ε(5)先减小后增大，且¯逐渐减小，当m=8时¯达到最小，以此m对应的z(1)(k)计算参数a、b。

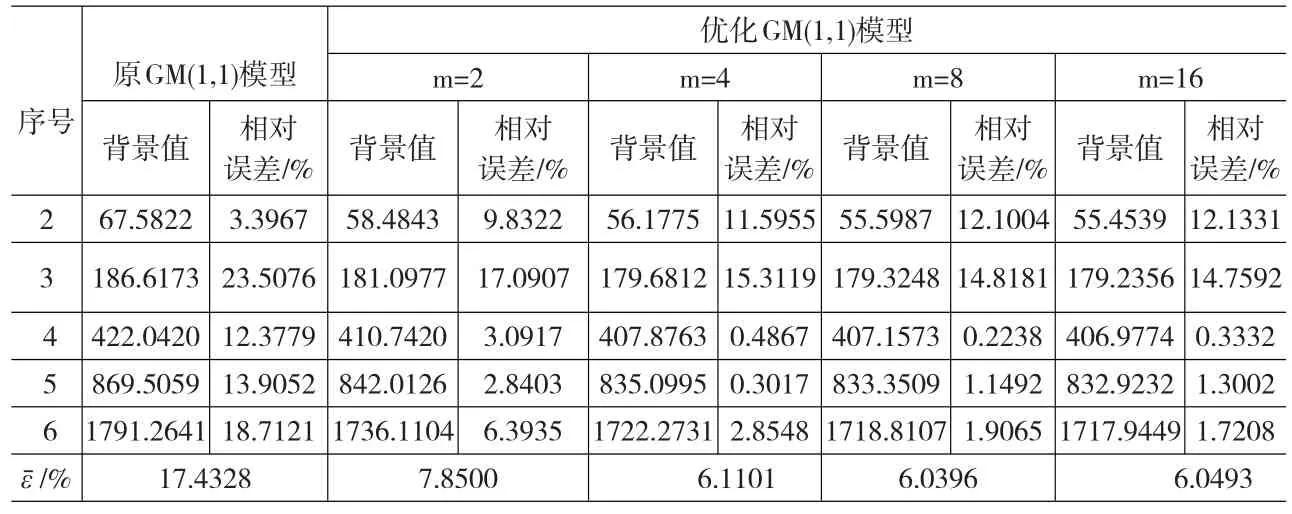
表1 背景值与相对误差及平均相对误差变化对照

2.2 基于优化背景值的GM(1,1)模型的改进

⑴计算ρ(k)与σ(k)分析指数规律，并利用软件计算原模型平均相对误差设定初始值m1，由Lm函数计算区间[k ，k+1]上m1等分点处的函数值。

⑵根据变步长梯形算法，由m1值及插值点处的函数值计算背景值。

⑶根据定理2计算参数a、b的值，并根据式⑺求得原始数据的模拟值。

⑷计算模拟值的相对误差ε1(k)及整体平均相对误差

表2 原模型与优化模型工业总产值模拟预测比较

3 实例分析

本文以上海市六五至十一五期间工业总产值作为基本数据说明模型改进情况，原始数据见表2所示。

⑴分别计算ρ(k )与σ(1)(k)的值，得出其1-AGO具有较强的指数规律。并计算原模型平均相对误差，见表2。

⑵令初值m=2，插入一个点，并以区间[1 ，2]为例计算插值及背景值，其他区间类似。给出Lm函数：

L6(x)=0.1406x5+4.4821x4-51.1969x3+236.5319x2-357.8253x+202.9591

⑶计算背景值

同理计算z(1)(k)，k=3，4，5，6时的值，见表1。将得到的背景值带入到GM(1,1)模型，得到m=2时模拟预测值，并分别取m=4、8、16,计算不同m值时的背景值，并代入GM (1,1)模型计算模拟值，与原模型进行比较，见表2。

如表2所示，当m取8时模型的平均相对误差最小，选择m*=8时的背景值计算a、b，并利用式⑺进行预测。

GM(1,1)模型有三种检验方法：残差检验、关联度检验以及均方差比检验，本文采用均方差比检验方法，如下:

设原始数据序列x(0)及残差序列的均值和方差分别为：

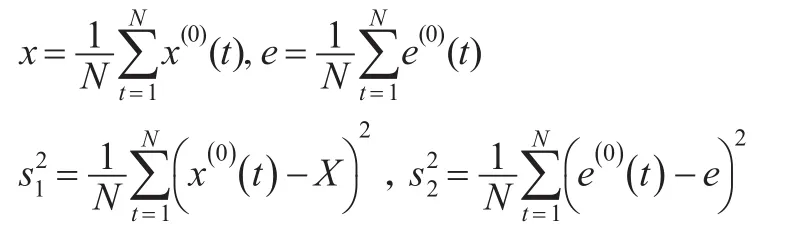
模型的精度由P和c共同描述，一般分为四个等级，一级：0.95≤p，c≤0.35；二级：0.80≤p＜0.95，0.3＜c≤0.5；三级：0.70≤p＜0.80，0.5＜c≤0.65；四级：P＜0.70，0.65＜c。对模型的精度进行检验，经过计算得到 p=1，c=0.01。该模拟预测的精度属于一级，精度较高。

4 总结

本文针对一次累加生成指数规律明显的数据序列，利用拉格朗日插值函数以及变步长梯形算法，提出了新的背景值构造方法。在变步长梯形算法中，随着步长的变化，也就是等分数m取值的不同，预测结果的平均相对误差会随之变化。变化过程中会有一个m*使平均相对误差达到最小或其差值小于某一特定值，以m*计算模型背景值。若m*=0则使用原模型，若m*＞0表示优化了GM(1,1)模型，提高了模型的预测精度。通常，当1-AGO指数规律越明显时，m*应越大，随指数规律的减弱m*变小，当m*=0时，即使用原模型。根据重构背景值的GM(1,1)模型，利用上海市六五至十一五期间工业生产总值进行模拟预测，证明该优化模型可以提高指数规律较强的1-AGO的预测精度，并具有一定的理论意义与应用价值。

[1]刘思峰，党耀国.灰色系统理论及其应用[M].北京：科学出版社，2010.

[2]谭冠军.GM(1,1)模型的背景值构造方法和应用(Ⅰ)[J].系统工程理论与实践，2000，(4).

[3]王钟羡，吴春笃.GM(1,1)改进模型及其应用[J].数学的实践与认识，2003，33(9).

[4]张怡,魏勇,熊常伟.灰色模型GM(1,1)的一种新优化方法[J].系统工程理论与实践，2007，(4).

[5]杨华龙，刘金霞，郑斌.灰色预测GM(1,1)模型的改进及应用[J].数学的实践与认识，2011，41(23).

[6]李俊峰，戴文战.基于插值和Newton-Cores公式的GM(1,1)模型的背景值构造新方法与应用[J].系统工程理论与实践，2004，(10).

[7]唐万梅，向长合.基于二次插值的GM(1,1)模型预测方法的改进[J].中国管理科学，2006，14(6).

（责任编辑/易永生）

N941.5

A

1002-6487（2016）23-0008-04

黑龙江省高教综合改革试点专项课题资助（JG2013010288）

肖利哲（1961—），男，黑龙江哈尔滨人，硕士，教授，研究方向：统计学、人力资源。

王学娟（1989—），女，河北廊坊人，硕士研究生，研究方向：人力资源管理。