考虑决策主体风险偏好的连锁企业物流系统优化研究
周宝刚,赵宏霞,刘安业
(渤海大学 管理学院,辽宁 锦州 121013)
考虑决策主体风险偏好的连锁企业物流系统优化研究
周宝刚,赵宏霞,刘安业
(渤海大学 管理学院,辽宁 锦州 121013)
连锁企业在面对各种不确定性因素时会表现不同的风险偏好。文章主要考虑连锁物流系统中供应商的供应风险、城市配送中心的运营风险和连锁门店的需求风险。将风险事件的可信性置信水平转换为风险偏好系数,研究决策主体的风险偏好对连锁企业物流系统的各项指标和整体性能的影响。结果表明,随着决策主体风险偏好程度的增大物流系统的总成本目标值逐渐减小,并最终影响采购与配送决策。
连锁企业;物流系统;决策主体;风险偏好;置信水平
0 引言
连锁企业作为连锁供应链物流系统中的决策主体,其风险偏好程度对系统的各项指标和整体性能将产生重要影响。在不确定的风险环境下,大多研究假设供应链中成员企业是风险厌恶型或风险中性型的,很少考虑决策主体的风险偏好的变化对供应链系统决策与绩效的影响[1]。近年来,与决策主体风险偏好相关的研究主要集中在供应链的契约设计和协调优化问题上,研究的主要对象仍然是具有风险规避行为的风险厌恶类型企业[2,3]。在现有文献中,基于决策主体不同风险偏好视角下的供应链优化与协调方面的研究还比较少,研究方法主要采用期望效用、均值-方差、和风险价值模型进行风险度量[4,5]。在实际的运营与管理过程中,企业的供应链物流系统总是面临着各种不确定性的风险,如供应风险、自身运营风险和市场需求风险。即使面对同样的风险环境,由于决策主体的风险偏好不同,也会产生不同的决策行为,选择不同的决策方案,以此获得满足自身心理偏好的期望结果。
本文应用模糊可信性理论研究了连锁企业作为决策主体,在不同风险偏好下的物流系统设计与优化问题。决策主体的风险偏好既包括了风险厌恶、风险中性和风险追求三种典型类型,又涵盖了从风险厌恶到风险追求之间的任何一种风险偏好程度。揭示了决策主体风险偏好程度变化对连锁企业的采购量、配送量、物流系统配置以及整体绩效的影响。
1 符号说明与模型设定
本文的研究对象是以连锁企业为核心决策主体,包含多个供应商、多个城市配送中心和多个连锁门店的连锁物流系统。在物流系统设计与规划中,一项重要的考虑因素是识别主要成本动因,即在进行系统优化时要重点分析发生了哪些物流成本[6]。连锁企业作为核心决策者所要执行的决策是选择哪些供应商采购一种产品、经由哪些配送中心配送至具有需求的门店,使得连锁物流系统的总成本最小。考虑供应商的产品价格、质量、供应能力,城市配送中心的处理能力和连锁门店的需求为模糊风险因素,研究考虑决策主体风险偏好下的连锁企业物流系统的设计与集成优化问题。
1.1 符号说明
参数:i表示供应商,i=1,2,...,I;k表示城市配送中心,k=1,2,...,K;l表示连锁门店,l=1,2,...,L;ci表示供应商i的单位产品价格;FCi表示在供应商i的订货固定成本;FDk表示城市配送中心k运营启动成本,即固定成本;hk表示城市配送中心k的单位库存持有成本,即变动成本;SDik表示供应商i将产品运输到城市配送中心k的单位运输成本;DRkl表示城市配送中心k将产品配送到连锁门店l的单位配送成本;qi表示供应商i的质量合格率;q表示连锁企业根据产品质量标准要求的质量合格率;Dl表示一定时期内的连锁门店l的产品市场需求量;Ci表示供应商i的最大供应能力;Oi表示在供应商i的最小订货量;Wk表示城市配送中心k的处理能力;I表示可选择的供应商数量;P表示城市配送中心的启用数量。
决策变量:xik表示城市配送中心k在供应商i处的产品采购数量;ykl表示城市配送中心k向连锁门店l的产品配送数量;Xi:0~1变量,连锁企业在供应商i处采购为于1,否则等于0;Zk:0~1变量,城市配送中心k运营启动为1,否者为0;Ykl:0~1变量,城市配送中心k为门店l提供配送服务为1,否则为0。
1.2 模型设定
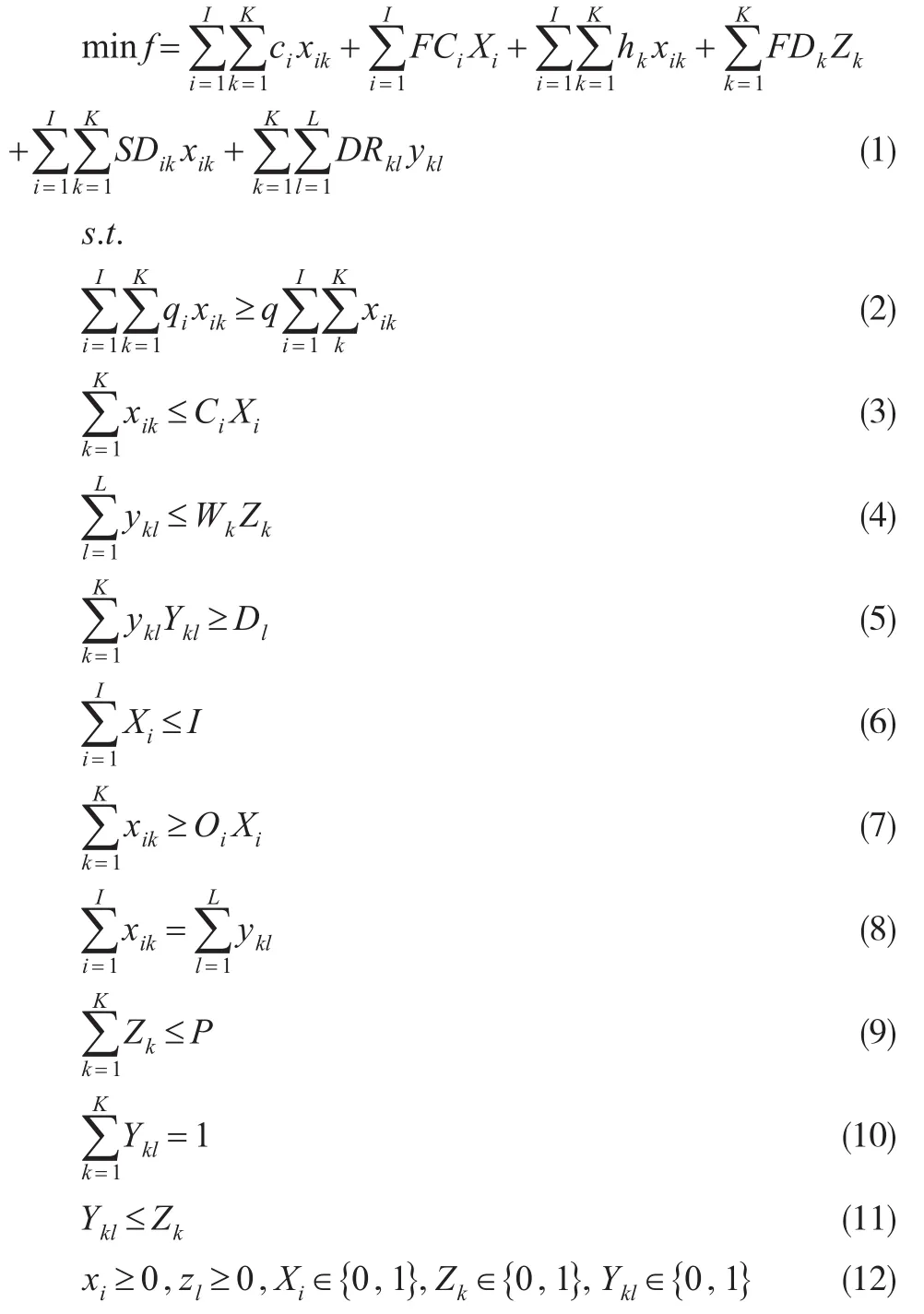
式(1)为最小化连锁物流系统总成本目标,包含六项成本:第一项为连锁企业的采购成本,第二项为供应商选择成本,第三项为城市配送中心运营的变动成本,第四项为城市配送中心运营的固定成本,第五项为供应商将产品运输到城市配送中心的运输成本,第六项为城市配送中心将产品运送到连锁门店的配送成本;式(2)为要求供应商的产品质量约束,多个供应商提供的产品质量要满足连锁企业的总体产品质量要求;式(3)为供应商自身的供应能力约束,在选择某一供应商的前提下,供应商所能提供的最大产品数量不大于其供应能力;式(4)为城市配送中心的仓储能力约束,城市配送中心能够中转储存的产品数量不超过为此类产品预设的最大库存水平;式(5)为满足连锁门店的产品需求量约束,城市配送中心的产品配送数量要满足连锁门店的产品需求数量;式(6)为供应商选择数量约束,连锁企业在综合考虑供应商的价格、质量和供应能力风险后的选择供应商上限数量;式(7)为最低订货量约束,连锁企业在已选的供应商处订购产品的最低数量;式(8)为城市配送中心产品数量平衡约束,供应商与城市配送中心之间的产品运输数量等于城市配送中心与连锁门店之间的产品配送数量;式(9)为城市配送中心启用数量约束,多个配送中心为此类产品服务所启用的最大数量;式(10)和式(11)为城市配送中心为连锁门店服务的单源配送约束,即一个城市配送中心只能为一个连锁门店配送,而一个连锁门店可由多个城市配送中心为其配送;式(12)为连锁物流系统决策变量取值约束。
2 风险偏好下的物流系统优化模型
2.1 可信性理论与模糊机会约束规划
(1)可信性公理与可信性分布
假设Θ为非空集合,Ρ(Θ)表示Θ的幂集。Ρ(Θ)中的每一个元素称为一个事件,为了给出可信性的公理化定义,必须分配给事件A一个测度数值Cr{A}表示A将要发生的可信性程度。为了确保可信性测度函数Cr{A}在实际应用中的合理性,必须满足下面4条公理。
公理1(均一性):Cr{Θ}=1;
公理2(单调性):Cr{A}≤Cr{B},当AÌB;
公理3(自对偶性):Cr{A}+Cr{Ac}=1,任一事件AÎΡ(Θ);
定义1:假设Θ为非空集合,Ρ(Θ)表示Θ的幂集,Cr为可信性测度,则三元组(Θ ,Ρ(Θ),Cr)称为可信性空间。
定义2:假设ξ为从可信性空间(Θ ,Ρ(Θ),Cr)到实直线Â上的函数,则称ξ是一个模糊变量。
定义3:假设ξ为模糊变量,若函数Φ:[- ¥,+¥]®R:[0, 1]满足:
则Φ称为模糊变量ξ的可信性分布。
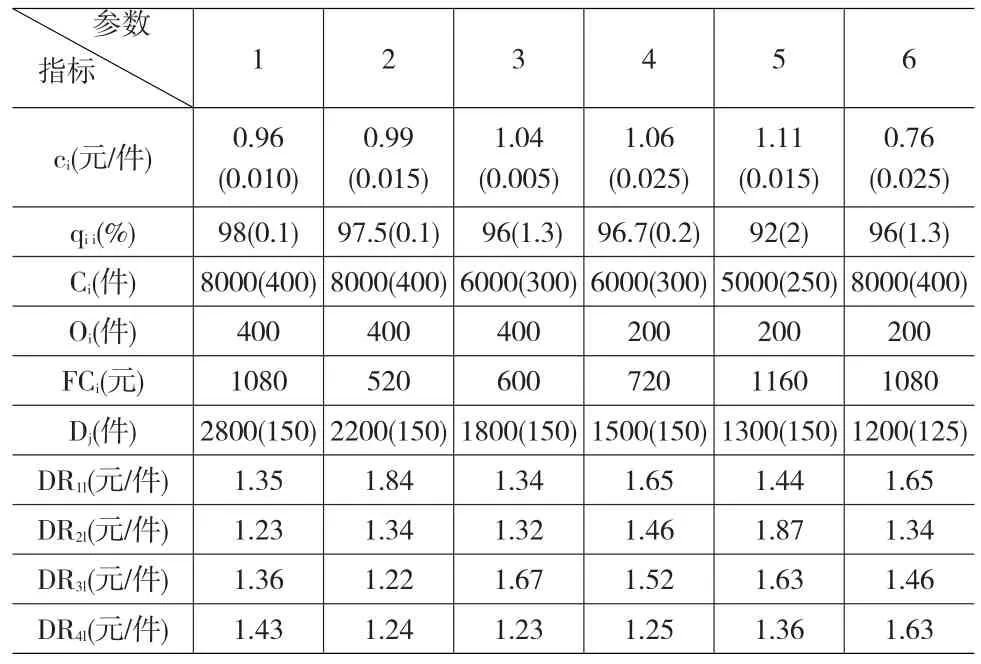
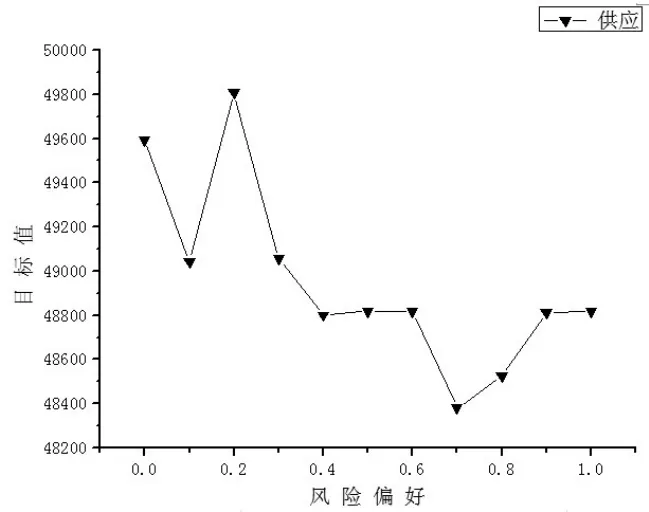
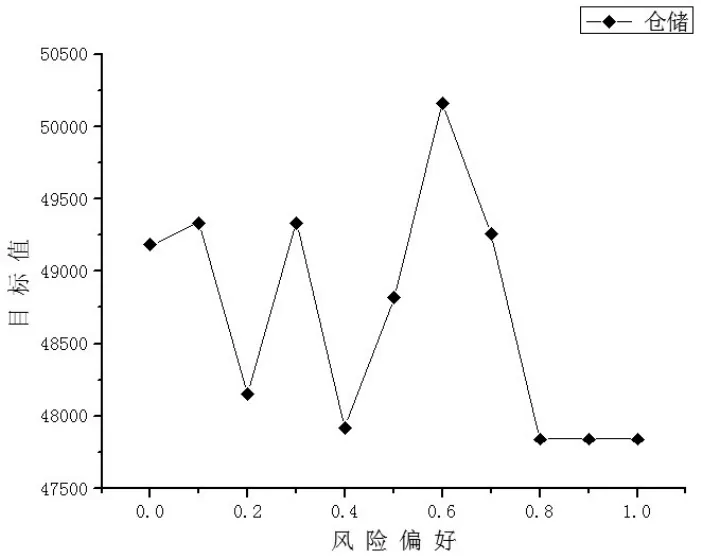
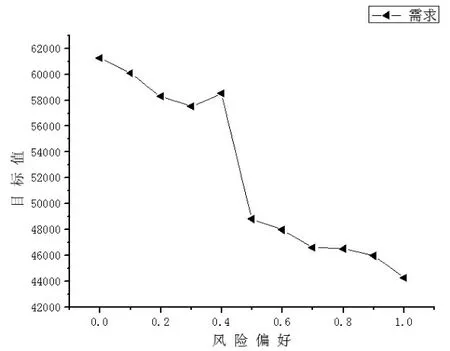
假设模糊变量ξ的隶属函数为μ(x),一个梯形模糊变量(a ,b,c,d),由清晰实数a 其可信性分布函数为: (2)模糊机会约束规划 基于可信性测度的模糊机会约束规划的基本思想是:在模糊环境中,决策主体希望规划中的约束条件以一定的置信水平成立的前提下来优化系统的目标函数。基于可信性测度的模糊机会约束规划的一般模型如式(14): 其中,x为决策向量,ξ为模糊参数向量,f(x ,ξ)为目标函数,gj(x ,ξ)为条件约束函数。β和αj分别为决策者对目标和条件机会约束预先设定的置信水平。 基于可信性测度的模糊机会约束规划求解的最有效方法就是依据决策者预先设定的模糊事件成立的置信水平将机会约束规划转化为一个清晰等价的线性规划。本文采用乐观值和悲观值两个关键指标值进行清晰转化。,称为ξ的α乐观值;其含义为模糊变量ξ不低于乐观值ξsup(α)的可信性为α,即乐观值ξsup(α)是模糊变量ξ以可信性α所取的值中最大的;Cr{ξ ³r}³α,清晰等价形式为r≤ξsup(α)。ξinf(α)=inf {r|Cr{ξ ≤r}³α},称为ξ的α悲观值;其含义为模糊变量ξ不大于悲观值ξinf(α)的可信性为α,即α悲观值ξinf(α)是模糊变量ξ以可信性α所取值中最小的;Cr{ξ ≤r}³α,清晰等价形式为r³ξinf(α)。 基于可信性测度的模糊机会约束的清晰等价约束可通过上述情况进行转化。 2.2 机会约束规划模型 在连锁企业物流系统的实际运作过程中,各种数据参数或风险事件很难以精确数值形式给出,即连锁物流系统存在不确定性因素。如果这些不确定的数据由于信息的不完备性产生,则这些数据就是一种基于可信性的模糊数据。在这种情况下,连锁物流系统中的决策主体可依据少量的信息经主观分析判断,将这些不确定的参数或风险事件数据处理为模糊变量[7]。描述包含模糊变量的风险事件发生的可信性程度水平,可表示为决策主体对不确定事件成立所持有的风险态度或风险偏好。研究将连锁企业供应链物流系统中的供应商的价格、质量合格率、供应能力和城市配送中心的仓储能力以及连锁门店的需求均设为模糊变量;因此,将式(1)—式(12)决策模型转化为基于可信性理论的考虑决策主体风险偏好的连锁企业物流系统的机会规划模型。 其他约束与式(7)至式(12)相同。 本文中,连锁物流系统的各种不确定的风险因素均假设为梯形模糊变量,机会约束的α乐观值和α悲观值为以下两式: Cr(.)表示连锁物流系统中模糊风险事件发生的可信性测度函数,α为决策主体以主观偏好预设的置信水平,Cr(.)³α为基于可信性测度的机会约束条件,含义为连锁企业作为决策主体期望的模糊风险事件以预设的置信水平α成立。 3.1 案例描述 本文所研究案例内容在已有的文献基础上进行了一定修改和完善[8,9]。连锁企业在某一城市区域内拥有4个配送中心和6个连锁门店,可向6个供应商采购一种产品。连锁企业作为物流系统中的决策主体需要进行的决策是选择优质的供应商,启用恰当的城市配送中心将产品配送至具有不确定需求的连锁门店。 城市配送中心的仓储能力、库存变动成本、运营固定成本和供应商-城市配送中心运输成本等相关数据如表1所示。供应商的产品价格、质量合格率、自身供应能力、要求最小订货量、选择的固定订货成本,连锁门店的市场需求以及城市配送中心与连锁门店之间的配送成本等相关数据如表2所示。表1和表2中单元格内存在μ(σ)类型数据,其中μ、σ分别为数据的均值和标准差,但决策者并不能准确的获知数据服从何种概率分布。这类数据是由于信息的不完备性造成的,因此,本文将通过数据的均值和标准差转化为梯形模糊变量(a ,b,c,d),转化规则为a=μ-2σ,b=μ-σ,c=μ+σ,d=μ+2σ。连锁企业选择供应商最多数量 I=4,城市配送中心最多启用数量P=3,要求的产品质量合格率q=0.96。 表1 城市配送中心和供应商-城市配送中心运输成本相关数据 表2 供应商、连锁门店和城市配送中心-连锁门店配送成本相关数据 3.2 数值分析 将案例中相关数据代入由基于可信性测度机会约束规划转化的清晰等价线性规划模型中,并考虑风险偏好系数的变化,即可研究和分析连锁企业的风险偏好对物流系统各项指标和系统目标的影响。首先,预设其他不确定因素为风险中性(风险偏好值为0.5),分别研究决策者针对某一特定不确定因素的风险偏好程度变化对连锁物流系统目标值的影响,如图1至图5所示。 图1 系统目标值随价格因素的风险偏好变化 在图1中,系统目标值随价格因素的风险偏好增大逐渐变小。由于决策主体预期的产品价格是逐渐减小的,导致在不同供应商处的订货量发生变化,采购成本减少,但可能导致运输和配送成本的增加,所以目标值时而减少时而增大,但最终趋势是减小的。 图2 系统目标值随供应因素的风险偏好变化 在图2中,系统目标值随质量因素的风险偏好变化波动较大。由于决策主体预期的产品质量是逐渐增大的,供应商1和2的产品质量始终能保证决策者最低质量标准0.96的要求并满足需求,因此订货数量在供应商1和2之间变化分配,并且配送成本也在发生变化,所以目标值也是时而减少时而增大,没有总体减少或增大趋势,说明目标值对质量因素风险偏好的变化不敏感。 图3 系统目标值随供应因素的风险偏好变化 在图3中,系统目标值随供应因素的风险偏好增大逐渐减小。由于决策主体预期的供应能力是逐渐增大的,并且供应商1和2在各项指标都具有极好的优势,因此始终选择两者作为供应商,同时再选择具有运输和配送成本优势的配送中心,所以目标值的总体趋势是减小的。 图4 系统目标值随仓储因素的风险偏好变化 在图4中,系统目标值随仓储因素的风险偏好变化时大时小。由于决策主体预期的配送中心仓储能力是逐渐增大的,并且启动的配送中心在2、3和4之中选择两个或三个,相应的采购运输和分销配送成本也随之增大或减少,所以目标成本值也是时而减少时而增大,但最终的总体趋势是减少的。 图5 系统目标值随需求因素的风险偏好变化 在图5中,系统目标值随需求因素的风险偏好增大逐渐变小。由于决策主体预期的需求量是逐渐减小的,这将直接导致采购数量减少,同时减少运输和配送成本,因此目标值总体趋势是明显减小的,说明目标值对于需求因素风险态度的变化非常敏感。 下面研究决策者对不确定模糊事件的风险偏好从风险厌恶到风险中性再到风险追求过程中,连锁企业作为核心决策者的风险偏好变化对连锁物流系统网络结构和物流总成本目标值的影响。 当模糊机会约束置信水平全为1,决策主体为风险厌恶型时,最小化成本目标值 fˉ=63634,选择供应商1和2供货,启用配送中心1,2和3。当模糊机会约束置信水平全为0.5,决策主体为风险中性时,最小化总成本目标值fˉ=48816.5,选择供应商1和2供货,启用配送中心2、3和4。当模糊机会约束置信水平全为0,决策主体为风险追求时,最小化总成本目标值 fˉ=44332,选择供应商1和2供货,启用配送中心2和3。具体订货量与配送量见表3。 表3 不同风险偏好下的连锁物流系统的订货量与配送量 通过表3可以看出,决策主体无论在何种风险偏好下,都选择了供应商1和2;因为供应商1和2在满足供应能力等标准的情况下产品价格和质量合格率方面较其他供应商具有明显的优势。而在三种风险偏好下都启用了城市配送中心2和3,两个配送中心在单位库存变动成本和启用固定成本上都小于其他两个。 从图6中可以看出,连锁企业物流系统总成本目标值随决策主体对各个模糊因素整体风险偏好的变化趋势,正是对单个模糊因素风险偏好的变化状态相叠加的结果。其中只有对质量因素风险偏好的变化是不敏感的,对其余几个模糊因素的风险偏好变化都是逐渐或明显减小的,因此系统目标值随决策主体整体风险偏好的变化趋势为逐渐减小。 图6 连锁企业物流系统目标值随整体风险偏好变化趋势 本文提出了考虑决策主体风险偏好的连锁企业物流系统设计与优化问题,基于模糊可信性理论构建了连锁物流系统规划模型,求解了不同风险偏好下连锁企业采购、配送、物流网络配置以及系统目标的优化结果,通过数值计算与敏感性分析研究了决策主体的风险偏好变化对连锁物流系统总成本目标的影响。本研究不仅考虑了三种典型风险偏好类型,并且给出了处于任何中间状态的供应链物流系统总成本目标值。可以看出,总成本随着决策者风险偏好的变化存在减少或增加的波动,但总体趋势最终是减少的。风险厌恶型决策主体不愿意冒险去获取不确定的收益而选择规避风险行为,风险追求型决策主体因追求更小成本或更大收益而选择冒险行为,风险中性的决策者介于两种风险态度之间,研究结果更倾向于风险追求。 [1]马士华,李果.供应商产出随机下基于风险共享的供应链协同模型[J].计算机集成制造系统,2010,16(3). [2]王虹,周晶.具有风险规避参与者的双渠道供应链最优策略研究[J].计算机集成制造系统,2009,15(11). [3]林志炳,张岐山,蔡晨.风险厌恶假设下的供应链回购契约模型[J].预测,2010,(6). [4]于春云,赵希男,关志民,彭艳东,潘德惠.具有风险偏爱特性的供应链优化与协调模型[J].系统工程,2009,27(11). [5]于明进,王炬香,桑圣举.风险偏好下供应链收益共享契约机制研究[J].科学技术与工程,2008,8(22). [6]Kalcsics J,Nickel S,Puerto J,et al.Distribution Systems Design With Role Dependent Objectives[J].European Journal of Operational Re⁃search,2010,202(2). [7]计晓宇,邵震.基于不确定规划的供应链网络设计模型与算法[J].系统工程理论与实践,2007,(2). [8]Pokharel S.A Two Objective Model for Decision Making in a Supply Chain[J].International Journal of Production Economics,2008,111 (2). [9]Tuzkaya U R,Önüt S.A Holonic Approach Based Integration Method⁃ology for Transportation and Warehousing Functions of the Supply Network[J].Computers&Industrial Engineering,2009,56(2). (责任编辑/刘柳青) F274 A 1002-6487(2016)21-0044-05 国家自然科学基金资助项目(71401015;71201012);辽宁省社科联经济社会发展立项课题(2014lslktziyyjj-04) 周宝刚(1979—),男,辽宁凌海人,博士,副教授,研究方向:物流与供应链管理。 赵宏霞(1978—),女,内蒙古赤峰人,博士,副教授,研究方向:网络营销。 刘安业(1975—),男,黑龙江哈尔滨人,博士,副教授,研究方向:物流与供应链管理。

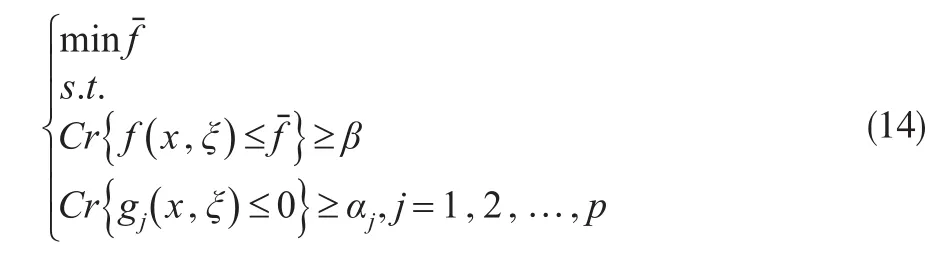



3 案例描述与数值分析





4 结论

