基于改进Black-Scholes模型的人力资本内在期权价值估计

廖特明，谭志勇

（西南石油大学 经济管理学院，成都 610500）

基于改进Black-Scholes模型的人力资本内在期权价值估计

廖特明，谭志勇

（西南石油大学 经济管理学院，成都 610500）

文章结合期望在职时间、人力资本映射资产价值的现金流现值等要素构建了企业人力资本内在价值基础期权折算模型，并结合叠期循环特性的人力资本内在价值期权化利益实现进行Black-Scholes模型的改进，从而进一步实施具备复合叠套特性的企业人力资本内在价值期权估计中的应用验证。同时，将基于Black-Scholes模型的企业人力资本期权价值层级的叠套演进行为以层级跳跃为判断依据进行折算，并利用期权价格的随机最优控制作为区间问题进行折算。结果证实：改进Black-Scholes模型在针对叠套以及跳跃行为的人力资本变动过程中，为企业的人力资本存留决策提供了较好的验证及测度价值，但在企业存在更为显著的人力资源动态调整期间的期权价值预测中，需要结合综合投入成本进行相应的人力资本期权价值估计。

改进Black-Scholes模型；人力资本；期权价值；估计；应用

0 引言

随着经济社会和产业结构调整的进一步发展，人力资本对于经济增长的影响和推动作用也得以逐步加深。这同时也意味着人力资本对于企业而言存在着越来越重要的价值意义。对于人力资本价值的估计，无论是企业自身还是学术界都开展了深入的分析，对于企业人力资本内在价值的剖析运用了很多丰富的理论和验证工具。而人力资本自身存在丰富的流动性和一定程度的价值权衡属性，因此，如何更为客观地反映人力资本对于企业经营管理乃至市场竞争生存的价值，对于企业战略实施，一个国家的产业发展都具有重要而深刻的意义。为此，本文从人力资本自身的流动性和人力资本绩效表现、属性变动等角度进行了人力资本内在价值的估计。

现有研究主要是针对以人力资本价值期权预测进行了模型选取，以及模型预测分析精度提升的论证，选用模型主要集中在基础Black-Scholes模型，同时对于存在叠套以及跳跃的人力资本要素属性，在其测度上缺乏适应调整，以及进一步的细分。为此，本文结合期望在职时间、人力资本映射资产价值的现金流现值等要素，构建了企业人力资本内在价值基础期权折算模型，并就人力资本要素期权价值现金流转换过程中的叠套甚至跳跃进行了参数与转化过程细分，并将其以层级跳跃为判断依据加以折算，形成针对企业人力资本内在期权价值的预测。

1 企业人力资本期权价值测度基本模型

根据上述分析可知，人力资本内在价值不同于一般意义上的实物期权、金融期权，从本质而言，企业人力资本期权属性上存在对应金融期权部分的当前价值，而该类期权在其价值部分可以对应其当前价值，也即是企业人力资源在期权属性上所产生的预期现金流对应现值。同时，以人力资本内在价值对应的期权投资现值来映射其金融期权中的证券市场价值，并按照这一期权距离到期日映射上述人力资本相应金融期权价值的人力资本在职时间，其中，这一在职时间指的是人力资本的期望在职时间。最后，需要说明的是人力资源内在价值映射到金融期权的另一个特性便是其作为期权物质的不确定性，本文将这种不确定性归纳为其作为期权收益的不确定性，从而可获得企业内部管理以及技术类型人力资本内在期权价值可以表示为：

式（1）中，S、X、t、θ、r分别对应企业人力资源在期权属性上所产生的预期现金流对应现值、由人力资本映射的金融期权中的证券价值的投资形式现值、人力资本的期望在职时间、各类型人力资本内在价值测度过程中的不确定性、人力资本价值折算过程中不存在风险部分的利率，C刻画的是上述各要素综合作用下的人力资本内在价值对应期权价值，由此，可获得上述人力资本内在期权价值为企业带来的利益：

当然，作为为企业带来利益的人力资本内在价值，其本身存在成本投入的特性，因为研究同样将涉及企业人力资本内在价值的各个成本因素加以与上述期权内在价值的综合分析，结合既有研究分析，主要选取企业人力资源的招聘与甄选、内部培训以及员工薪酬与福利方面支出的成本，将其总和设置为V，由此可以结合上述综合成本，借助X刻画的人力资本映射的金融期权中的证券价值的投资形式现值，将其描述为：

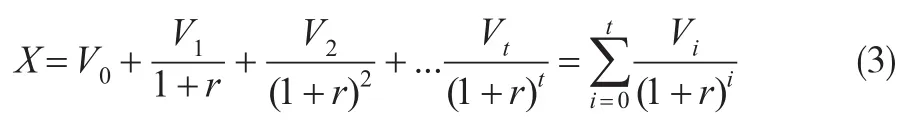
式（1）式（3）中t刻画的是单独人力资本也即是具体某类型人力资本（单一类型员工）的期望在职时间，其他参变量描述同上，由此结合式（1）至式（3）可以获得基于综合成本的企业人力资本内在价值及其对企业的期权收益，其中，人力资本在履职期间的执行期限映射成距离人力资本自身失去期权价值投资的距离，并以前述式（1）至式（3）中的t表示，人力资本内在价值以及波动期间不确定性仍分别由θ和t表示；企业人力资本在职时间按照期权形态的执行价格进行折算，映射成相关现金流X，而其相应的现金流现值则为人力资本所在企业对应标的资产价值S刻画，X和S分别映射成的人力资本期权形式折算为：

2 人力资本内在价值的期权定价与价值解析

2.1 人力资本其期权价值解析的分布函数

企业人力资本内在价值存在显著的金融期权属性，为此研究结合既有研究中的Black-Scholes模型，进行针对企业人力资本内在价值的期权定价与价值解析，具体描述为：

式（6）中N(x)、t、S分别对应刻画了参与企业人力资本内在价值折算的样本正态分布概率累积分布函数、具体某类型人力资本（单一类型员工）的期望在职时间、人力资本所在企业对应标的资产价值的现金流现值；X、C分别对应为某类型人力资本（单一类型员工）所映射的人力资本内在期权价值对应投资成本现值，及其实物期权为企业带来的价值利益，因此式（6）中的正态分布基期概率分布函数d1可以进一步演化为：

而对应的各累计期概率分布函数可以被表述为：

2.2 面向人力资本内在期权价值的Black-Schloes模型改进

人力资本内在价值映射至企业的实物期权的过程，需要企业进行进一步的决策，而这种决策赋予企业一定程度的物化资本或人力资本的投资抉择，但同样性质的期权仍存在不同性质的期权特性，即企业人力资本内在价值存在多期投资特征，无论是从企业的企业人力资源自身的流动还是其在企业内部供职期间所产生的期权现值，都涉及企业为之进行的人员招聘及甄选、内部培训以及员工薪酬与福利方面都产生相应的叠期成本，而这一成本也不仅构成企业人力资本内在价值的动态期权收益，更是制约每一期人力资本内在价值的期权现值。而从企业管理以及人力资本内在价值期权折现角度而言，也只有任意一期的企业人力资本内在价值完全实现期权现值利益目标，才能进一步适时开展下一期的人力资本内在价值期权折现目标的实施。而这种叠期循环特性的人力资本内在价值期权化利益实现，是以上一期成本目标的有效管理实现，从人力资本的期权价值折算角度则应属于复合人力资本期权现值，因而其实现是一种映射至企业的实物期权的过程的复合嵌套，具有实物期权形式特征的复合特性。

结合上述分析过程中关于企业人力资本内在价值的叠套复合特性，研究进行了Black-Scholes模型的改进，其中，人力资本内在价值的金融期权现金流映射为累计到期方式，也即是剔除了期权累计过程中生成人力资本期权溢价现金流，并将其后移至各期累计期权现金流中；同时，结合前述关于人力资本内在价值期权折算的成本分析，假定每一期的人力资本存续决策以上一期叠套折算后的期权超过综合成本为条件，对应的人力资本决策直接结果为人员续用或解聘，由此形成了区别于一般Black-Scholes模型的人力资本内在价值期权折算的叠套方式。

关于人力资本内在价值的叠套性质特征，研究以前期期权执行结果为本期人力资本决策依据，为此将这一决策依据归纳为当期人力资本期权属性综合特征，并将其用Π(t)表示，则上述分析中的期权叠套映射到企业人力资本期权价值可以表述为基于第T+i期的期望现金流，即：

由此综合式（7）至式（8）可获得以下关于改进Black-Scholes测度的企业人力资本内在价值叠套期权折算表达式，即：

式（10）中，dn刻画的是上述具备叠套特征的企业人力资本内在价值经过多次循环叠套的累积跳跃，由于需要配合前述的中间过程的人力资本期权价值剔除，为此，研究以S(t)刻画每次跳跃过程所对应的期权价值，而叠套过程同样存在前期人力资本期权价值的递增或衰减变动，为此，研究将叠套过程中非剔除部分的人力资本期权价值归纳为S(t±i)，S(t)、S(t±i)对应的最终累积人力资本期权价值被定义为两式对应在第T时序值。

2.3 改进Black-Scholes模型对企业人力资本内在价值期权估计实施步骤

研究给予改进Black-Scholes模型的人力资本期权动态现金流价值，即赋予每层次人力资本期权基期价值的折算方式，当企业运营过程中的人力资本期权价值外部干扰因素充足或足以影响当期人力资本期权现金流时，设定一个包含λ参数的泊松随机过程，且其对应的当层期权现金流受到复合参变量共同作用，即受到企业人力资本内在价值期权层进的叠套方向与叠套力度的决定，前者映射至企业人力资本内在期权价值现金流的增减趋势，而后者映射至人力资本价值的期权变动程度，两者交积则构成企业人力资本期权价值由层级叠套向定向跳跃的迈进，并预先为这种跳跃设定一个随机参变量λt；而当人力资本期权价值外部干扰因素不足以影响当期人力资本期权现金流时，对其对应更多当层期权现金流设定为基期无风险实物期权折算。

对应的可获得预定目标效应的人力资本期权投资成本现值可以被刻画成基于前述随机参变量，以及分段分布特征函数：

其次，针对上述折算过程进行由层级叠套向定向跳跃的发生频度、程度折算，此时，需设定一个动态参变量变动的到达界定参数λ，即判定企业人力资本期权价值现金流层级叠套是否达到跳跃的程度，λ为前述式中的泊松随机参数，由此可获得上述具备叠套特征的企业人力资本内在价值经过多次循环叠套的累积跳跃dn的随机部分，根据对于叠套行为的分析，研究设定φt为人力资本期权与现值的比例，当且仅当层进叠套指示信号为零时，不存在单一层次的人力资本叠套或跳跃行为，那么此时的企业人力资本内在期货现金流价值可被表述为：

式（13）中，φt这一动态参变量表示各层级企业人力资本内在期货价值彼此独立，并设定其初始值为零；且企业人力资本期权价值现金流层级叠套达到跳跃的程度临界影响因素由 φt|Xt来刻画，其形成了幅度为φt的人力资本期权价值基于改进Black-Scholes模型层级的跳跃。

根据上述分析，φt|Xt服从于上述瑞利分布，φt|Xt这一随机二维向量的企业人力资本内在价值二分量具备独立同方差的正态分布的分段分布特征，研究可以根据式（9）至式（13）进一步获取对应企业人力资本内在价值期权动态叠套折算的函数特征指标，其方差和均值分别为：

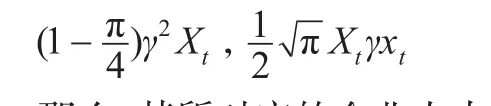
那么，其所对应的企业人力资本内在价值期权叠套折算模型可以归纳为：

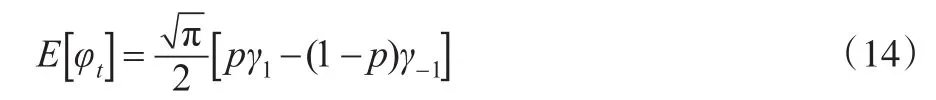
其中，γ1、γ-1和 p、1-p分别对应为人力资本作为期权价值发生现金流累积过程中的层级正负向性的跳跃及其发生跳跃行为的概率，式（10）在改进Black-Scholes模型下可被表述为：

这里研究主要将前述关于人力资本期权价值现金流累积方式的层级叠套折算跳跃行为的临界风险加以细化分析，即任何在层级叠套过程中发生的期权现金流跳跃也存在一定的风险，而并非简单的无风险假设，从而以式（15）中的零均值的维纳过程加以解释，该过程的正态分布方差仍为dt。

3 企业人力资本内在价值期权估计实证验证

3.1 企业人力资本内在期权价值随机最优控制

根据上述分析，研究利用算例进行企业人力资本内在价值期权折算。具体过程如下：

首先，利用期权价格的随机最优控制作为区间问题进行折算。设定人力资本以金融期权形式累积过程的上下限分别为V+(S，t)、V-(S，t)，借助区间控制函数u(t)=r(t)形成针对前述式（10）、式（15）改进的叠套层进跳跃行为期权现金流累积状态方程：

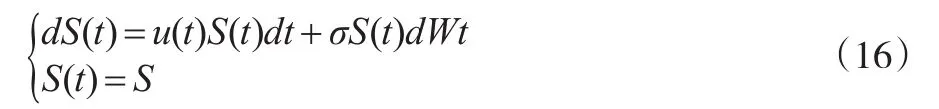
其中区间控制函数的控制集为：

该控制集必须确保在叠套层级幅度中全区可测，即具备一个全区可测集：

结合式（10）、式（14）构成基于人力资本内在期权价值指标关系的性能指标泛函数：

将人力资本内在期权价值叠套层级跳跃行为归纳为对于包含区间跳跃最优上下限控制集和最优控制函数uˉ(·)的测度模型：

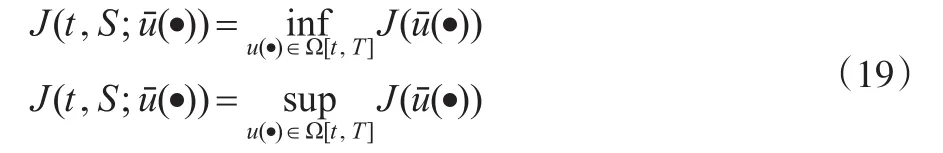
3.2 基于改进Black-Scholes模型的企业人力资本内在期权复合评价

根据上述分析，以叠套层级进行人力资本在企业内部期权属性变迁的区间划分，其对应的实际区间为招聘甄选期t0、进企直至被录用期t1、在职培训期T0

结合前述分析，将这一具备叠套层级跳跃的人力资本内在期权折算简化为：

上述各叠套跳跃期间的期望值为：

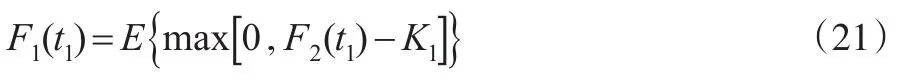
E作为期望算子，服从条件：

最后，针对人员在招聘甄选期、进企直至被录用期、在职培训期设定全区的人力资本期权现金流综合成本决策行为为第t0期，由此可获得具体叠套层级区间的点状人力资本内在期权价格折线为：

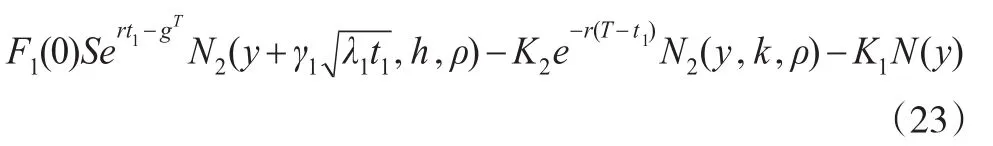
3.3 算例验证

某市高新区内生物技术公司，企业配备齐全的工种，并且具备独立人力资源部门。研究通过对该企业技术类型员工的样本选取，并依据该企业自2011—2014年的员工业绩考核数据，进行业绩加权平均，获得如表2所示的该企业人力资本工作绩效评估。

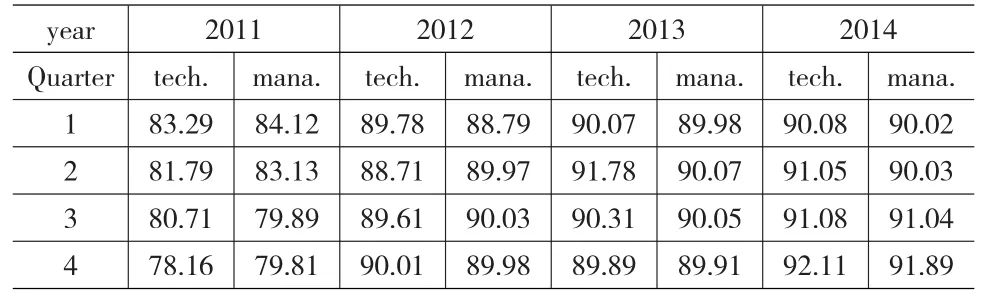
表2 企业人力资本内在价值样本分类业绩评估

接着，研究细化企业人力资本内在价值期权测度，并在结合2011—2014年对应员工工作业绩折算4年员工业绩加权平均值的基础上，进行期权资本价值波动率的折算，具体折算结果如表3所示。

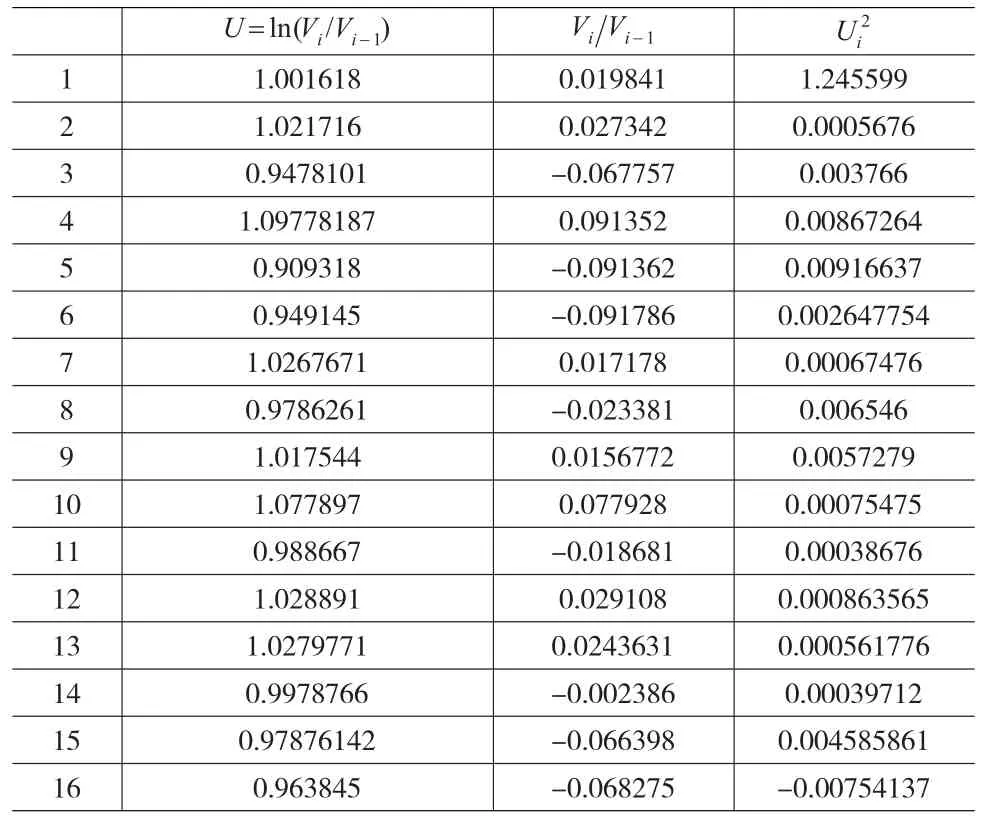
表3 人力资本业绩加权评级基础上的期权资本价值波动率折算

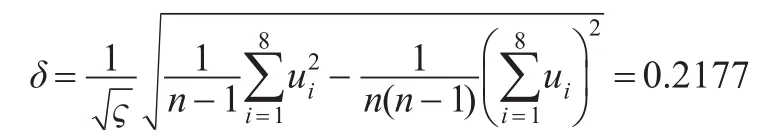
其中ς为样本观测值倒数的时间间隔。

该企业针对员工的福利主要由以下几部分构成：

每年人员招聘广告费用为5万元人民币，住房津贴共计9万元，人员工资支付为7万元每年，对应培训费为4万元每年，r=0.1，t=3，则结合式（5）、式（13）可获得叠套层级投资综合成本为：

同时，根据前述分析技术类负责经营层人力资本的收益为可以表述为：

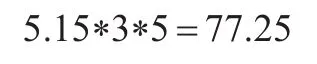
则在结合式（16）基础上，推算人力资本收益各跳跃期期权的微分现值为：

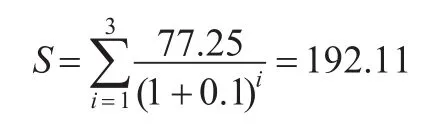
根据前述则可获得最终基于改进Black-Scholes模型的各项数值为S=192.11，X=110.98，δ=21.77%，经式（7）计算可得：

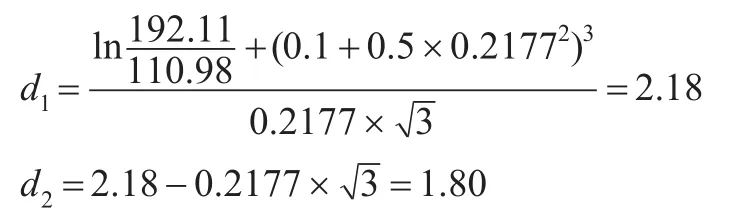
从算例验证结果来看，存在叠套和跳跃的超过了包含津贴、工资以及内部培训费用在内的20万元，因此经过改进Black-Scholes模型测算，可以获知这一类型的人力资本投入对于企业期权性质的投资具有持续意义。

4 总结

研究在结合当前企业人力资本内在价值评估研究的基础上，根据企业人力资本流动特征，以改进Black-Scholes模型的方法进行了针对于叠套行为特征的人力资本期权价值跳跃层级变动的评估研究。从人员招聘及甄选、内部培训等角度构建综合成本，并按照跳跃行为的临界判断作为企业人力资本期权价值累积的基础，进行了相应的人力资本期权价值折算。验算结果表明，改进Black-Scholes模型对于具备期权现金流映射价值叠套跳跃特性的人力资本评估存在较好的解释能力，在企业存在更为显著的人力资源动态调整期间的期权价值预测中，需要结合综合投入成本进行相应的人力资本期权价值估计。

[1]Ekström E，Tysk J.The Black–Scholes Equation in Stochastic Vola⁃tility Models[J].Journal of Mathematical Analysis’s&Sapplications， 2010，(2).

[2]Jarrow R A，Protter P，Shimbo K.Asset Price Bubbles in Incomplete Markets[J].Mathematical Finance，2010，(2).

[3]Muthuraman K.A Moving Boundary Approach to American Option Pricing[J].Journal of Economic Dynamics&Control，2008，(11).

[4]王艳培，刘继春.多个资产期权的泡沫和Black-Scholes方程[J].厦门大学学报:自然科学版，2014，(6).

[5]李洋，杨舒雅.最优资本结构选择与例证——基于权衡理论与Black-Scholes期权定价模型[J].财会通讯，2015，(1).

[6]任智格，何朗，黄樟灿.一种无风险利率时变条件下的Black-Scho⁃les期权定价模型[J].数学杂志，2015，(1).

[7]吕喜明，韩燕.基于MATLAB的Black-Scholes-Merton欧式期权定价模型的计算研究[J].经济论坛，2013，(6).

[8]景珮，李秀芳.我国财产保险公司资本结构的影响因素分析——基于权衡理论视角的实证检验[J].现代财经：天津财经大学学报， 2013，(1).

（责任编辑/浩 天）

C976.8

A

1002-6487（2016）21-0178-04

四川石油天然气发展研究中心基金项目（石油企业人力资本价值链研究）（川油气科SKW14-01）

廖特明（1970—），男，四川邻水人，硕士，副教授，研究方向:人力资源管理。

谭志勇（1982—），男，湖北咸宁人，博士研究生，研究方向：人力资源管理