考虑攻角的动能杆条对TBM目标穿甲模型研究*

韩晓明,朱 枫,陈俊杰

(空军工程大学防空反导学院,西安 710051)



考虑攻角的动能杆条对TBM目标穿甲模型研究*

韩晓明,朱 枫,陈俊杰

(空军工程大学防空反导学院,西安 710051)

为改进原来杆条斜穿甲方程的缺陷与不足,正确反映实际情况中杆条剩余速度、剩余质量与攻角、着角之间的关系。根据战术弹道导弹的目标特点,从动能杆条的终点穿甲机理出发,在参考原始弹道研究的破片穿甲方程和动能杆条正穿甲方程以及修正的杆条斜穿甲方程基础上,构造了模型简化过程,建立了新的修正的动能杆条斜穿甲带攻角穿甲计算模型。通过数值仿真,得到了杆条剩余速度、剩余质量与攻角、着角之间的变化规律,并且数值模拟结果与文献试验结果较为吻合,验证了模型的准确性。说明了新建立的穿甲模型的正确性,其更适用于实际情况。

动能杆;穿甲;计算模型;攻角

0 引言

战术弹道导弹TBM(tactical ballistic missile)是战区级火力支援的重要手段[1],由于其具有速度快、弹头坚固、雷达反射面积小、识别困难、突防能力强、命中精度高、不易被拦截等特点而成了最难对付的一类目标[2]。动能杆战斗部作为一种有效的反导战斗部,具有一定的应用前景,研究其针对TBM的杀伤威力具有十分重要的意义。

杆条的终点毁伤效能的分析是研究动能杆杀伤威力关键方式之一,而动能杆的穿甲威力是表征杆条终点毁伤效能的极为重要的一个方面,因此建立正确的动能杆穿甲威力模型对评估动能杆杀伤威力有着至关重要的作用。相比传统的破片或长杆穿甲过程,动能杆反导的终点毁伤杀伤元素具有大长径比、高着

靶速度、高质量、大着角和大攻角等特点。因此,文中主要从动能杆的终点穿甲机理出发,针对动能杆条的杀伤特点,通过理论分析,综合考虑多种影响穿甲效果的主要因素,建立考虑两种主要参数——剩余速度和剩余质量的动能杆带攻角穿甲威力模型,并进行数值仿真,以验证模型的准确性。

1 破片穿甲THOR方程

BRL的THOR方程根据多种破片材料和形状的大量试验数据的统计拟合,用于预估装甲材料对破片侵彻的弹道阻力。其基本方程有3种,为破片剩余速度THOR方程、目标防护速度THOR方程和破片的剩余质量THOR方程,剩余速度和剩余质量的THOR方程为[3]:

(1)

式中:Vr表示破片剩余速度(m/s);VR表示破片打击速度(m/s);h表示靶板材料厚度(m);A表示破片与靶板接触面积(m2);m0表示破片初始质量(kg);mr表示破片的剩余质量(kg);θR为杆条的夹角(°);c11～c35表示THOR方程中靶板材料参数,具体数值见表1[4]。

破片着角θR与靶板之间的关系如图1所示(其中VR方向为破片方向,靶板竖直放立)。

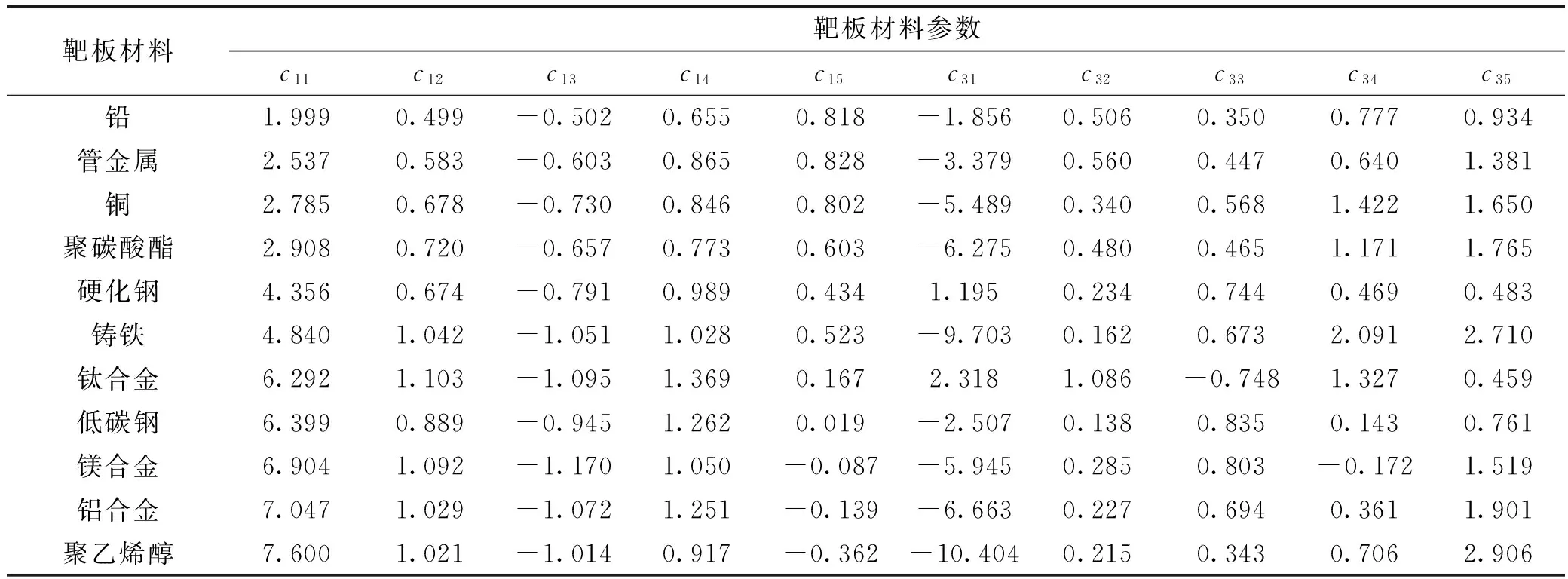
表1 THOR方程计算参数

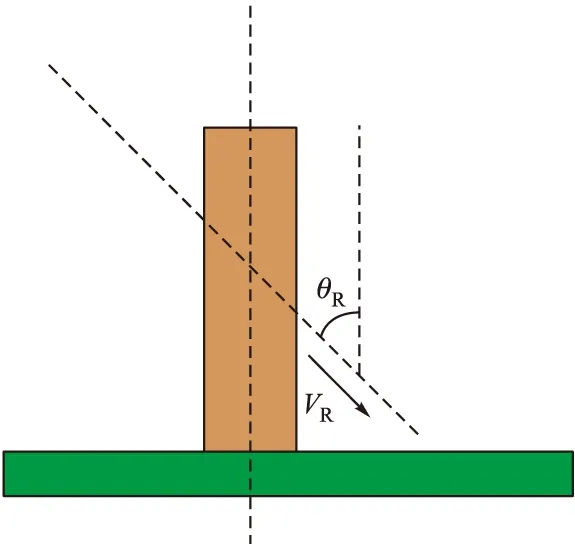
图1 着角θR与靶板之间

2 杆条穿甲THOR方程

杆条穿甲主要分为无攻角的正穿甲和有攻角的斜穿甲。杆条的正穿甲是指杆条与目标面接触时,速度的方向与杆条轴心的方向平行时的穿甲过程;杆条的斜穿甲是指杆条与目标面接触时,速度的方向与杆条轴心的方向具有一定夹角βR(即攻角)的穿甲过程[5]。杆条正穿甲和斜穿甲对比分析如图2。

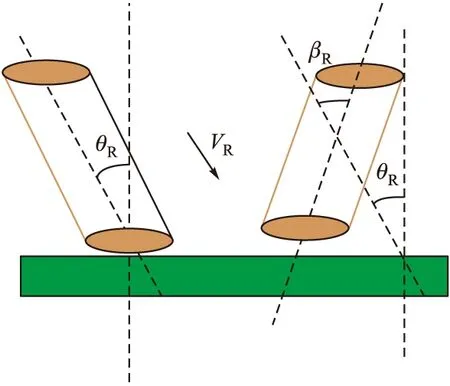
图2 杆条正穿甲和斜穿甲对比分析

2.1 动能杆条正穿甲(无攻角)的THOR计算模型

由于运用THOR方程计算时,需具备一个前提条件,即破片长径比不得超过3,且在此范围内的破片质量损失较大[3],所以导致通过利用长杆正侵彻的THOR方程的计算所得的剩余质量与试验数据相差较大。

因此THOR方程并不适用于计算长径比超过3的杆条的剩余质量,然而剩余速度将不受影响。考虑靶板厚度、靶板及杆条的材料波速等主要因素对杆条的极限质量损失的影响,修正破片穿甲THOR方程,得到杆条的正穿甲THOR方程[3]:

(2)

2.2 动能杆条斜穿甲(带攻角)的THOR计算模型

原BRL的THOR方程在预估剩余速度和剩余质量时只考虑了破片的初速、着角、质量以及靶板厚度、撞击面积等5个影响因素,没有考虑攻角的影响,或者说只考虑了攻角为0时的理想状态的情况。而动能杆战斗部作为新型的反TBM战斗部,具有较高的初速度和大着角、大攻角等终点毁伤特点,因此实际应用中必须考虑到攻角βR的影响,而攻角与着角对剩余速度的影响具有相似性。文献[6]考虑攻角的影响因素,将THOR方程局部修正为:

Vr=VR-0.304 8×10c11(61 023.7hA)c12(15 432.1m0)c13(secθ)c14(3.280 84V0)c15(secβR)k

(3)

然而系数k不给定,无法准确的得出攻角对剩余速度的影响,因此将攻角定向转化为穿靶截面积,模型简化过程如图3。

杆条是一个圆柱体,若将杆条段看成一整体等效长方形杆条穿靶[7],则等效靶板碰撞面积与实际情况存在一定的误差。因此将动能杆条看成等效的椭圆柱体杆条穿靶,不考虑等效杆条与原始杆条穿甲的宽度差异,且在长度上考虑两者的穿孔尺寸相等,将带攻角的杆条的复杂穿甲过程简化为等效截面积穿靶模型;杆条侵彻靶板过程中,在杆条与靶板之间找出与攻角βR有关的三角形ΔABC,求出与靶板横截面积相关的数据;将攻角与穿靶横截面积进行定量转换;得到的穿靶横截面积是两个半椭圆的面积与一个矩形面积之和,所得面积与文献[7]相比更为精确。

则建立新的修正的杆条带攻角的剩余速度THOR方程为:

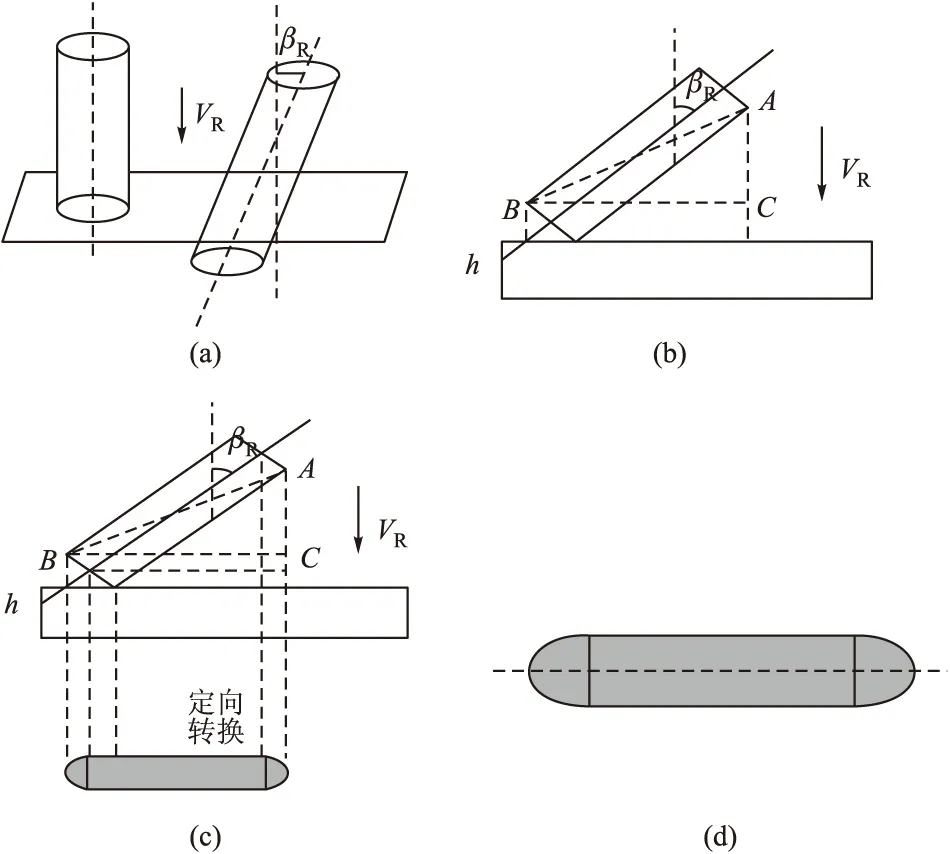
图3 动能杆攻角定向转化为穿靶截面积

(4)

式中:A′为动能杆转换后的碰撞截面积(m2);l为杆条的长度(m);r为杆条的底面半径(m);d为杆条的底面直径(m);βR为攻角。

建立新的修正的杆条带攻角的剩余质量THOR方程为:

(5)

则最终的修正的杆条带攻角的THOR方程为:

(6)

此为考虑攻角的动能杆条对TBM目标的最终穿甲模型。

3 计算与仿真

为分析杆条的剩余速度、剩余质量与攻角、着角之间的关系,并验证方程的准确性,根据文献[8]的预设侵彻条件,根据推导所得的最终修正的杆条带攻角THOR方程,利用Matlab仿真软件对杆条在靶板厚度为0.01 m和0.02 m时杆条带攻角情况下的剩余速度和剩余质量的变化情况进行数值仿真。

1)剩余速度与攻角之间关系的数值与仿真

根据相关数据[9],在杆条初速度为2 000 m/s时,分别对侵彻靶板的厚度为0.01 m和0.02 m时的剩余速度进行仿真,求得在攻角为10°、20°、30°、45°、55°、60°、90°,着角在0°～90°时的杆条剩余速度,如图4。并对根据修正后的THOR方程求得剩余速度与攻角的关系与相关数据[8]进行对比,如图5。

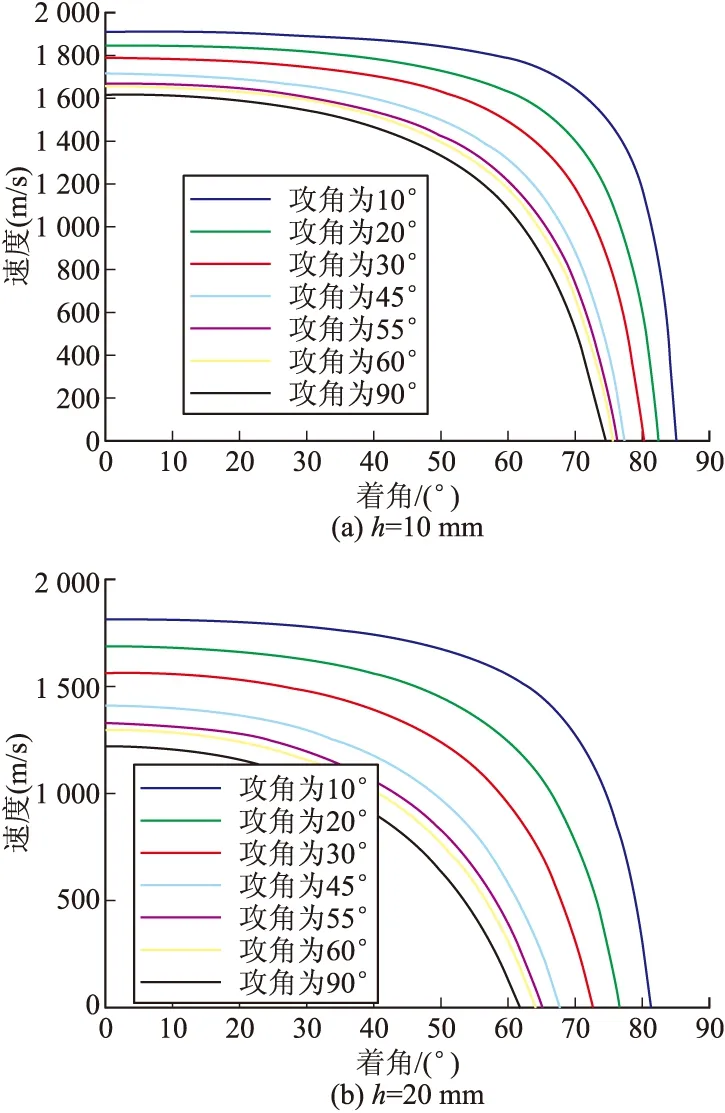
图4 杆条的剩余速度与杆条的着角的关系

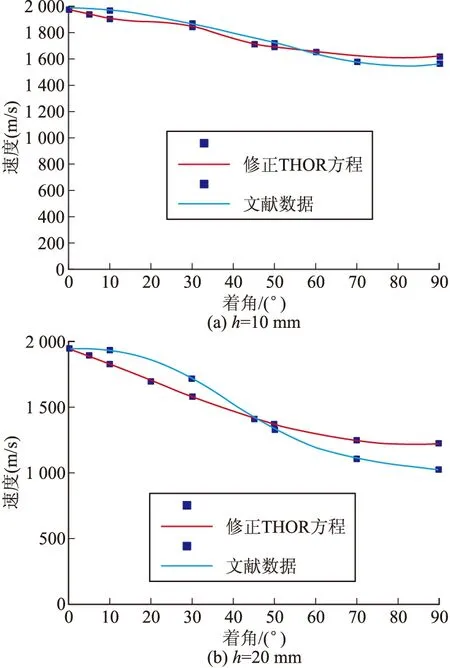
图5 修正方程与文献数据对比关系

2)剩余质量与攻角之间关系的数值与仿真

根据相关数据[8],在杆条初质量为0.62 kg时,分别对侵彻靶板的厚度为0.01 m和0.02 m时的相对剩余质量(百分比)进行仿真,求得在攻角为10°、20°、30°、45°、55°、60°、90°,着角在0°～90°时的杆条相对剩余质量(百分比)如图6。并对根据修正后的THOR方程所求相对剩余质量与攻角的关系与相关数据[8]进行对比,如图7。

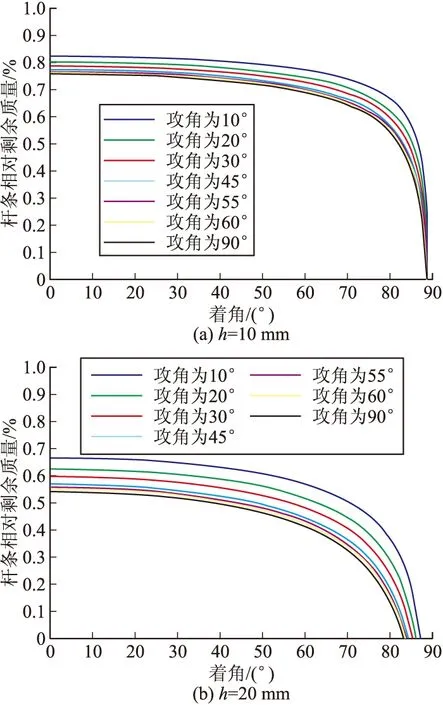
图6 杆条的相对剩余质量与杆条的着角的关系

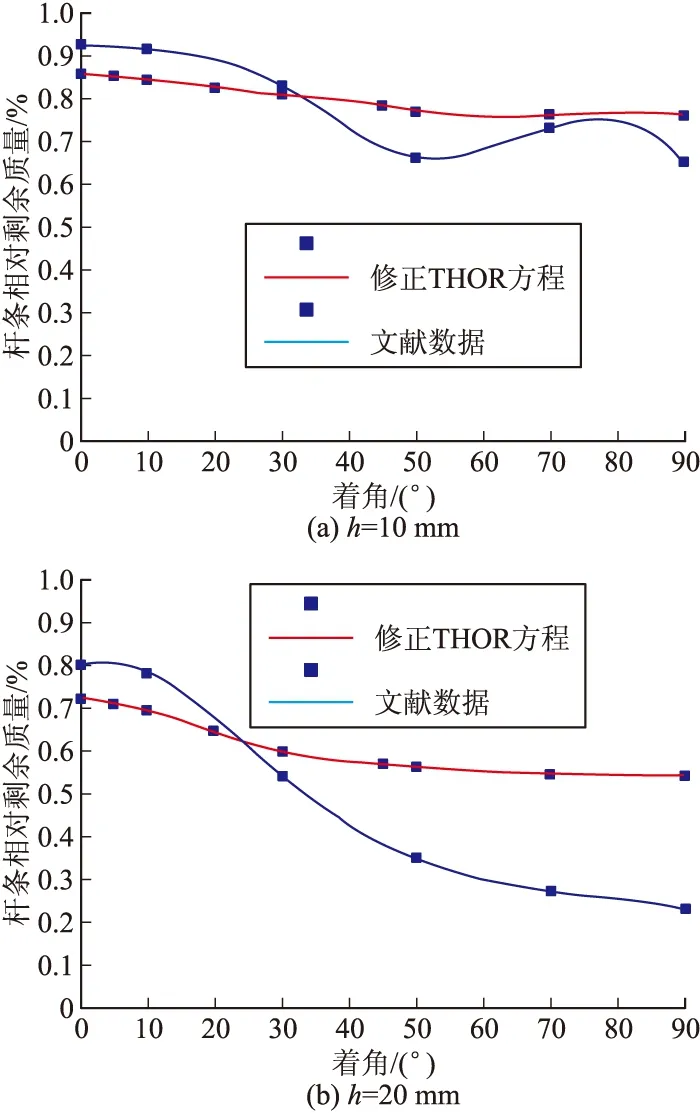
图7 修正方程与文献数据对比关系

3)结果分析

图4和图6分别反映了杆条在一定攻角情况下,穿靶后剩余速度和剩余质量与着角之间的变化规律,可以看出杆条穿靶后的剩余速度和剩余质量随着角的增大而减小,着角在0°～70°之间,杆条剩余速度的变化并不是很明显,当着角大于70°后,剩余速度明显下降,符合超出该区间可认为是无效破片(跳飞)的理论。

图5和图7分别反映了穿靶后剩余速度和剩余质量与攻角之间的变化规律,可以看出杆条穿靶后的剩余速度和剩余质量随攻角的增大而增大,在达到一个峰值后,又随着攻角的增大而减小,杆条在40°～45°之间变化最大,情况与参考数据(文献[8])较为吻合。

数值模拟结果与参考数据(文献[8])进行对比后可以看出,攻角对杆条穿甲后的剩余速度和剩余质量相比着角影响较大。因此,该计算模型能够更为准确客观地反映杆条攻角的影响趋势,效果明显,验证了方程的准确性,具有一定的适用性。

4 结论

文中在原始BRL的破片穿甲THOR方程基础上,同时参考动能杆条正穿甲THOR方程和修正的杆条斜穿甲THOR方程,针对杆条类杀伤元素对目标的终点毁伤特点,建立了更适用于实际情况新的修正的动能杆条斜穿甲带攻角THOR穿甲计算模型。在杆条斜穿甲计算模型建立过程中,将攻角定量转化为穿靶截面积,并使得到的面积更为精确。通过Matlab数值仿真,得到了杆条剩余速度、剩余质量与攻角、着角之间的变化规律,并且数值模拟结果与文献试验结果较为吻合,验证了模型的准确性。因此,建立的模型能较准确全面地分析动能杆战斗部在实际情况中的穿甲威力,具有一定的实用意义,为研究杆条对目标的终点毁伤效能和对TBM的杀伤威力奠定了基础。

[1] 廖新华. 美俄反导末段拦截技术之异同 [J]. 空军装备, 2008(6): 56-59.

[2] 刘庆鸿, 陈德源, 王子才. 动能拦截器拦截战术弹道导弹的脱靶量仿真 [J]. 系统仿真学报, 2002, 2(2): 200-203.

[3] 卢永刚. 基于THOR方程的杆条复杂姿态穿甲分析模型 [J]. 弹箭与制导学报, 2005, 25(1): 27-30.

[4] 李向东, 杜忠华. 目标易损性 [M]. 北京: 北京理工大学出版社, 2013: 180-191.

[5] 陈俊杰. 反TBM新型导弹战斗部毁伤效能综合评估 [D]. 西安: 空军工程大学, 2013.

[6] TAYLOR P A. Al/PTFE reactivematerial (RM24) sandia effort: experiment and modeling: SAND 2003 21840 P [R]. 2003.

[7] 卢永刚. 基于虚拟模型的动能杆反导战斗部毁伤效率评估方法: GF-A0090556G [R]. 中国工程物理研究院总体工程研究, 2004.

[8] 卢永刚. 动能杆对靶板毁伤效应的数值模拟研究: GF-A0090557G [R]. 中国工程物理研究院总体工程研究, 2004.

[9] DIEDEREN A M, Replica scale modeling og long rod tank penetratore [C]∥Switzerland, 19th International symposium on ballistics Interlaken, 7-11 May, 2001.

Model Research of KE-rod Piercing Armor Anti-TBM Considering Attack Angle

HAN Xiaoming,ZHU Feng,CHEN Junjie

(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

In order to improve earlier KE-rod slanting THOR armor-piercing model and correctly reflect relationships, based on the ending point armor-piercing mechanism and the characteristic of TBM, a new corrected KE-rod slanting THOR armor-piercing calculating model with angle of attack was built based on original BRL pieces armor-piercing THOR equation and KE-rod THOR armor-piercing model and KE-rod slanting THOR armor-piercing model. According to simulation, changing law for residual velocity, residual quality of rod and angle of attack, angle of entry was got, and veracity was checked by comparing simulation with testing result. It shows validity of the new model which is more suitable for actual situation.

KE-rod; armor-piercing; calculating model; angle of attack

2015-06-28

韩晓明(1961-),男,陕西渭南人,教授,博士,研究方向:装备管理理论与方法。

TJ 414.+2

A