一种弹载嵌入式软件数学模型测试方法的设计与实现*
刘 飞,蒲海峰,李柯达,谢菁珠,李 平,任文真
(中国兵器工业第203研究所,西安 710065)
一种弹载嵌入式软件数学模型测试方法的设计与实现*
刘 飞,蒲海峰,李柯达,谢菁珠,李 平,任文真
(中国兵器工业第203研究所,西安 710065)
为解决弹载嵌入式软件中数学模型测试存在输入不可控、通用性低等问题,文中基于弹载嵌入式软件中数学模型的独立性提出了一种新的测试方法。首先,提取数学模型代码,开发驱动程序和桩程序来实现数据的输入;其次,依据数学模型相关文档,利用Matlab进行模型搭建;最后,将提取出的数学模型代码的输出与Matlab搭建的模型输出进行对比,得到测试结果。在实际测试中,测试结果准确,表明该方法具有有效性和通用性。
弹载嵌入式软件;数学模型;软件测试
0 引言
由于导弹系统日益复杂,弹载嵌入式软件的复杂度也在不断提高,重要性也越来越高。导弹系统的组成如图1所示。其中,弹载计算机、导航装置以及导引头等弹上部件的嵌入式软件中包含有数学模型。作为弹载嵌入式软件的核心部分,数学模型也越来越复杂,其正确性直接决定了导弹系统的可靠运行。对数学模型正确性的测试是十分必要的。
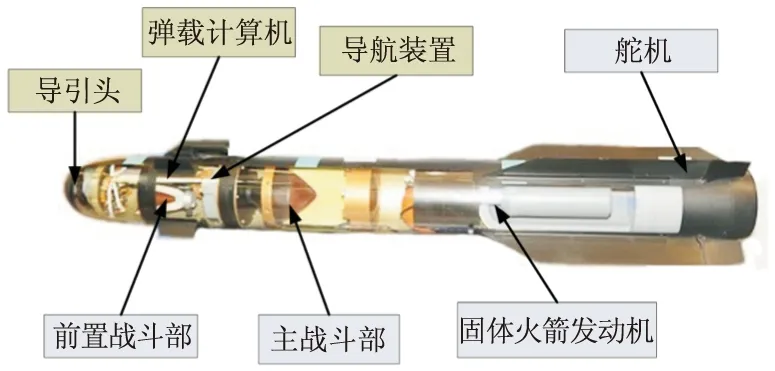
图1 美国AGM-114R导弹结构示意图
目前,对弹载嵌入式软件数学模型的测试没有通用并且有效的方法,主要是通过半实物仿真进行验证。在半实物仿真中,数学模型的输入来自导弹其他部件的输出,所以无法对数学模型的输入进行有效的控制。在软件测试中,测试用例的输入需要严格控制,才能保证测试质量。基于此,半实物仿真只能对导弹系统整体进行近似验证,无法精确验证数学模型正确性。半实物仿真中无法直接给数学模型进行数据输入,导致输入不可控,测试不充分。
针对以上问题,并基于弹载嵌入式软件代码中数学模型相对独立的特点,文中提出了一种新的测试方法。该方法通过对输入的有效控制,充分测试弹载嵌入式软件中数学模型的正确性,并通过两个实例来验证方法的有效性和通用性。
1 测试方法原理
完整的软件测试包括如下内容:设计测试用例、运行软件执行测试用例、判断测试用例是否通过测试。测试用例设计与具体数学模型功能相关,文中不展开论述。
在弹载嵌入式软件中,数学模型相关代码作为软件的一部分,不能单独运行并执行测试用例。但是由于在导弹系统中,数学模型代码主要负责数据处理和指令计算等核心功能,与硬件相关度低,且往往作为独立的模块存在于弹载嵌入式软件中。基于此,通过对数学模型代码进行提取、增加驱动函数和桩函数等技术手段,可以使其运行并执行测试用例,从而解决了输入不可控的问题。
执行测试用例后,输出数据需要与预期输出进行比对,决定测试用例是否通过测试。针对数学模型输入数据量大、运算复杂的特点,提出使用建模工具搭建数学模型获取预期输出的方案——将测试用例输入数据代入模型计算,即可获得预期输出。对比预期输出与实际输出,二者一致即说明通过验证。
2 测试方法设计
测试方法设计如图2所示。整个测试流程包含3个部分:1)提取数学模型代码;2)建模工具搭建数学模型;3)测试结果判定。
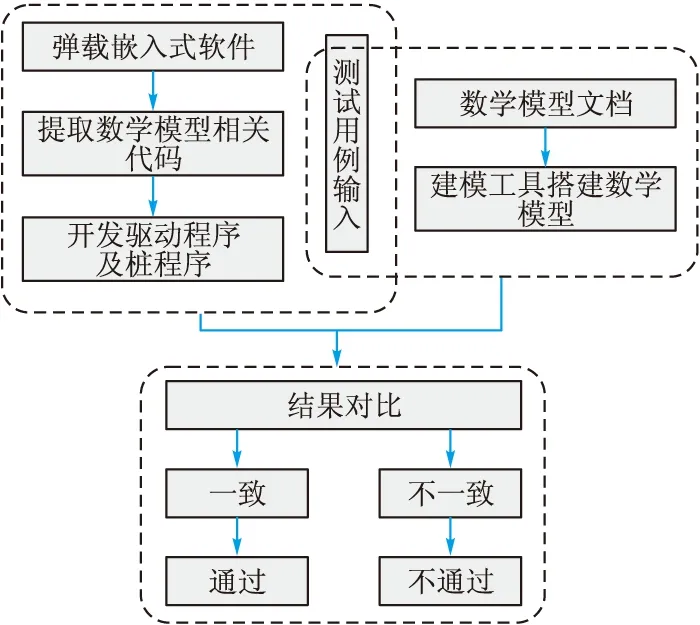
图2 测试流程图
2.1 提取数学模型代码
由于数学模型相关代码属于弹载嵌入式软件的一部分,不能独立运行,所以需要隔离数学模型代码单元,并根据数学模型相关代码的接口开发相应的驱动程序和桩程序。该过程是整个测试的首要步骤和关键内容。开发驱动程序与桩程序的过程,亦是弹载嵌入式软件数学模型相关代码提取过程的一部分。
驱动程序也称驱动模块,用以模拟被测模块的上级模块,能够调用被测模块。在测试过程中,驱动模块接收测试数据,调用被测模块并把相关的数据传送给被测模块。桩程序也称桩模块,用以模拟被测模块工作过程中所调用的下层模块,桩程序本身不执行任何功能,仅在被调用时返回静态值来模拟被调用底层模块的行为,替代所需调用的底层模块,使得整个程序能够顺利运行。通过驱动程序和桩程序隔离被测模块,使被测模块可以执行测试,如图3所示。驱动程序作为入口,可以设置不同的参数,执行各种测试用例。
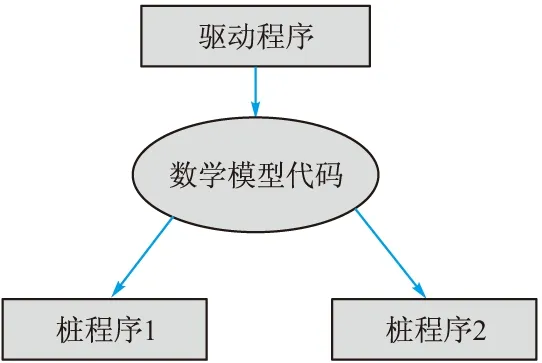
图3 驱动程序与桩程序
在弹载嵌入式软件数学模型测试中,需要开发人员提供或者由测试人员找出相应的程序接口,根据接口定义设计驱动程序和桩程序,通过对数学模型代码进行调用,即得到可执行的数学模型代码。
2.2 建模工具搭建数学模型
建模工具搭建数学模型的意义在于提供测试用例的预期输出,用以判定测试结果是否正确。文中使用Matlab进行数学模型搭建。
数学模型文档作为Matlab模型搭建的依据,必须与待测软件中数学模型相关代码的文档依据一致。该过程是判定测试结果是否正确的关键步骤,保证Matlab所搭建模型的正确性是至关重要的。
2.3 测试结果判定
通过提取出的数学模型代码执行测试用例,可以得到实际的运行结果;通过Matlab搭建的数学模型执行相同的测试用例,可以得到预期的运行结果。对比实际运行结果和预期运行结果,若两者一致,则该用例通过测试;若两者不一致,则该用例未通过测试,说明数学模型代码有缺陷。
3 实例验证
为验证文中设计的弹载嵌入式软件数学模型测试方法的有效性和通用性,对某导弹弹载计算机软件数学模型和某导弹惯性导航装置软件数学模型进行了测试。
3.1 弹载计算机软件数学模型测试
弹载计算机是导弹的核心部件之一。为了有效控制导弹飞行轨迹和姿态,弹载计算机需要从导引头、导航装置等部件获得实时数据以及目标和导弹的相对位置,经过数学模型计算,实时输出舵指令到舵机,进而控制导弹飞行。弹载计算机基本工作原理如图4。
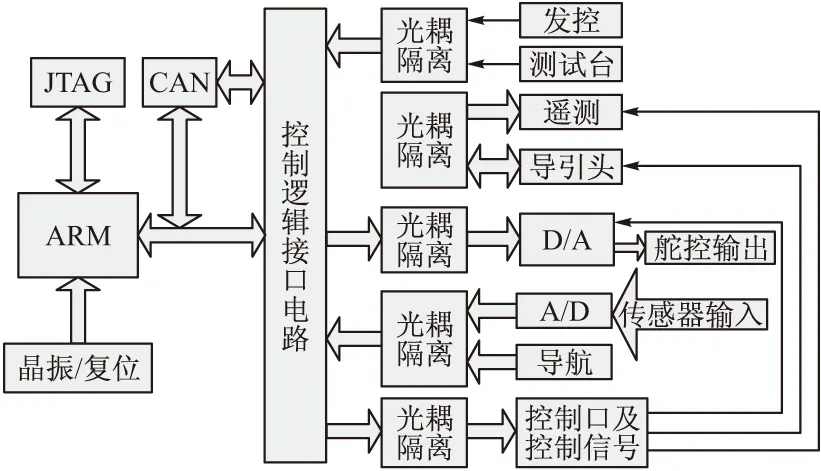
图4 弹载计算机基本工作原理
按照文中的测试方法,提取弹载计算机软件数学模型相关代码,开发驱动程序以及桩程序;同时;依据数学模型文档进行Matlab模型搭建。
假设目标为静止,目标信息、环境信息和导航信息等测试用例输入数据为:
目标、环境信息:
温度:20 ℃;
载机速度:45 m/s;
海拔高度:3 000 m;
目标X向初始位置:2 500 m;
目标X向位置:2 500 m;
目标Y向位置:0;
目标Z向位置:0;
导航信息:
导弹X向位置:200t;
导弹Y向位置:-(t-0)(t-50);
导弹Z向位置:-(t-0)(t-50);
导弹滚转角:5sin(πt/10);
导弹偏航角:5sin(πt/10);
导弹俯仰角:5sin(πt/10);
滚转角速度:2sin(2πt/5);
偏航角速度:2sin(2πt/5);
俯仰角速度:2sin(2πt/5);
导弹X向速度:-10/625×(t-0)(t-50);
导弹Y向速度:10sin(πt/10);
导弹Z向速度:10sin(πt/10)。
分别运行待测程序和Matlab模型,可以得出舵指令输出曲线,如图5所示:左侧为被测数学模型实际输出曲线,右侧为Matlab模型输出曲线。两组输出的舵指令之差数量级为10-4,满足弹载计算机软件数学模型解算的误差要求。
测试结果表明,弹载嵌入式软件数学模型代码实现与需求一致。
3.2 惯性导航装置软件数学模型测试
惯性导航装置由加速度计、陀螺仪等惯性测量元件和导航计算机组成。由加速度计测量导弹的加速度,陀螺仪测量导弹的角运动,并在给定运动初始条件下,经导航计算机数学模型转换、处理,计算出导弹的速度、距离和位置(经纬度)、姿态和航向信息,输出到弹载计算机。
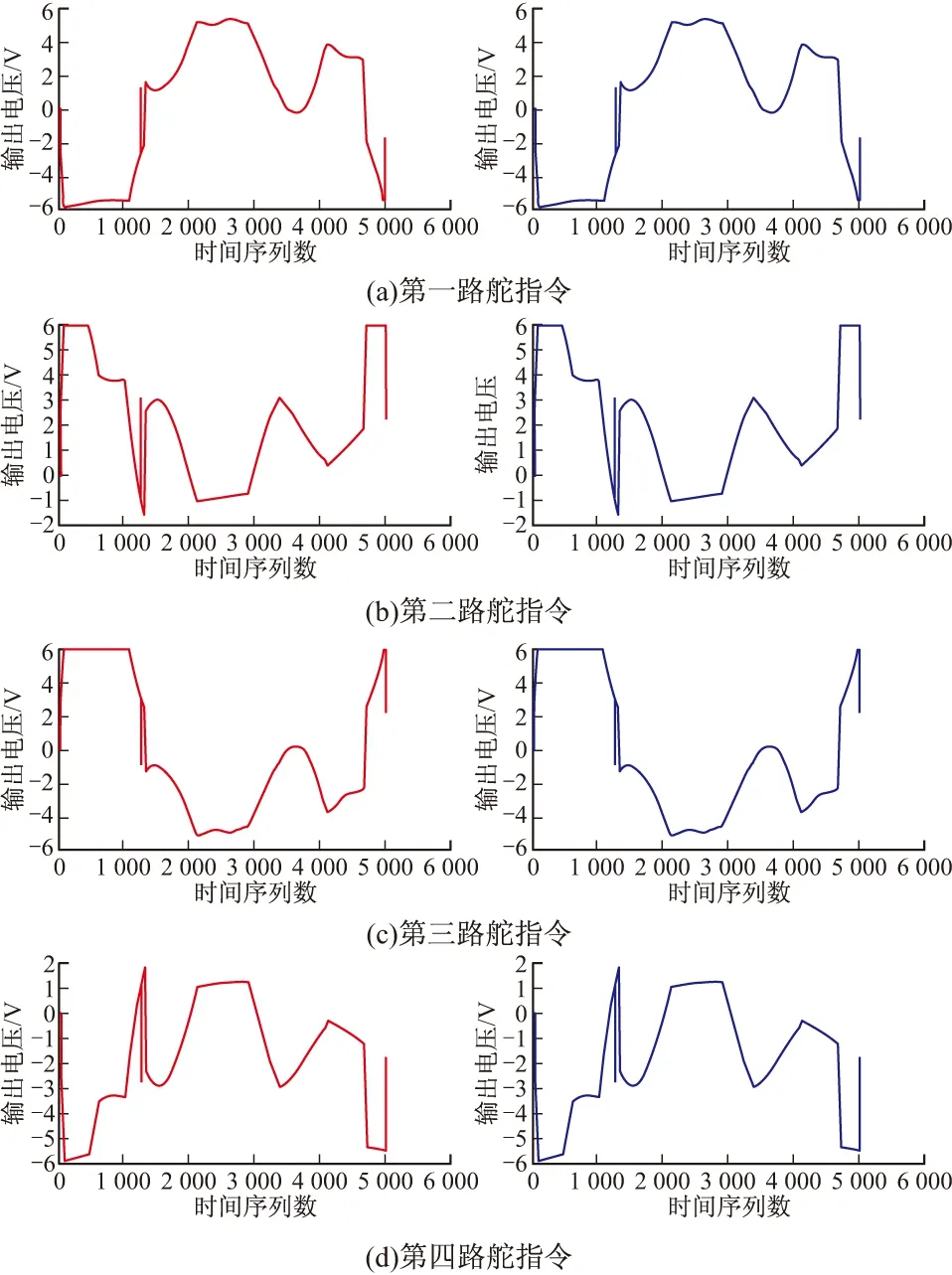
图5 舵指令对比图
同样,运用文中测试方法,对惯性导航装置软件数学模型进行测试。由于输出较多,文中只取导弹速度进行说明,如图6所示,依次为导弹在X、Y、Z方向的速度分量。
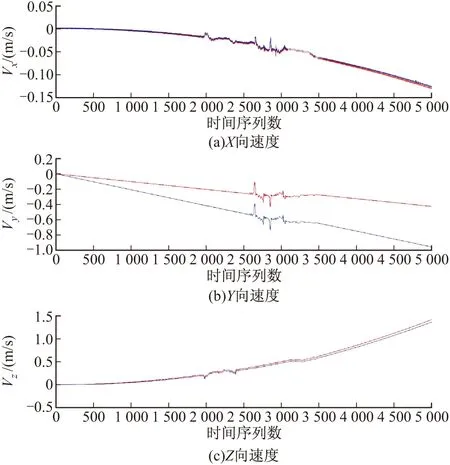
图6 导弹速度对比图
红色曲线为被测惯性导航装置软件数学模型实际输出,蓝色曲线为Matlab模型输出曲线。其中,X和Z方向的速度分量满足数学模型计算误差要求,Y方向速度分量不满足要求,即数学模型代码实现出现错误。经开发人员确认问题并修改代码后,Y方向速度分量满足要求。
4 结论
文中设计的测试方法成功解决了弹载嵌入式软件数学模型测试中输入不可控的问题,能够对数学模型进行较为充分的测试。同时,该方法在弹载计算机软件和惯性导航装置软件数学模型测试中的成功运用,证明该方法具有一定的通用性。在文中的基础上,如何针对弹载嵌入式软件数学模型进行有效的测试用例设计,以及Matlab模型搭建正确性验证等问题值得进一步研究。
[1] 徐仁佐. 软件可靠性工程 [M]. 北京: 清华大学出版社, 2007: 75-91.
[2] 高江林, 吴晓燕, 李勇君, 等. 半实物仿真系统VV&A研究 [J]. 航天控制, 2011, 29(1): 67-71.
[3] 朱少民. 软件测试方法和技术 [M]. 北京: 清华大学出版社, 2010: 107-108.
[4] 周伟明. 软件测试实践 [M]. 北京: 电子工业出版社, 2008: 158-160.
[5] 林晓欲, 石磊. 嵌入式软件系统测试模型的研究与实现 [J]. 科学技术与工程, 2009, 9(24): 7515-7520. .
[6] 王娟. 软硬结合的嵌入式软件在线测试系统 [D]. 成都: 电子科技大学, 2009.
[7] 毛伟云, 陈明, 丁力, 等. 嵌入式实时操作系统μC/OS-Ⅱ在弹载计算机上的应用 [J]. 弹箭与制导学报, 2007, 27(4): 349-356.
[8] 朱家海. 惯性导航 [M]. 北京: 国防工业出版社, 2008:2-3, 203-204.
Design and Implementation of a Mathematical Model Test Method for Missile-borne Embedded Software
LIU Fei,PU Haifeng,LI Keda,XIE Jingzhu,LI Ping,REN Wenzhen
(No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)
In order to solve several problems in mathematical model test of missile-borne embedded software,such as uncontrollable input and poor versatility, a new test method is proposed to solve the problems above in this paper. This method is based on the mathematical model’s independence of missile-borne embedded software, Firstly, extract the mathematical model code, and develop drive program and pile program to achieve the data input. Secondly, on the basis of the mathematical model related documents, Matlab is used to build model. Finally, by comparing the output of the extracted mathematical model with the model output of Matlab code, test results are got. In actual test, the results are accurate, which demonstrate that the method is efective and versatile.
missile-borne embedded software; mathematical model; software testing
刘飞(1988-),男,陕西延安人,硕士研究生,研究方向:软件工程。
TJ760.6
A
2015-12-28

