基于量纲分析法的EFP速度计算模型*

张 健,程 春,相升海,李 然,赵 爽,韩继龙

(1 沈阳理工大学装备工程学院,沈阳 110159;2 东北工业集团有限公司吉林江机公司,吉林吉林 132021)



基于量纲分析法的EFP速度计算模型*

张 健1,程 春1,相升海1,李 然2,赵 爽1,韩继龙1

(1 沈阳理工大学装备工程学院,沈阳 110159;2 东北工业集团有限公司吉林江机公司,吉林吉林 132021)

爆炸成型弹丸的速度是影响EFP战斗部侵彻能力的一个重要因素。基于量纲分析与数值计算相结合的方法建立了一种求解球缺罩EFP速度的计算模型,并对计算模型进行了算例分析。结果表明,该模型可以定量反映EFP速度与装药长度、药型罩内径、罩顶厚度之间的函数关系,其计算结果和算例的计算结果吻合较好,可以对球缺罩EFP战斗部的设计提供参考。

爆炸成型弹丸;量纲分析;计算模型

0 引言

爆炸成型弹丸(explosively formed projectile, EFP)战斗部是一种用于对付装甲目标的新型装药战斗部,随着智能弹药的发展,爆炸成型弹丸战斗部常被应用于末敏弹、智能雷、反坦克导弹等反装甲弹药[1]。EFP的速度是影响EFP战斗部侵彻能力的重要因素,研究EFP的速度与EFP战斗部结构的关系对于EFP战斗部的设计非常重要。周翔等提出了一种基于能量法则的EFP速度的工程计算方法[2];赵慧英等从炸药装药的瞬时爆轰产物飞散理论出发,结合能量守恒定律推导了EFP速度的计算模型[3]。

文中采用量纲分析法对球缺形紫铜EFP的速度与炸药参数以及药型罩参数的关系进行分析,得到EFP速度的量纲表达式,并结合正交设计法进行EFP速度的数值计算,推导出速度与炸药和药型罩结构尺寸关系的数学模型。

1 量纲表达式的建立

量纲分析法是一种不考虑自然现象或工程问题具体过程的寻求某种物理规律的方法,量纲分析法的基本原理是量纲齐次原理。量纲分析法的一般过程是:首先,把问题所涉及的物理量按属性进行分类,其次,需要找出不同类物理量之间具有什么样的相互联系,最后,进一步找出某些物理量与另外一些物理量之间的函数关系。量纲分析法的过程实质上是数学建模的过程,建模的原理是E.Buckingham在1914年提出的∏定理[4]。

图1是等壁厚球缺形药型罩EFP战斗部的模型示意图。影响这种EFP速度的参数主要有:装药长度Le,装药密度ρe,单位质量炸药的化学能Ee;药型罩内径rs,罩顶厚度ds,药型罩密度ρs。

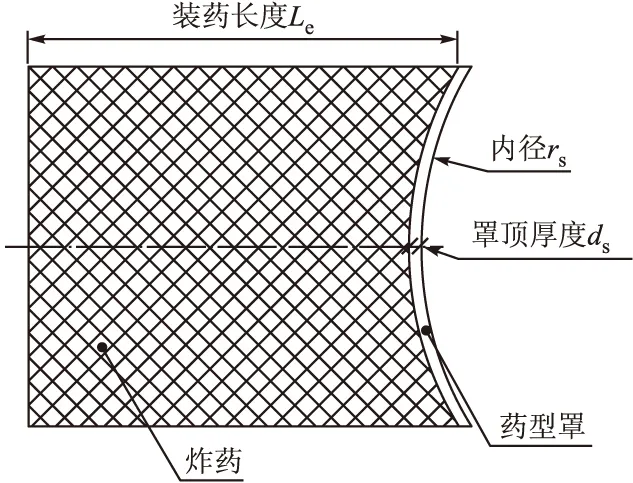
图1 EFP战斗部的模型示意图

取长度L,质量M,时间T为基本量纲,则上述物理量的量纲分别为:[Le]=L,[ρe]=ML-3,[Ee]=L2T-2,[rs]=L,[ds]=L,[ρs]=ML-3,EFP速度V的量纲[V]=LT-1。速度V与上述几个因素的函数关系可以通过分析和数据处理得到。令f(V,Le,ρe,Ee,rs,ds,ρs)=0。

得到量纲矩阵:

(1)

该量纲矩阵的秩为3,由参考文献[5]得:

方程AY=0有7-3=4个基本解其中Y=(y1,y2,y3,y4,y5,y6,y7)T。

令y1=1,y3=0,y5=0,y6=0;y1=0,y3=1,y5=0,y6=0;y1=0,y3=0,y5=1,y6=0;y1=0,y3=0,y5=0,y6=1;得到4个基本解,分别为:

(2)

根据量纲分析的∏定理,得到4个新的无量纲因变量:

(3)

且4个无量纲量存在一个函数关系:

F(Π1,Π2,Π3,Π4)=0

(4)

从而有函数关系:

Π1=φ(Π2,Π3,Π4)

(5)

把式(3)代入式(5)得:

(6)

于是得到速度V的量纲表达式:

(7)

式中函数φ的具体形式将利用数值计算的结果推导出来。

2 数值计算及其结果

数值计算采用有限元计算方法。建立四分之一材料模型,整个计算区域划分6 900个六面体单元,其中炸药部分6 000个单元,药型罩部分900个单元,药型罩和炸药之间采用单面滑移接触,采用后点单点起爆方式。数值计算中炸药为B炸药,选用高能炸药爆轰材料模型(High-Explosive-Burn)和JWL状态方程,药型罩材料采用紫铜,选用Steinberg材料模型和Gruneisen状态方程,炸药的材料性能参数,药型罩的主要参数数据见文献[6]。实物和计算模型见图2。

图2 实物照片和计算模型图

数值计算方案通过正交设计法确定。数值计算方案中炸药的密度、单位质量炸药的化学能和药型罩的密度不变,选择装药长度Le、药型罩内径rs、药型罩罩顶厚度ds三个因素;每个因素设置四个水平。数值计算方案和计算结果见表1。

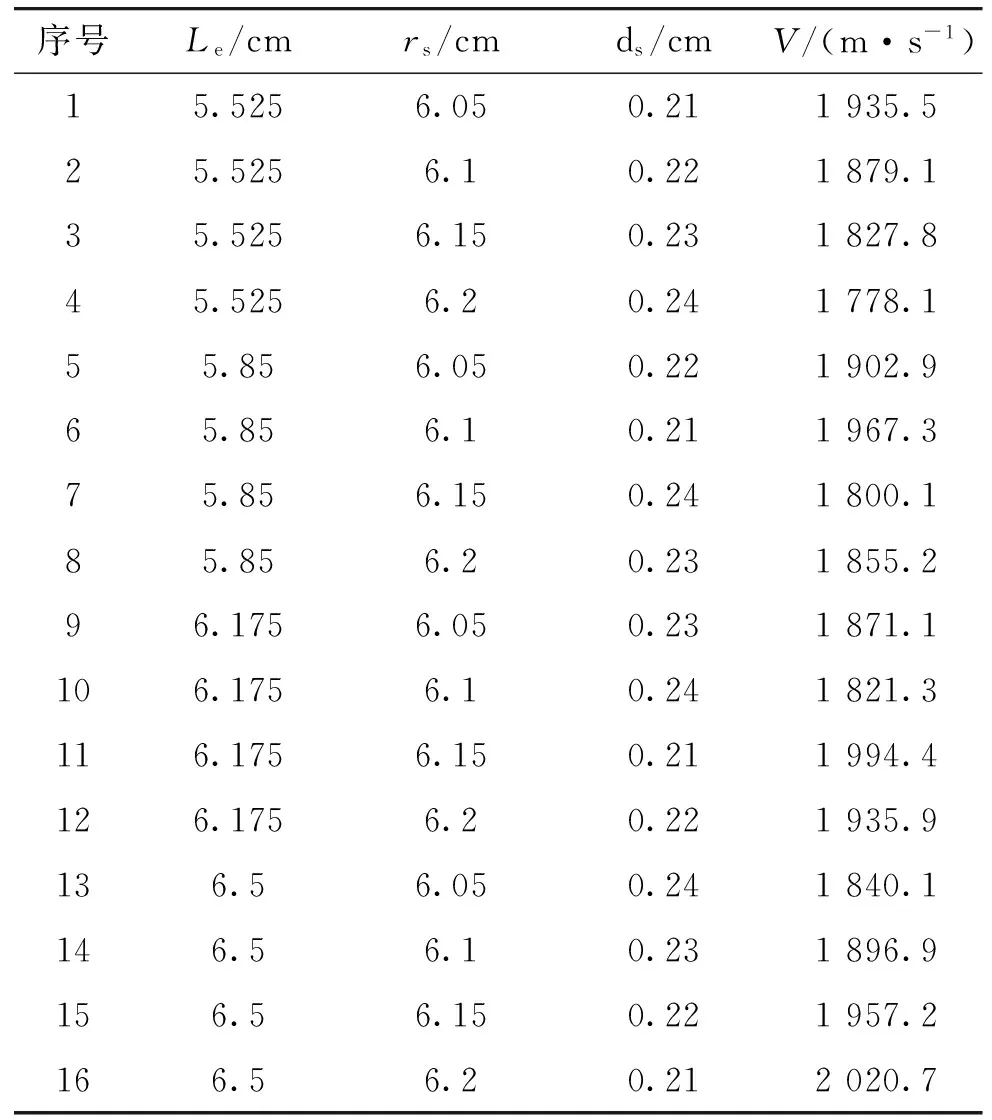
表1 数值计算方案和计算结果

3 基于量纲分析法与数值计算的速度计算模型

3.1 速度计算模型

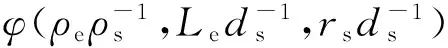
(8)

因为ρe、Ee、ρs三个量不变所以式(8)可以化简为:

(9)

进一步化简得:

(10)

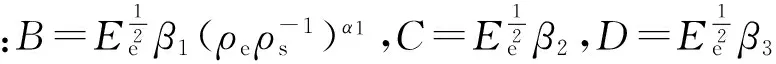
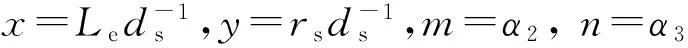
V=B+Cxm+Dyn

(11)

非线性曲面拟合是Origin9.0的特色功能之一,而且Origin9.0具有求解自定义函数的功能,因此采用Origin9.0进行曲面拟合得到待定字母的值。具体拟合过程见图3所示的自定义函数曲面拟合流程图。

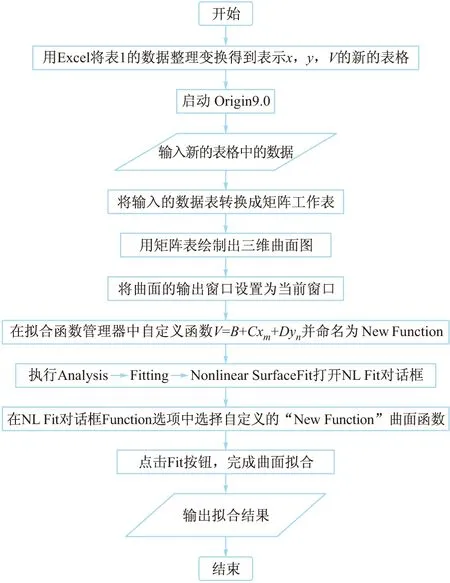
图3 自定义函数曲面拟合流程图

曲面拟合得到B=7.544,C=563.75,D=0.392,m=0.294,n=2.095,于是得到:

V=7.544+563.75x0.294+0.392y2.095

(12)

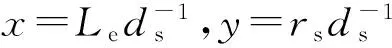
(13)

拟合出来的函数图像如图4所示。

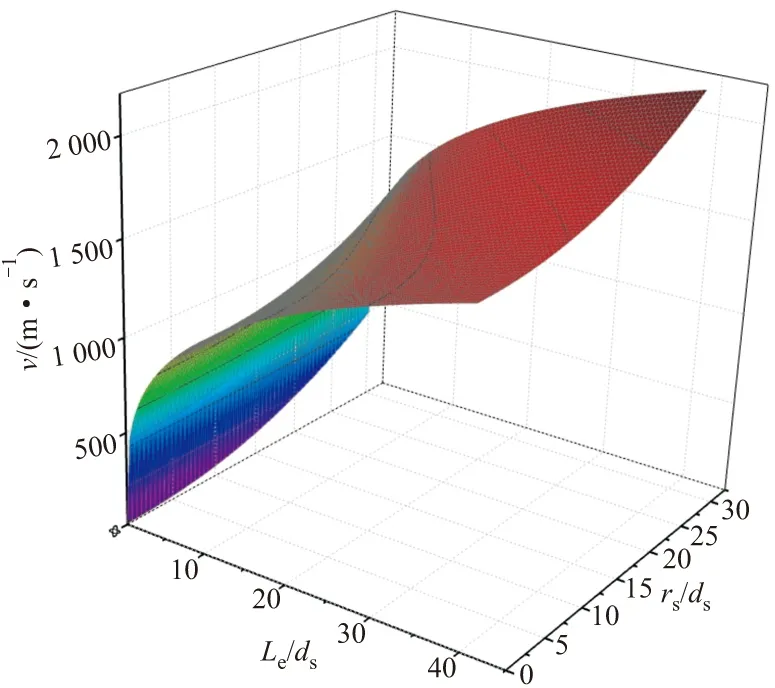
图4 拟合的函数图像

3.2 算例及其计算结果分析

在表1的数值计算方案之外分别取3组数据作为算例进行对比计算,第一组数据Le=5.525 cm,rs=6.05 cm,ds=0.3 cm,第二组数据Le=5.525 cm,rs=6.4 cm,ds=0.21 cm,第三组数据Le=4.225 cm,rs=6.05 cm,ds=0.21 cm。有限元法计算结果和计算模型计算结果的对比见表2。

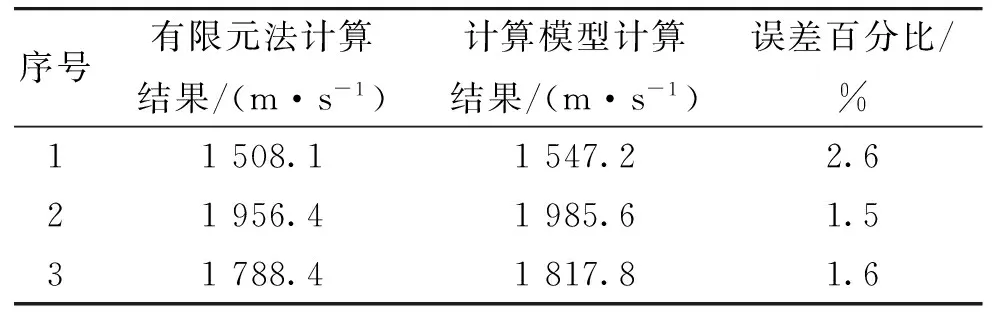
表2 有限元法计算结果和计算模型计算结果对比

最大误差为2.6%,证明了计算模型的可行性。

4 结论

1)提出了一种新的计算EFP速度的方法,并对计算模型进行了算例分析,表明该计算模型是可行的。

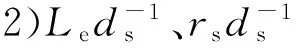
3)文中计算模型避免了对药型罩在爆轰波瞬时高压作用下的变形过程和机理的分析,可以对球缺形药型罩的设计提供参考。

[1] 彭庆明. 自锻破片战斗部设计方法的讨论 [C]∥第四届破甲会议文集. 西安: 中国兵工学会弹药分会, 1984: 41-50.

[2] 周翔, 龙源, 岳小兵. 等, 一种基于能量法则的爆炸成型弹丸速度的工程计算方法 [J]. 爆炸与冲击, 2005, 25(4): 378-381.

[3] 赵慧英, 沈兆武. 爆炸成型弹丸速度计算方法研究 [J]. 中国工程科学, 2007, 9(8): 62-65.

[4] 谈庆明. 量纲分析 [M]. 合肥: 中国科学技术大学出版社, 2005: 9-17.

[5] 付泽民, 莫健华, 陈伟, 等. 基于量纲分析法的金属板材折弯回弹数学模型 [J]. 机械工程学报, 2010, 46(12): 53-58.

[6] 刘建青, 郭涛, 顾文彬, 等. 三点起爆形成尾翼EFP的数值模拟和实验研究 [J]. 爆炸与冲击, 2013, 33(1): 38-46.

EFP Velocity Calculation Model Based on Dimensional Analysis Method

ZHANG Jian1,CHENG Chun1,XIANG Shenghai1,LI Ran2,ZHAO Shuang1,HAN Jilong1

(1 School of Equipment Engineering, Shenyang Ligong University, Shenyang 110159, China;2 Jilin Jiangji Company, Northeast Industries Group Co. Ltd, Jilin Jilin 132021, China)

Velocity of explosively formed projectile is an important factor that influences penetration capability of EFP warhead. For hemispherical liner, a calculation model of EFP speed was established according to combination of dimensional analysis and numerical calculation, and the calculation model was verified by calculation examples. The results show that the model quantitatively reflects the function relationship between the EFP velocity and the length of the charge, the inner diameter, the thickness of the cover. The results of the calculation model are in good agreement with the results of the calculation examples, the model guides design of hemi-spherical liner EFP warhead.

explosively formed projectile; dimensional analysis; calculation model

2015-06-24

张健(1961-),男,辽宁沈阳人,教授,博士,研究方向:弹药工程。

TJ410.3+3

A