两招制胜几何体与球的切、接问题
◇ 山东 孙墨涵
两招制胜几何体与球的切、接问题
◇ 山东 孙墨涵
柱、锥、台、球等简单几何体的结构特征,是立体几何的基础,它们的表面积与体积(尤其是体积)是每年高考热点,其中几何体与球的切、接问题出现频率较高.一般情况下旋转体中的圆锥、圆柱与球的切、接问题比较简单,在此不做赘述,本文重点研究多面体与球的切、接问题.
1 几何体与球的相接问题
例1 若长、宽、高分别为a、b、c的长方体的顶点都在同一球面上,求该球的直径2R.
过长方体的一个对角面作组合体的截面图,显然有
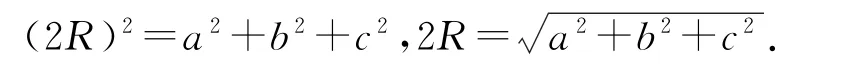
长(正)方体的外接球直径是长(正)方体的体对角线.
方法1 过正四面体的高AG所在直线和正四面体的一条侧棱AB作出组合体的截面如图1,找准球心位置,构造三角形求解半径.在Rt△ABG中,由勾股定理可求得在 Rt△ABE中,由射影定理可求得AE即直径2R=
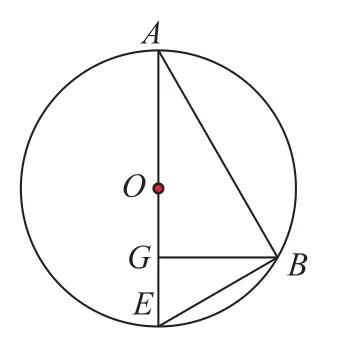
图1

图2
正四面体外接球的球心在高线上,半径是正四面体高的3/4.
两招制胜 几何体的外接球问题:一方面,可以考虑作组合体的合适的截面,在截面中找到球的半径和所给棱长的关系;另一方面,也可以考虑所给几何体是哪个常见几何体(长方体、正方体、棱柱)的切割后的图形.
2 几何体与球的相切问题
例3 求棱长为a的正四面体的内切球的半径.
由正四面体本身的对称性可知,内切球的球心就是正四面体的体心,连接体心和4个顶点,正四面体被分成4个全等的正三棱锥,正三棱锥和正四面体的底面积相同,体积是正四面体的1/4,所以高是正四面体高的1/4,所以球心为正四面体高的四等分点,即内切球的半径为h/4(h为正四面体的高),从而可以通过图3中正四面体的截面图如图4所示,在Rt△BEO中,BO2=BE2+EO2,即R2=因为R=3r,解得

图3

图4
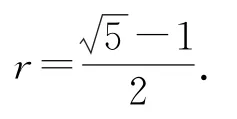
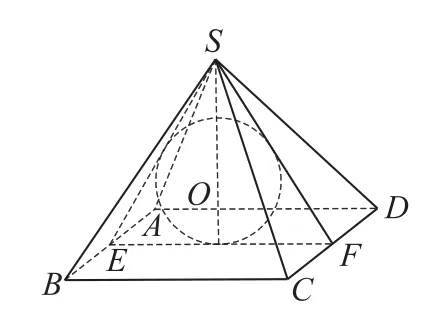
图5
方法2 连接球心与四棱锥的5个顶点,则四棱锥被分割为一个小四棱锥和四个等底的三棱锥,由等体积法可求得球的半径.
两招制胜 几何体与球相切问题:1)作组合体的合适的截面,在截面中根据线段关系解三角形或者用等面积法求解;2)因为球心到几何体的各个面的距离相等,都为球半径,所以求球的半径可转化为求球心到几何体各面的距离,直接用等体积法解决.
(作者单位:山东省莱芜市莱城区凤城高级中学)

