向量法在立体几何中的应用

◇ 江苏 袁军俊

向量法在立体几何中的应用

◇ 江苏 袁军俊

空间向量的引入为立体几何问题的求解提供了程序化的方法,其原理是利用向量坐标定义将空间关系转化为向量之间的关系.下面举例分析.

例 如图1,在Rt△ABC中,∠ACB＝30°,∠ABC＝90°,D为AC中点,AE⊥BD于E,延长AE交BC于F,将△ABD沿BD折起,使面ABD⊥面BCD,如图2所示.

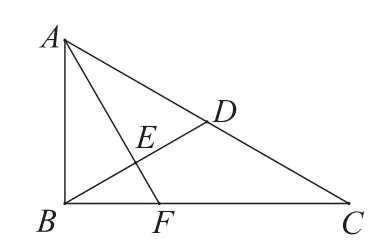
图1

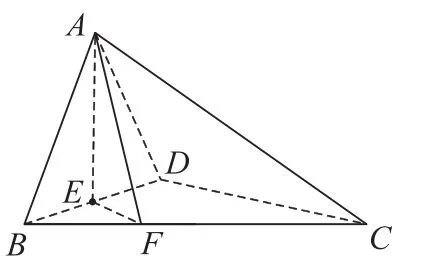
图2

(1)求证:BD⊥AF;

(2)求二面角A-DC-B的余弦值;

(3)在线段AF上是否存在点M使得EM∥平面ADC?若存在,请指明点M的位置;若不存在,请说明理由.

1 判断空间垂直关系

空间的垂直关系包括:线线垂直、线面垂直、面面垂直.其中:线线垂直的判定可通过判断2直线的方向向量数量积为0来实现;线面垂直可通过判断直线的方向向量与面内不共线的2向量垂直来实现;面面垂直可利用2平面的法向量垂直来判定.

第(1)问解答 因为平面ABD⊥平面BCD,交线为BD.又在△ABD中,AE⊥BD于E,AE⊂平面ABD,所以AE⊥平面BCD,AE⊥EF.由题意可知EF⊥BD,如图3所示,以E为坐标原点,分别以EF、ED、EA所在直线为x、y、z轴,建立空间直角坐标系E-xyz.不妨设AB＝BD＝DC＝AD＝2,则 BE＝ED＝1.

图3

当然本题也可利用几何法来证明:由题目条件可知BD⊥AE,BD⊥EF,所以BD⊥面AEF,所以BD⊥AF.

2 求解空间角

空间角包括:线线角、线面角、二面角.其中:线线角可利用2直线方向向量所成角来求解;线面角可利用直线的方向向量和平面的法向量所成角与所求线面角的互余关系求解;二面角可利用2平面的法向量所成的角与二面角相等或互补的关系求解.

将二面角转化为2个平面的法向量所成的角进行求解时,要注意二面角的平面角是锐角还是钝角,从而决定所求得的余弦值是取正还是取负.当不好判断时可以利用以下结论:设A、B分别是平面α、β上的2点,且都不在平面α与β的交线上,n、m分别是α、β的法向量,θ为平面α、β平面角.当同号时,二面角的平面角大小为arccos当异号时,二面角的平面角大小为π－arccos

图4

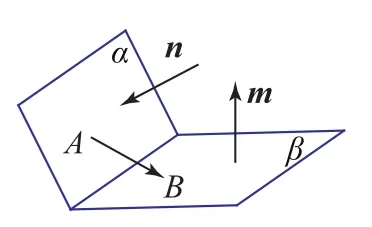
图5

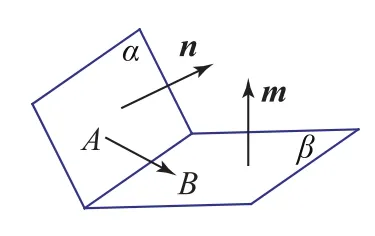
图6

图7

3 判断空间平行关系

空间平行关系包括:线线平行、线面平行、面面平行.其中:线线平行可利用2直线的方向向量成比例的关系来判断;线面平行可利用平面的方向向量与平面的法向量垂直来判断;面面平行可利用2平面的法向量平行来判断.

对于是否存在型问题,我们可先假设其存在,再利用所学原理判断其存在的条件与已知是否矛盾,进而实现问题的解答.

利用空间向量解决一些立体几何问题,可以简化原本利用其他数学工具解题的步骤和过程,使学生多掌握一种行之有效的数学工具.但是要注意,首先坐标要正确,运算要过关.

(作者单位:江苏省南京市高淳区湖滨高级中学)