把握本质,触类旁通——仅以2016年高考全国卷第23题的解法

◇ 贵州 罗 轩北京 童嘉森(特级教师)

把握本质,触类旁通
——仅以2016年高考全国卷第23题的解法

◇ 贵州 罗 轩1北京 童嘉森2(特级教师)

虽然新课程实施已经多年,但靠题海战术学习高中数学的情况还是屡见不鲜.事实上,从近些年的高考试题来看,许多考题的解决是有规律可循的,关键在于我们能否揭示其内在规律,并按照一定的解题程序,同时再辅以正确的类比、猜想、发散、推理和运算等.本文从不同角度和方法试图通过探析2016年高考全国卷第23题选修4-4:坐标系与参数方程,从而揭示出该类问题的相应解法和内在规律.

(1)说明C1是哪种曲线,并将C1的方程化为极坐标方程;

(2)直线C3的极坐标方程为θ＝α0,其中α0满足tanα0＝2,若曲线C1与C2的公共点都在C3上,求a.

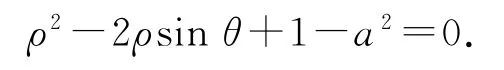
方法1是在极坐标下,利用2曲线C1、C2的公共点在直线C3上且与C3具有相同极角的特点,借助直线C3已知的极角,从而有效解决了此问题,体现了极径和极角的几何意义的重要性.

方法2 将曲线C2:ρ＝4cosθ化为直角坐标方程,即为(x－2)2＋y2＝4,可知曲线C2为以C2(2,0)为圆心,以2为半径的圆,则圆C2一定过原点.因为直线C3的极坐标方程为θ＝α0且tanα0＝2,则直线C3的直角坐标方程为y＝2x,该直线过原点.

又由题意知直线C3与圆C2相交,除了原点O外,还有另一个交点,设此交点为A.由于圆C1与圆C2的公共点都在直线C3上,则直线C3是2圆的公交线,2圆相减所得的方程就是直线C3方程,即为(x2＋y2－2y＋1－a2)－(x2＋y2－4x)＝0,化简得4x－2y＋1－a2＝0.又直线C3方程为y＝2x,所以1－a2＝0,解得a＝±1.经验证a＝1符合题意,故a＝1.

方法2是在直角坐标系下,利用2圆相交的性质特征,把2圆的方程相减,就得到公共直线的方程.该题的公共直线方程已知,反过来求圆C1中的a,不失为一种重要的解题方法.

方法3是利用圆和直线的参数方程解决问题的,寻求它们参数的几何意义以及各参数之间的联系作为解题的突破口,从中理解参数所代表的几何意义和功能是解题的关键所在.

例2 (2016年全国卷Ⅱ)在直角坐标系xOy中,圆C的方程为(x＋6)2＋y2＝25.

(1)以坐标原点为极点、x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;

(1)将ρ2＝x2＋y2,x＝ρcosθ代入圆C的方程(x＋6)2＋y2＝25中,得极坐标方程ρ2＋12ρcosθ＋11＝0.

(2)方法1 在(1)中建立的极坐标系中,直线l的极坐标方程为θ＝α(ρ∈R).设A、B2点所对应的极径分别为ρ1、ρ2,将l的极坐标方程θ＝α(ρ∈R)代入C的极坐标方程ρ2＋12ρcosθ＋11＝0中得ρ2＋12ρcosα＋11＝0.于是有ρ1＋ρ2＝－12cosα,ρ1ρ2＝11.由极径的几何意义|AB|＝|ρ2－ρ1|＝所以直线l的斜率为

方法1充分运用极径和极角的几何意义,把求弦长恰好转化为2极径之差,体现了极坐标的内在威力.

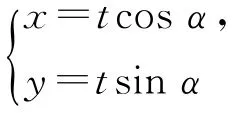
方法2充分运用直线参数方程中参数t的几何意义,把求弦长恰好转化为A、B2点分别对应的参数t1、t2之差的绝对值,即为|AB|＝|t2－t1|,体现了直线参数方程中参数t所代表的形与数的内在转化规律,所以理解t的几何意义是解决问题的关键,实际上此解法的参数t与方法1中的极径ρ本质上是一致的.

方法3是在直角坐标系下先考查了直线与圆的位置关系,充分运用圆的几何性质中的垂径定理,直接建立弦长、半径和圆心到直线的距离之间的关系,从而得到了直线的斜率,体现了垂径定理解决问题的优越性.

例3 (2016年全国卷Ⅲ)在直角坐标系xOy中,曲线C1的参数方程为(θ为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为

(1)写出C1的普通方程和C2的直角坐标方程;

(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.

本题可按上述方法求解,过程略.

以上3例虽然形式不一样,但实质是相通的.既可以从极坐标系中利用极径和极角的几何意义去解决,也可以用参数方程中参数的几何意义去解决,还可以在直角坐标下,利用普通方程中所表示的几何特征去解决,甚至可以把它转化为函数来解决.考生在通性通法中可择优选取,以达到做一题通一类的目的,真正做到突破本质,触类旁通.

(作者单位:1.贵州贵阳实验三中2.北京市第八十中学)