p-达朗贝尔判别法及其应用
张玉林, 孟 程, 赵茂先, 董晓敏, 葛晓晶
(1.山东科技大学数学与系统科学学院,山东青岛266590; 2.山东科技大学信息科学与工程学院,山东青岛266590)
p-达朗贝尔判别法及其应用
张玉林1, 孟 程2, 赵茂先1, 董晓敏1, 葛晓晶1
(1.山东科技大学数学与系统科学学院,山东青岛266590; 2.山东科技大学信息科学与工程学院,山东青岛266590)
对正项级数的达朗贝尔判别法作了推广,提出并证明了p-达朗贝尔判别法,扩大了其使用范围.进一步利用数列和子列的收敛关系,证明了其与柯西判别法之间的关系.最后通过例子对p-达朗贝尔判别法进行了验证.
正项级数; 达朗贝尔判别法; 柯西判别法; 收敛性
1 引 言
在级数理论中,研究正项级数,特别是判别其收敛性或发散性有很多方法,如达朗贝尔判别法,柯西判别法,拉贝判别法与对数判别法[1],或将达朗贝尔判别法及柯西判别法结合起来得到新的判别法,如D-C判别法[2]和Z判别法[3].这些方法从不同角度探讨了如何判断正项级数的敛散性.本文针对达朗贝尔判别法的不足,提出了一种改进的p-达朗贝尔判别法,并证明了p-达朗贝尔判别法与柯西判别法的关系,最后给出了相关的例子进行了验证.


在判定正项级数的敛散性时,这两种方法经常要用到.但是,柯西判别法的适用范围要比达朗贝尔判别法的适用范围更广[4].即凡能用达朗贝尔判别法判定出敛散性的正项级数,用柯西判别法也一定能判定.反之,用柯西判别法能判定出敛散性的正项级数,用达朗贝尔判别法却未必能判定.
解 用柯西判别法判定,因为
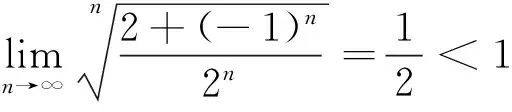
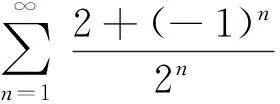
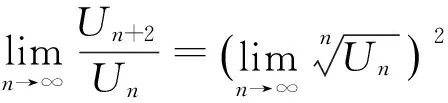
这个例子启发我们,能否对达朗贝尔判别法进行推广,用来判别类似于上述例1形式的正项级数的敛散性.
2 推广的达朗贝尔判别法
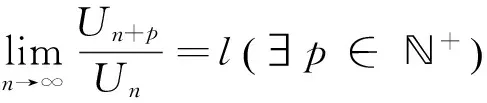

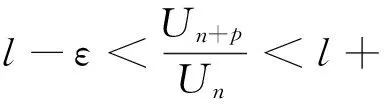
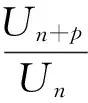
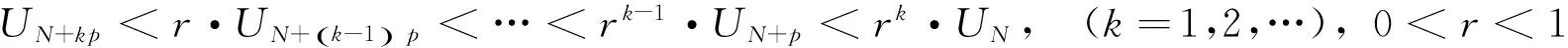
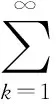

3 p-达朗贝尔判法与柯西判别法的关系
当p=1时,达朗贝尔判别法与柯西判别法的关系见参考文献[4],下面对p>1时,对p-达朗贝尔判别法与柯西判别法的关系予以证明.在证明的过程中,要用到数列和子列的收敛关系,故给出引理,利用子列的收敛性判断数列的收敛性.利用该引理,证明了p-达朗贝尔判别法与柯西判别法的关系.
定义1[5]对于非空集合S, 设S1,S2,…,Sn是其一系列非空子集,满足

则称S1,S2,…,Sn是集合S的一个n类分划.
定义2[5]设无限集合N1,N2,…,Np是自然数集合+的一个p类分划,且这些集合N1,N2,…,Np中的元素均为从小到大排列,则对于数列,以N1,N2,…,Np为下标集,构成了数列的p个子列,分别记为},称为分数列的p类子数列.






同理,可得
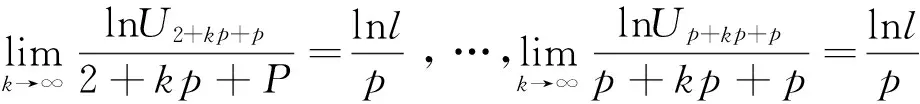


UN+2p+1 同理,得 解 令p=2,则 由定理4得 这也验证了定理4的正确性. 解 令p=2,则 则由定理3,无法判断此正项级数的敛散性.事实上,用比较判别法的极限形式,可以得出该级数是发散的.因为 [1] 李亚兰. 正项级数拉阿贝判别法等价形式及其应用[J]. 大学数学, 2011, 27(4):192-195. [2] 张永明. 正项级数的D—C判别法[J].大学数学,2002,18(2):95-96. [3] 张国铭.“正项级数收敛性的一种新的判别法”的注记[J].大学数学, 2010,26(4):200-201. [4] 曹学锋,孙幸荣.D′Alembert判别法与Cauchy判别法的强弱比较[J].长春理工大学学报(高教版).2008,3(1):173-174. [5] 钱云.“数列的子列及其分类”[J].高等数学研究,1999,2(3):7-8. Thep-D’Alembert Method and its Application ZHANGYu-lin1,MENGCheng2,ZHAOMao-xian1,DONGXiao-min1,GEXiao-jing1 (1. College of Mathematics and System Science, Shandong University of Science and Technology, Qingdao Shandong 266590, China;2. College of Information Science and Engineering, University of Science and Technology Qingdao Shandong 266590, China) D′Alembert discriminance is promoted to thep-D′Alembert discrimination for positive series, and then the correspondingp-D′Alembert discrimination is proved. Further convergence relation of sequence and its sub-sequence is used to discuss the relationship between the discrimination and Cauchy discrimination. Finally, some examples of this method are verified. positive series; D’Alembert Discrimination; Cauchy discrimination; convergence 2015-10-19; [修改日期]2016-06-02 山东科技大学人才引进科研启动基金(2014RCJJ033);国家自然科学基金(61572128) 张玉林(1979-),男,博士,讲师,从事机器学习方面的研究.Email:zhangyulin@sdust.edu.cn O174 C 1672-1454(2016)05-0071-05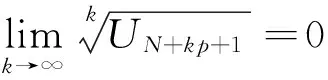


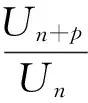
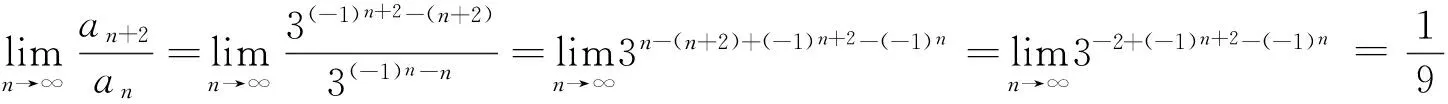




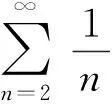
4 结 论