一个含特殊常数因子的非齐次核Hilbert型不等式

有名辉

(浙江机电职业技术学院数学教研室，浙江杭州 310053)

一个含特殊常数因子的非齐次核Hilbert型不等式

有名辉

(浙江机电职业技术学院数学教研室，浙江杭州 310053)

通过引进参数，利用权函数的方法，建立了一个最佳常数因子与余割函数有关的Hilbert型积分不等式及其等价形式．作为应用，赋予参数不同的值，文中还给出了一些新的特殊结果．

Hilbert型不等式；非齐次核；余割函数；权函数；Gamma函数

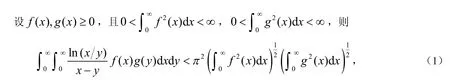
其中π2是满足（1）式的最佳常数因子[1]，通常称不等式（1）为Hilbert型不等式．由于Hilbert型不等式在分析学及其应用领域中有重要的作用[2]，所以一直以来是很多数学工作者热衷研究的对象．近年来，通过引进参数，研究者们[3-13]给出了（1）式及其对应的级数形式的一些推广和改进，取得了一系列有价值的成果．最近，陈小雨等[14]给出了一个类似于（1）式的非齐次核的Hilbert型不等式：

1 定义及引理

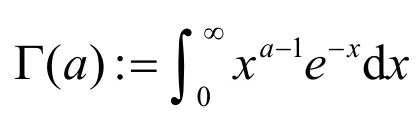
证明：由φ(x)=cscx 的部分分式展开形式[15]

（3）式两边关于x求2n阶导数，得

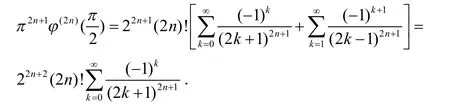
引理1得证．

引理2 设λ＞0，n为非负整数，φ(x)=cscx ，则

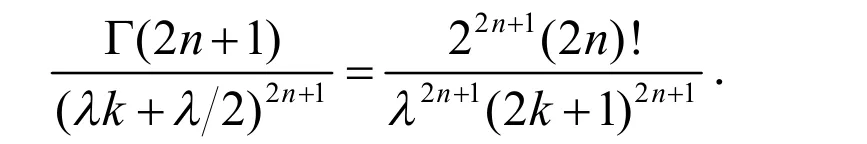
因此

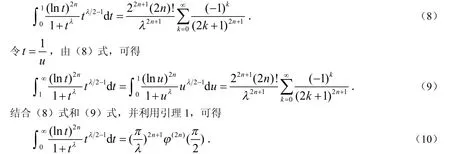
把（10）式代入到（7）式，便得（5）式．类似地，可得（6）式．

引理2证毕．

令ε→0+，由引理2，可得

由（11）式和（12）式，即得引理3．

2 定理及证明

证明：由Hölder不等式，可得盾．故（14）式不取等号．

根据引理2，（14）式可改写为

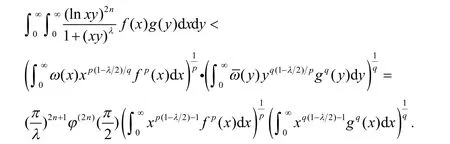
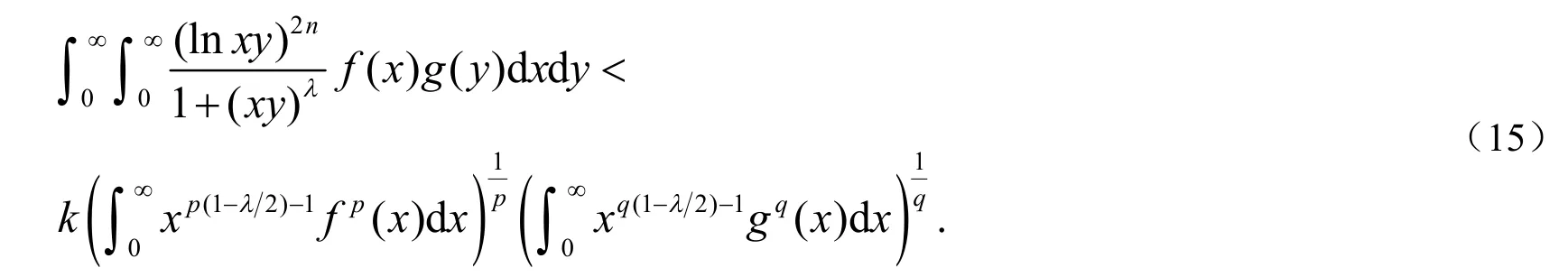
用引理3中定义的fε和gε分别取代（15）式中的f和g，则

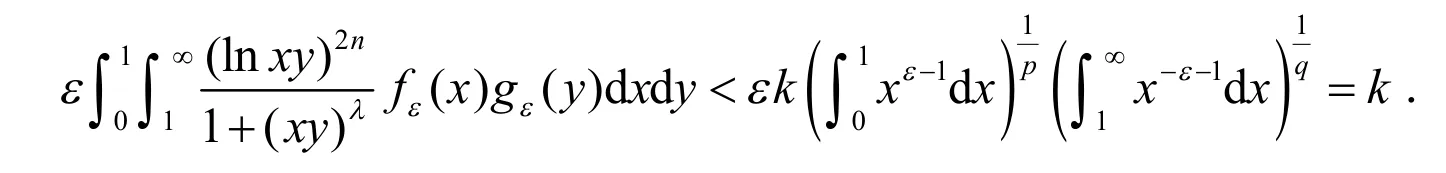
定理1证毕．

结合定理2的条件和（18）式可知应用定理1的条件是充分的．因此（17）式和（18）式都取严格不等号．

故（16）式成立．

以上从（13）式证得了（16）式．要说明（13）式和（16）式等价，以下只需从（16）式证得（13）式．事实上，由Hölder不等式，可知

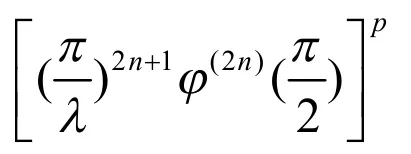
定理2证毕．

赋予定理1中的参数不同的值，可以得到一些特殊的结果．如：在定理1中，令n=0，则有以下推论．

[1] Hardy G H, Littlewood J E, Polya G. Inequalities [M]. London: Cambridge Univ Press, 1952: 255.

[2] Mintrinovic D S, Pecaric J E, Fink M. Inequalities involving functions and their integrals and derivatives [M]. Boston: Kluwer Academic, 1991: 79-135.

[3] 杨必成. 关于一个Hilbert类积分不等式的推广及应用[J]. 应用数学, 2003, 16(2): 82-86.

[4] 杨必成. 一个推广的Hilbert型积分不等式及其应用[J]. 数学杂志, 2007, 27(3): 285-290.

[5] 付向红, 和炳. 具有两个参数的Hilbert型积分不等式[J]. 吉林大学学报(理学版), 2010, 48(4): 595-599.

[6] Kuang J, Debnath L. On new generalizations of Hilbert’s inequality and their applications [J]. J Math Anal Appl, 2000, 245(1): 248-265.

[7] 杨必成. 关于一个推广的具有最佳常数因子的Hilbert类不等式及其应用[J]. 数学研究与评论, 2005, 25(2): 341-346.

[8] 杨必成. 一个推广的具有最佳常数因子的Hilbert型不等式[J]. 吉林大学学报(理学版), 2006, 44(3): 333-337.

[9] 杨必成. 一个较为精密的Hardy-hilbert型不等式及其应用[J]. 数学学报(中文版), 2006, 49(2): 363-368.

[10] Jin J. A new generalization of Hardy-hilbert type inequality with multi-parameters [J]. J Math Res Exposition, 2009, 29(6): 1131-1136.

[11] 孙保炬. 一个推广的Hardy-hilbert型不等式[J]. 科技通报, 2012, 28(5): 18-23.

[12] Jin J. On Hilbert’s type inequalities [J]. J Math Anal Appl, 2008, 340(2): 932-942.

[13] 杨必成. 关于一个基本的Hilbert型积分不等式及推广[J]. 大学数学, 2008, 24(1): 87-92.

[14] 陈小雨, 高明哲, 黄政. 具有Catalan常数的Hilbert型积分不等式[J]. 南京大学学报(数学半年刊), 2013, 30(1): 95-103.

[15] 菲赫金哥尔茨. 微积分学教程: 第二卷[M]. 徐献瑜, 冷生明, 梁文骐, 译. 北京: 高等教育出版社, 2006: 625-639.

[16] 匡继昌. 常用不等式[M]. 济南: 山东科学技术出版社, 2003: 5.

[17] 杨必成. 算子范数与Hilbert型不等式[M]. 北京: 科学出版社, 2009: 307.

The Study of a Hilbert-Type Inequality Involving Non-homogeneous Kernel with Special Constant Factor

YOU Minghui
(Mathematics Teaching and Research Section，Zhejiang Institute of Mechanical and Electrical Engineering, Hangzhou, China 310053)

By means of the method of the in-put of parameters with the application of weight function，this paper establishes a Hilbert-type integral inequality and its equivalent form combined the optimum constant factor with the cosecant function. As applications, giving the parameters different values, some new and special results are considered in such a research．

Hilbert-type Inequality; Non-homogeneous Kernel; Cosecant Function; Weight Function； Gamma function

O178

A

1674-3563(2016)04-0017-08

10.3875/j.issn.1674-3563.2016.04.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2015-05-18

有名辉(1982- )，男，浙江安吉人，讲师，硕士，研究方向：解析不等式