求解奇异鞍点问题的参数化预条件HSS方法

吕月燕，张乃敏

(温州大学数学与信息科学学院，浙江温州 325035)

求解奇异鞍点问题的参数化预条件HSS方法

吕月燕，张乃敏†

(温州大学数学与信息科学学院，浙江温州 325035)

利用参数化预条件HSS迭代方法对奇异的大型稀疏线性系统进行了求解，分析了该方法的半收敛性和参数的最优选取问题，并且与其它方法进行了比较．数值实验结果表明：参数化预条件HSS迭代方法在求解奇异鞍点问题时比其它方法更有效．

奇异鞍点问题；预条件；迭代方法；半收敛性；线性系统

考虑以下线性系统的迭代解：

其中B∊Cp×p是Hermitian正定矩阵，E∊Cp×q是列秩亏的，p≥q，E*为E的共轭转置，f∊Cp，g∊Cq．（1）形式的线性系统统称为鞍点问题，在现代科学的诸多领域都有广泛应用[1-2]．

当大型稀疏线性系统（1）的系数矩阵为非奇异时，那么矩阵E是列满秩的，系统（1）被称为非奇异鞍点问题．解决此类问题的迭代方法已有不少，例如，白中治等提出了一系列的预条件Hermitian和Non-Hermitian分裂方法（PHSS）[3]及加速Hermitian和Non-Hermitian分裂方法（AHSS）[4]．当线性系统（1）的系数矩阵为奇异时，即E为列秩亏矩阵，被称为奇异鞍点问题．解决此类问题的方法也有不少，例如，郑兵等提出了参数Uzawa方法[5]，马海凤等研究了块对角PPIU方法[6]等．本文将利用参数化预条件HSS迭代方法（PPHSS）对奇异鞍点问题进行求解，数值实验结果表明，参数化预条件HSS迭代方法在求解奇异鞍点问题时比其它方法更有效．

1 参数预条件HSS方法

对线性方程组（1）的系数矩阵A进行如下HSS分裂[7]：

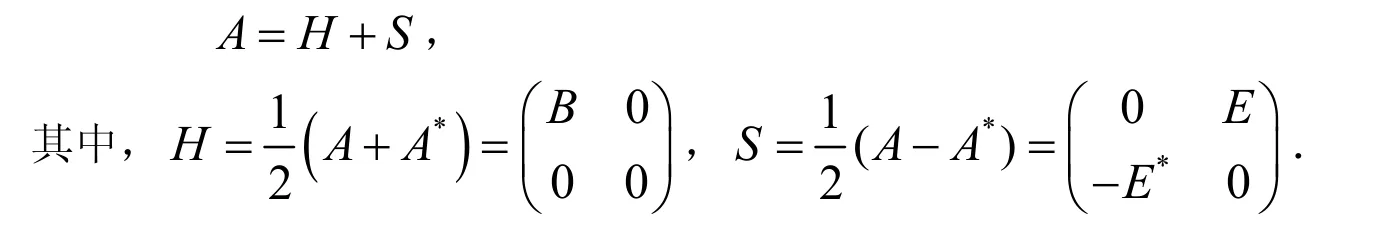
PPHSS迭代方法：记n=p+q，令x(0)∊Cn为初始向量，采用如下的迭代形式：

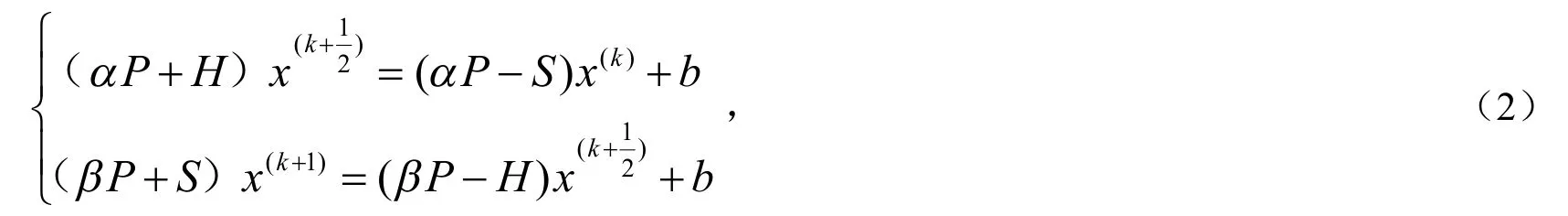
其中α和β是给定的正实数，矩阵P取如下形式：

此处C是一个Hermitian正定矩阵．显然，PPHSS方法的迭代格式（2）可以等价于

其中，

这里的T(α,β)是PPHSS方法的迭代矩阵，Ip和Iq是阶数分别为p和q的单位矩阵．实际上，（4）可由下面的分裂得到：

经过简单的计算，可得：

显然，矩阵M(α,β)可以作为一个预条件子用来求解线性方程组（1），称为PPHSS预条件子．为了进一步分析PPHSS迭代的半收敛性，用另一种等价的形式来替代该迭代．记

2 PPHSS方法的半收敛性分析

对于定常迭代（4），我们知道如果系数矩阵A是非奇异的，那么定常迭代收敛当且仅当迭代矩阵谱半径小于1．若系数矩阵A是奇异的，迭代矩阵有特征值1，所以它的谱半径不会比1小，对于这种情况的迭代矩阵T，我们介绍它的拟谱半径ν(T)：ν(T)=max｛|λ|:λ∊σ(T),λ≠1｝，其中σ(T)表示迭代矩阵T特征值的集合．对于任何矩阵K∊Cn×n，如果i是使得rank(Ki)=rank(Ki+1)成立的最小非负整数，那么i称做矩阵K的指标，记为i=index(K)．实际上，index(K)是矩阵K的零特征值对应的最大Jordan块的阶数．

引理1[8]迭代方法（4）半收敛当且仅当index(I-T(α,β))=1且ν(T(α,β))＜1．

引理2[9]index(I -T(α,β))=1，当且仅当，对任意的0≠Y∊R(A)，Y ∉N(AM-1)，其中，R(·)和N(·)分别为相应矩阵的值域和零空间．

定理1 对于（4）中的迭代矩阵T(α,β)，有index(I-T(α,β))=1成立．

证明：令

引理4 迭代矩阵T(α,β)的特征值λ按以下情形分布：

引理6[9]实二次方程x2-bx+c=0的根均小于1，当且仅当|c|＜1和|b|＜1+c．

定理2 如果迭代参数α和β满足：

那么，PPHSS方法迭代矩阵的拟谱半径满足ν(T(α,β))＜1．

3 数值实验

本节将给出一个例子，通过与其它有效的迭代方法比较迭代步数（IT）、CPU耗时（CPU）、迭代残差（RES）来判断PPHSS方法及其作为预条件子（PPHSS-GMRES）的有效性．在下面的实验中，初始向量x(0)取为令向量，一旦迭代满足条件

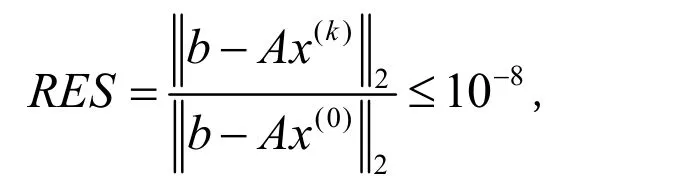
或者迭代次数超过1 000则迭代终止．所有实验将利用Matlab[version 7.0.0.19920(R14)]解决，在Intel(R)Celeron(R)CPU 1000M @1.80GHz，内存2GB的个人电脑上运行．

例1[5]对于奇异鞍点问题（1）中的块矩阵有如下形式：

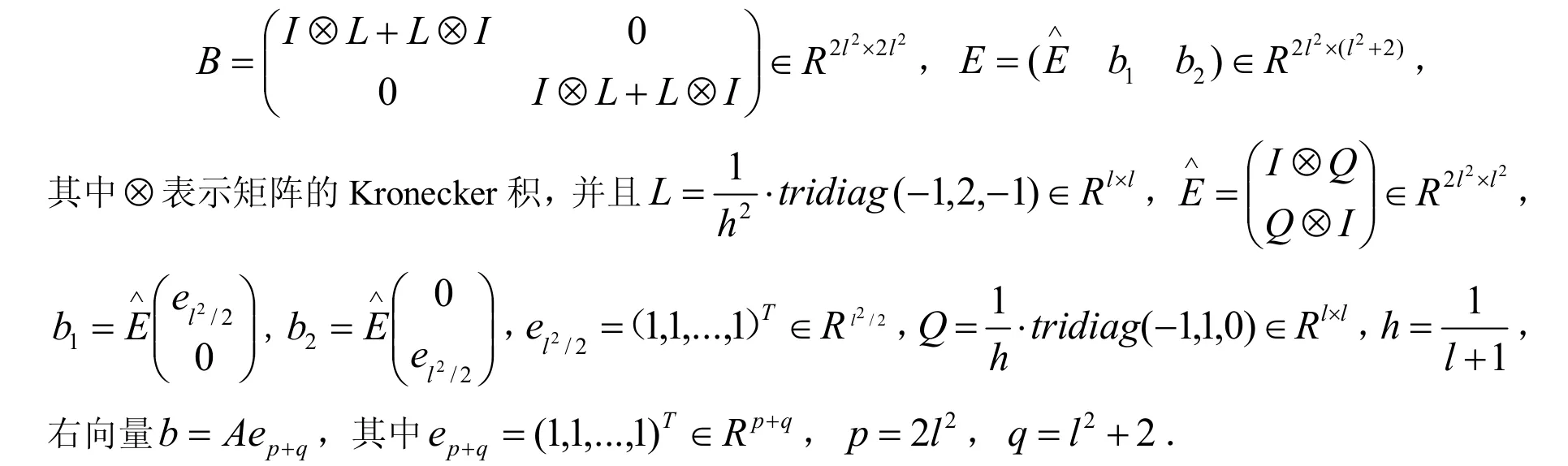
关于矩阵P，对其中的C取两种情况．情况I：C=I；情况II：其中B*是矩阵B的块对角阵．两种情况下，各迭代方法的最优参数和拟谱半径见表1，IT，CPU，RES分别见表2和表3．从表1可以发现，l越大，相同方法的拟谱半径也越大．从表2和表3可以发现，在给定合适的参数后，PPHSS方法不管是在迭代步数还是迭代时间上都比其它方法少，这说明PPHSS方法是比较有效的．从表2和表3还可以看出，PPHSS预条件子和SPPHSS预条件子都能够很有效地改善GMRES算法的收敛速度．注意，

表1 实验例1中各方法的最优参数和拟谱半径

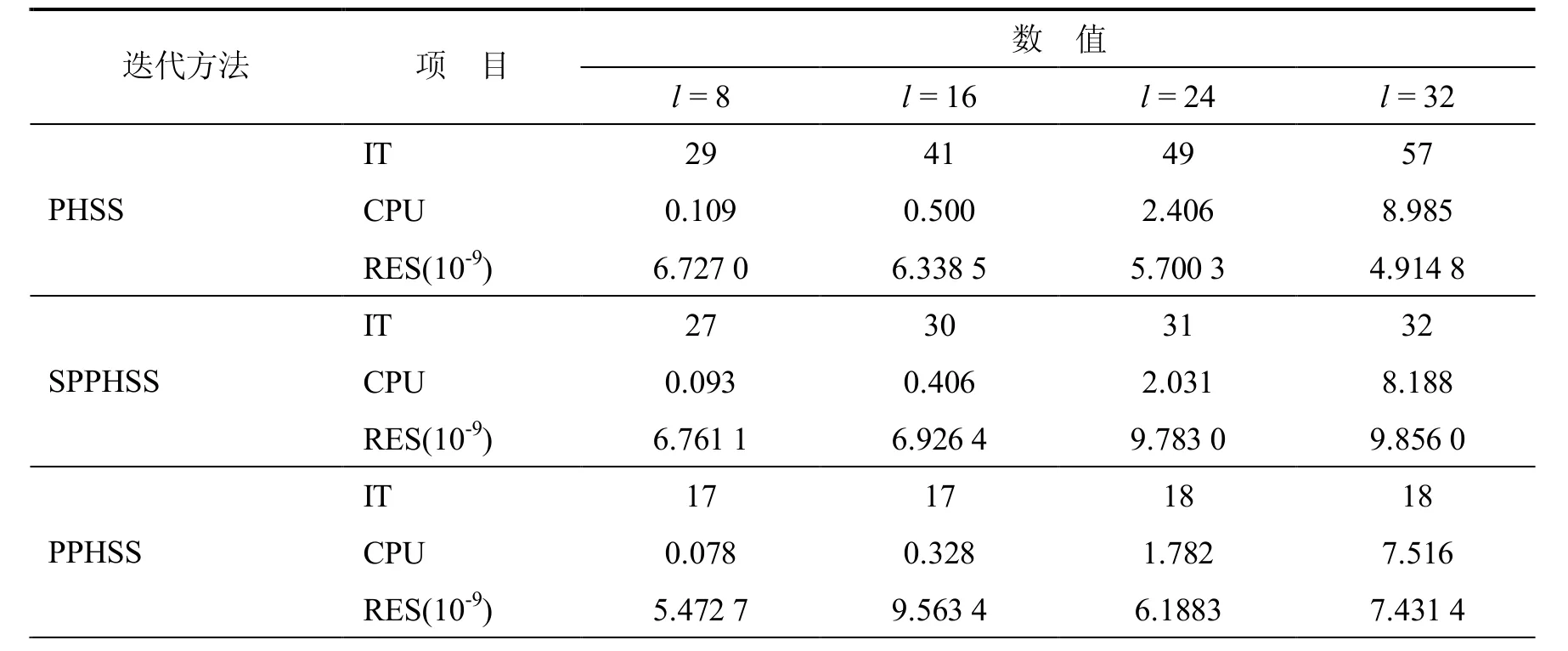
表2 情况I时各迭代方法的IT, CPU, RES

迭代方法 项 目 l=8 l=16 l=24 l=32数 值IT 883 2560 5450 10376 GMRES CPU 0.524 3.179 12.572 16.264 RES(10-9)9.824 3 9.992 5 9.990 3 9.995 0 IT 18 27 31 35 PHSS-GMRES CPU 0.052 0.344 1.350 3.656 RES(10-9)5.990 0 5.371 9 3.321 7 8.675 5 IT 9 12 13 14 SPPHSS-GMRES CPU 0.033 0.295 1.310 3.497 RES(10-9)3.702 2 1.574 3 4.132 4 7.064 2 IT 10 12 14 15 PPHSS-GMRES CPU 0.035 0.296 1.333 3.501 RES(10-9)5.916 1 9.087 0 5.526 2 9.202 2

表3 情况II时各迭代方法的IT, CPU, RES

本文主要对参数化预条件HSS方法求解奇异鞍点问题的半收敛性进行了研究，并分析了参数的最优选取方法．在上述内容的研究过程中也遇到了一些问题，有待于日后进一步研究探索．

[1] Elman H C, Ramage A, Silvester D J. A Matlab toolbox for modelling incompressible flow [J]. ACM Trans Math Softw, 2007, 33: 1-18.

[2] Wright S. Stability of augmented system factorization in interior-piont methods [J]. SIAM J Matrix Anal Appl, 1997, 18: 191-222.

[3] Bai Z Z, Golub G H, Pan J Y. Preconditioned Hermitian and skew-Hermitian Splitting methods for non-Hermitian positive semidefinite linear systems [J]. Numer Math, 2004, 98: 1-32.

[4] Bai Z Z, Golub G H. Accelerated Hermitian and skew-Hermitian splitting iteration methods for saddle-point problems [J]. SIAM J Numer Anal, 2007, 27: 1-23.

[5] Zheng B, Bai Z Z, Yang X. On semi-convergence of parameterized Uzawa methods for singular saddle point problems [J]. Linear Algebra Appl, 2009, 431: 808-817.

[6] Ma H F, Zhang N M. A note on block-diagonally preconditioned PIU methods for singular saddle point problems [J]. Int J Comput Math, 2011, 88: 3448-3457.

[7] Bai Z Z, Golub G H, Ng M K. On inexact Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems [J]. Linear Algebra Appl, 2008, 428: 413-440.

[8] Abraham B, Plemmons R J. Nonnegative Matrices in the Mathematical Science [M]. New York: SIAM, 1994: 43-52.

[9] Zhang N M, Wei Y M. On the convergence of general stationary iterative methods for Range-Hermitian singular linear systems [J]. Numer Linear Algebra Appl, 2010, 17: 139-154.

[10] Li X, Yang A L, Wu Y J. Parameterized preconditioned Hermitian and skew-Hermitian splitting iteration method for saddle-point problems [J]. Int J Comput Math, 2014, 91: 1224-1238.

[11] Golub G H, Van Loan C F. Matrix Computions [M]. 3rd ed. Baltimore: The Johns Hopkins University Press, 1996: 23-27.

The Study of the Parameterized Preconditioned HSS Method to Solve Singular Saddle Point Problems

LV Yueyan, ZHANG Naimin
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)

In this paper, the HSS iterative method is used to solve the large-scale singular sparse linear system by means of the parameterized precondition. The method of the semi-convergence and the optimal parameter selection problem is analyzed and meanwhile compared with other methods. Numerical experimental results show that the parameterized preconditioned HSS iterative method in the field of the singular saddle point problemsolution is more effective than other methods.

Singular Saddle Point Problem; Precondition; Iterative Method; Semi-convergence; Linear System

O241

A

1674-3563(2016)04-0001-08

10.3875/j.issn.1674-3563.2016.04.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2015-09-29

国家自然科学基金(61572018)；浙江省自然科学基金(LY15A010016)

吕月燕(1991- )，女，江西九江人，硕士研究生，研究方向：计算数学．†通讯作者，nmzhang@wzu.edu.cn