关于Hölder不等式和Minkowski不等式的一个注记

徐彦辉

(温州大学数学与信息科学学院，浙江温州 325035)

关于Hölder不等式和Minkowski不等式的一个注记

徐彦辉

(温州大学数学与信息科学学院，浙江温州 325035)

本文给出了Hölder不等式和Minkowski不等式的一个推广．

Hölder不等式；Minkowski不等式；推广

Hardy等再三强调Hölder不等式和Minkowski不等式“极为重要”和“到处都要用到”，一百多年来，对这两个不等式的种种改进和推广工作一直没有中断[1]11．本文给出了Hölder不等式和Minkowski不等式的一个推广．

1 Hölder不等式的推广

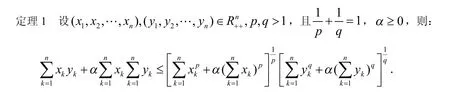
为证明定理1，先给出一个引理．

引理1（Young不等式）[1]7：设a,b≥0，0＜λ＜1，则aλb1-λ≤λa+(1-λ)b ，当且仅当a=b时等号成立．

定理1的证明：要证原不等式成立，即只要证：

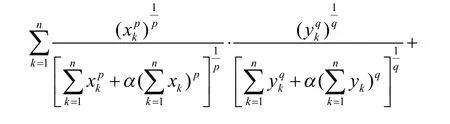
2 Minkowski不等式的推广

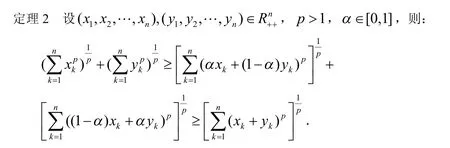
为证明定理2，先给出引理2．

引理2（Minkowski不等式）[1]8设则

定理2的证明：由Minkowski不等式得：

[1] 匡继昌. 常用不等式[M]. 3版. 济南: 山东科学技术出版社, 2004.

A Note on Hölder Inequality and Minkowski Inequality

XU Yanhui
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)

The refinement of Hölder Inequality and Minkowski Inequality is given in this paper.

Hölder Inequality; Minkowski Inequality; Generalization

O178

A

1674-3563(2016)04-0014-03

10.3875/j.issn.1674-3563.2016.04.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2015-10-20

教育部人文社科2012年青年基金项目(12YJC880131)

徐彦辉(1975- )，男，江西丰城人，副教授，博士，研究方向：数学教育和解析不等式