三星干扰源定位中ETDE时差算法的研究∗

牟庆丰，顾 平，张荣芬

(贵州大学大数据与信息工程学院，贵州贵阳550025)

三星干扰源定位中ETDE时差算法的研究∗

牟庆丰，顾 平，张荣芬∗

(贵州大学大数据与信息工程学院，贵州贵阳550025)

在三星系统干扰源定位的时差(TDOA)估计中，ETDE约束算法不仅在不相关噪声情况下可以很好的估计时差值，在相关噪声情况也可以很好的估计时差值，但其存在着明显的缺点即只有在滤波器阶数趋于无穷或很大的情况下才能估计出时差值，而且在两路信号信噪比差变大的情况下，该算法对时差的估计效果也会下降。针对以上缺点本文提出改进的ETDE算法——ETDGE算法，该算法不仅可以在较小的滤波器阶数下对时差进行准确估计，在两路信噪比大幅度变化的情况也能达到准确估计时差的目的。

三星干扰源定位;TDOA;ETDE算法;ETDGE算法

随着卫星通信技术的蓬勃发展，卫星已经在商用和民用中体现出巨大的价值。但由于现代社会通讯设备的大量普及，导致电磁环境的恶化，大量干扰源影响着卫星定位的精确性以及卫星通信的质量。所以对干扰源的定位成为了不可或缺的技术，对干扰源的定位关系着卫星相关技术的正常使用，同时对维权和卫星通信安全也起着重要的作用。

而对卫星干扰源定位的诸多技术中，三星定位凭借其简单的计算方法，不需要外加过多的设备，以及成熟的技术等诸多优点得到了广泛的应用。三星定位的技术关键是要得到两个精确的时差(TDOA:time difference of arrival)，这样才能对干扰源进行准确的定位。

三星干扰源时差定位技术是利用一些估计算法测量出两路TDOA参数值，然后通过两次定位计算得出两条时差线，它们在地球表面上的交点就是干扰源的位置。所以，选取能够快速、精确的时延估计算法尤为重要。约束类算法 ETDE(explicit time delay estimation)无论是在不相关噪声条件下还是相关噪声条件下都可以较为准确的估计时延，其改进算法也是约束类算法，在其基础上保留了ETDE原算法的优点，也可克服其需要高阶滤波和信噪比变化带来估计不准的缺点，增强了原算法的使用条件和准确性。

本文在研究ETDE算法的基础上，对更适合于TDOA估计的ETDE改进算法(具有较小滤波器阶数及能够增加两路信噪比变化范围)的ETDGE算法进行了探讨与分析，并通过matlab仿真平台对两种算法进行比对，意在为三星干扰源定位时能准确得到TDOA延时参数提供仿真依据。

1 信号模型

传输延时信号的模型由两路信号组成，如式(1)与(2)所示:

式中:s(t)为干扰源信号，x(t)与y(t)分别是受干扰卫星与其相邻卫星接收的地面干扰源信号，A为振幅系数，m1、m2为独立分布的加性噪声，D是干扰源向两星传输的时间延迟差值。

将式(1)与(2)离散化可写成:

2 算法说明

2.1 ETDE算法

ETDE算法属于最小均方误差方法的一种，与传统的LMSTDE算法相比，它在相关噪声条件下有更好的估计时差的能力，其算法原理与LMSTDE算法接近，其原理是利用一个形式为:

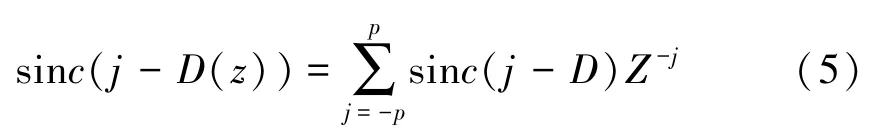
的非因果滤波器来拟合x(t)和y(t)两路信号的延时值。每个滤波器的系数由迭代得来:

式中:u是一个正的系数，用于控制迭代的速度和稳定性，而输出误差可以表示为:

通过以上公式不难分析出每个滤波器的系数皆与时间延迟D(n)有关。时延的递推公式可以通过对e(n)2求关于D(n)的偏导数得到:

式中，

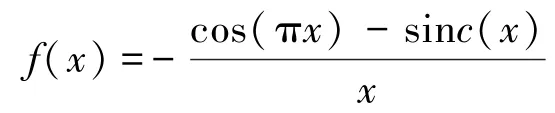
为了计算方便我们设

延迟信号表达式为

将式(9)带入式(6)后，再将式(10)带入式(6)，并取数学期望，则有

式中

式中:ki(0)表示滤波器初值，l的值在-1与1之间，所以当算法收敛后，ETDE算法对时延的估计值为

这证明当ETDE算法收敛后，滤波器的权值将会出现一个峰值，这个峰值的位置就是时延值。

2.2 ETDGE算法

ETDGE是在ETDE算法的基础上改进的一种约束类算法，它保留着原有算法的优点，无论是不相关噪声条件下还是相关噪声条件都能较为准确的估计时延值。同时也改进了原有算法需要高阶滤波器和信噪比变化带来影响的诸多缺点。

ETDGE算法结构与ETDE算法的结构类似，它的滤波器系数为sin c(i-D(n))的形式，同时还增加了一个增益g(n)的迭代。这个增益可以跟踪SNR/(1+SNR)因子，能够帮助ETDGE算法得到准确的时延估计。

ETDGE算法的误差函数为

ETDGE算法的迭代公式为

式中:ug、uD是遗忘因子。

3 实验仿真

3.1 信噪比变化情况下的性能仿真

本文用matlab软件进行仿真，地面干扰信号由rand函数随机产生，码元个数为512，SNR1、SNR2分别为两通道的信噪比，在仿真时我们设SNR1＝5 dB，SNR2＝0，5，10，20，30 dB来观察两种算法的性能。由于这两种算法皆不受相关性的影响，所以以下实验都在相关噪声环境下进行，滤波器的阶数也相同。

(1)当 SNR1＝5 dB，SNR2＝0 dB时，时延TDOA的仿真结果如图1所示。此时，两种算法都能准确的估计出时延，ETDE算法和ETDGE算法的性能很好。

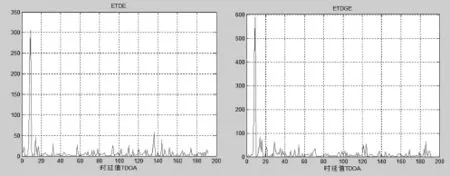
图1 ETDE算法和ETDGE算法的仿真结果

(2)当 SNR1＝5 dB，SNR2＝5 dB时，时延TDOA的仿真结果如图2所示。此时，两种算法系统下，真实时延值附近都出现较小的伪峰，但两种算法都完全没有受到影响。ETDE算法和ETDGE算法的性能很好。

图2 ETDE算法和ETDGE算法的仿真结果

(3)当SNR1＝5 dB，SNR2＝10 dB时，时延TDOA的仿真结果如图3所示。此时，ETDE算法系统下，在真实时延值附近出现3组较明显的伪峰。而在ETDGE算法系统下，在真实时延值附近只出现3组较小的伪峰。ETDE算法性能较好，ETDGE算法的性能很好。

图3 ETDE算法和ETDGE算法的仿真结果

(4)当SNR1＝5 dB，SNR2＝20 dB时，时延TDOA参数的仿真结果如图4所示。此时，ETDE算法系统下，在真实时延值附近出现1组严重的伪峰，已经严重影响对时延的准确判断。而在ETDGE算法系统下，在真实时延值附近只出现几组较小的伪峰。ETDE算法性能不好，ETDGE算法的性能很好。

图4 ETDE算法和ETDGE算法的仿真结果

(5)当SNR1＝5 dB，SNR2＝30 dB时，时延TDOA参数的仿真结果如图5所示。此时，ETDE算法系统下，在180附近出现1组严重的伪峰，已经不能准确判断时延。而在ETDGE算法系统下，在真实时延值附近只出现几组较小的伪峰。ETDE算法已经不能对时延作出估计，ETDGE算法的性能很好。

图5 ETDE算法和ETDGE算法的仿真结果

综合上述5组仿真结果，我们不难发现在滤波器阶数相同的条件下，SNR1＝5 dB的条件下，SNR2＝0 dB，SNR2＝5 dB时两种方法都能很好的估计出时延值。但当SNR2＝10 dB时，ETDE算法的仿真结果出现了多条伪峰，但不影响估计时延，而ETDGE算法性能良好。当SNR2＝20 dB时，传统的ETDE算法出现的伪峰已经严重影响了对时延值的判断，而ETDGE算法依然性能良好。当SNR2＝30 dB时，ETDE算法已经完全不能对时延值做出估计，而ETDGE仍能准确地对其做出估计。可见当两路信号信噪比的差值增大时，改进算法ETDGE性能更加好，优于传统约束算法ETDE。

3.2 滤波器阶数变化情况下的性能仿真

传统的约束算法ETDE需要滤波器阶数很高的条件下才能准确的估计时延值，而改进的算法ETDGE在此方面也做出了改进，新的算法不但减少了迭代次数减少了计算量，同时也节省了资源，为卫星干扰源定位的实际应用提供了简便的条件。

信噪比SNR1＝5 dB，SNR2＝0 dB，将滤波器的阶数从500开始降到100，观察滤波器阶数下降时两种算法的性能，通过仿真来得出结论。

(1)当P＝500时，时延TDOA参数的仿真结果如图6所示。此时，两种算法都能准确的估计出时延，ETDE算法和ETDGE算法的性能很好。

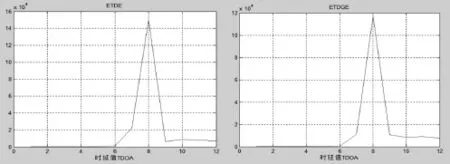
图6 ETDE算法和ETDGE算法的仿真结果

(2)当P＝400时，时延TDOA参数的仿真结果如图7所示。此时，两种算法都能准确的估计出时延，ETDE算法和ETDGE算法的性能均很好。

图7 ETDE算法和ETDGE算法的仿真结果

(3)当P＝300时，时延TDOA参数的仿真结果如图8所示。此时，两种算法系统下，都出现很多较小的伪峰，但都能准确的估计出时延，ETDE算法和ETDGE算法的性能相当。

图8 ETDE算法和ETDGE算法的仿真结果

(4)当P＝200时，时延TDOA参数的仿真结果如图9所示。此时，ETDE算法系统出现多组伪峰。而在ETDGE算法系统下，只出现几组较小的伪峰。说明ETDGE算法的性能较好。

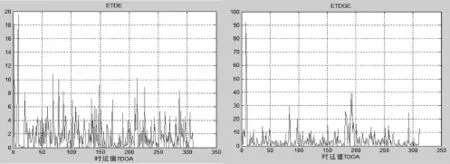
图9 ETDE算法和ETDGE算法的仿真结果

(5)当P＝100时，时延TDOA参数的仿真结果如图10所示。此时，ETDE算法系统下，出现多组伪峰，其中在20附近的伪峰已经干扰了系统对时延的判断。而在ETDGE算法系统下，只出现几组伪峰，其中在20附近的伪峰较为严重，但不影响系统对延时值的准确估计。说明ETDE算法在滤波器的阶数P＝100时已经不能对时延值作出准确的估计，后者仍能准确估计，因此ETDGE算法的性能更好。

图10 ETDE算法和ETDGE算法的仿真结果

通过以上5组实验仿真，我们可以清楚地看到改进的ETDGE算法可以在滤波器很小的条件下准确的估计时延，充分的改进了传统ETDE算法需要高阶滤波器的缺点。当P＝500，400，300时两种算法都能准确地估计出时延参数。当P＝200时，传统ETDE算法出现明显的伪峰，严重影响了对系统时延参数的估计。而当P＝100时，传统算法ETDE已经不能对时延值作出准确的估计，而改进的ETDGE算法仍具备良好的估计性能，弥补了传统ETDE算法的不足。

4 总结

本文主要讲述了传统约束算法ETDE对三星干扰源定位中时延估计的工作原理，并提出了改进的ETDGE约束算法。ETDE算法因为其在相关噪声的条件下能够很好的对时延参数进行估计而广泛使用，但其也有明显的缺点，如在两路信噪比差值增大时其对时延值的估计能力和准确性也在下降，其次传统的ETDE算法也许要很高阶的滤波器才能达到优秀的估计能力，这为实际用制造了诸多问题。本文改进后的ETDGE算法通过改变滤波器的系数和对增益因子g的迭代成功的优化了传统ETDGE的不足。

通过matlab仿真，我们通过改变SNR2来扩大两路信噪比的差值以及降低滤波器阶数P的值两方面对新老两种算法进行性能上的对比，成功验证了改进算法ETDGE对传统约束算法ETDE的优化，实验结果与理论分析吻合。优化的ETDGE算法可以完全取代传统的ETDE算法，并且改进后的ETDGE算法可以在多种条件下对时延参数进行准确的估计，为三星干扰源定位技术提供了行之可效的算法支持。

[1]房利，李选潮，张荣芬.卫星定位中信号时差估计的算法研究[J].计算机仿真，2015，32(4):61-65，78.

[2]廉保旺，赵楠，王永生.三星定位算法的研究[J].弹箭与制导学报，2006，26(1):134-136，139.

[3]刘庆富，卢艳娥，李晓明，等.三星无源定位的精度分析及定位算法[J].航空学报，2008，29(2):456-461.

[4]B.Widrow，S D Stearn.Adaptive Signal Processing[M].Englewood Cliffs:Prentice-HallInc，1993.

[5]Pual L Fentiuhc，Neil JBershad，Frnacis A Reed.Time Delay Estimation Using the LMS Adaptive Filter-Dynamic Behavior[J]. IEEE Transactions on Acoustics，Speech，and Signal Processing，1981，29(3):571-576.

(责任编辑:周晓南)

Research on the ETDE A lgorithm of Three Stars Interference Sources Positioning

MU Qingfeng，GU Ping，ZHANG Rongfen∗

(College of Big Data and Information Engineering，Guizhou University，Guiyang 550025，China)

In three stars system interference sources positioning，the time values of the time difference of arrival (TDOA)can be estimated effectively based on ETDE constraint algorithm under relevant noise or non-relevant noise，but itworks only in the filter when the order toward infinity or a large value and when the signal-to-noise ratio(SNR)difference in two way signals gets bigger.In view of above shortcomings in TDOA，the improved ETDE algorithm-ETDGE algorithm was studied，which can accurately estimate the time difference not only in smaller filter order but also in the case with bigger SNR change of two way signals.

three stars interference source positioning；TDOA；ETDE algorithm；ETDGE algorithm

TN97

A

1000-5269(2016)04-0057-07

10.15958/j.cnki.gdxbzrb.2016.04.12

2015-11-17

贵州大学引进人才科研项目资助(贵大人基合字(2014)30号)；贵州省科技厅贵州大学联合资金项目资助(黔科合LH字[2014]7612)

牟庆丰(1989-)，男，在读硕士，研究方向:软硬件协同、通信技术、模式识别，Email:243328105＠qq.com.

∗通讯作者:张荣芬，Email:zrfen77＠163.com.