一个包含Euler函数方程的正整数解∗

王曦浛，高 丽，鲁伟阳

(延安大学数学与计算机科学学院，陕西延安，716000)

一个包含Euler函数方程的正整数解∗

王曦浛，高 丽∗，鲁伟阳

(延安大学数学与计算机科学学院，陕西延安，716000)

对任意的正整数n，φ(n)是Euler函数，即就是不大于n并与n互素的数的个数。本文主要目的是研究不定方程φ(xyz)＝5(φ(x)+φ(y)+φ(z))的可解性问题，并给出该方程的所有正整数解。

Euler函数;不定方程;正整数解

对于任意的正整数n，φ(n)是Euler函数，即就是不大于n并与n互素的数的个数[1]。有关Euler函数φ(n)的问题，有不少学者研究过且取得不少成果[2-5]。例如:文献[6]研究了一个与Euler函数φ(n)有关的方程φ(xyz)＝ 2(φ(x)+φ(y)+φ(z))的可解性问题，并给出该方程的所有正整数解。

文献[7]、[8]分别研究了方程 φ(xyz)＝3(φ(x)+φ(y)+φ(z))，φ(xyz)＝4(φ(x)+ φ(y)+φ(z))的可解性问题，并给出该方程的所有正整数解。

本文主要利用初等方法研究不定方程φ(xyz)＝5(φ(x)+φ(y)+φ(z))的可解性，并给出该方程的所有正整数解。即就是

定理:方程

有正整数解:(x，y，z)＝(25，3，3)，(44，3，3)，(50，3，3)，(33，3，4)，(33，4，3)，(25，3，6)，(25，6，3)，(11，3，5)，(22，3，5)，(11，5，3)，(22，5，3)，(11，3，8)，(11，8，3)，(11，3，10)，(11，10，3)，(11，4，5)，(11，5，4)，(11，6，5)，(11，5，6)，(3，3，25)，(3，3，44)，(3，3，50)，(3，4，33)，(4，3，33)，(3，6，25)，(6，3，25)，(3，25，3)，(3，44，3)，(3，50，3)，(3，33，4)，(4，33，3)，(3，25，6)，(6，25，3)，(3，5，11)，(3，5，22)，(3，11，5)，(3，22，5)，(3，8，11)，(3，11，8)，(3，10，11)， (3，11，10)，(4，5，11)，(4，11，5)，(6，5，11)，(6，11，5)，(5，3，11)，(5，3，22)，(5，4，11)，(5，6，11)，(8，3，11)，(10，3，11)，(5，11，3)，(5，22，3)，(5，11，4)，(5，11，6)，(8，11，3)，(10，11，3)。

1 相关引理

引理1.1[6]对任意正整数n，p为素数，则

引理1.2[9]对任意正整数m与n，则

其中(m，n)为m与n的最大公约数。

引理1.3[9]设n是整数，且n≥2，则φ(n)＜n；当n≥3是整数，则φ(n)为偶数。

2 定理的证明

由于φ(xyz)＝5(φ(x)+φ(y)+φ(z))及引理1.2，则有

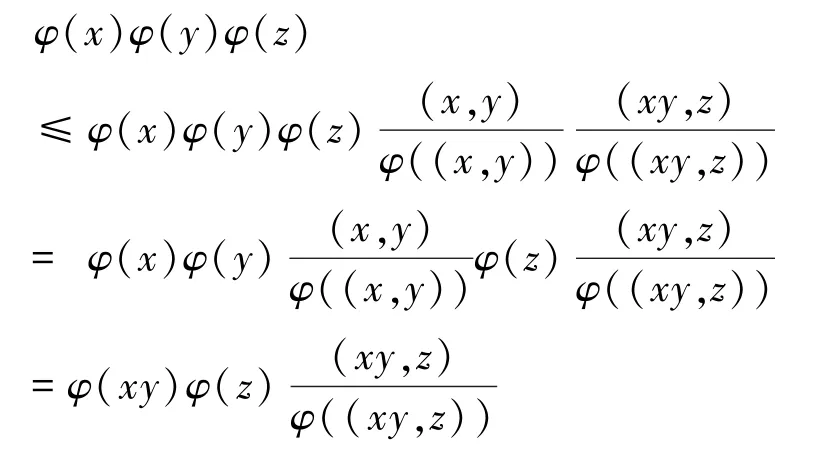
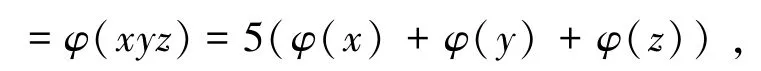
从而有φ(x)φ(y)φ(z)≤5(φ(x)+φ(y)+φ(z))，即

根据φ(y)φ(z)的值，分以下两种情况:

2.1 φ(y)φ(z)≤5

此时φ(y)φ(z)≤4，式(2)成立，则(y，z)＝(1，1)，(1，2)，(1，3)，(1，4)，(1，5)，(1，6)，(1，8)，(1，10)，(1，12)，(2，1)，(2，2)，(2，3)，(2，4)，(2，5)，(2，6)，(2，8)，(2，10)，(2，12)，(3，1)，(3，2)，(3，3)，(3，4)，(3，6)，(4，1)，(4，2)，(4，3)，(4，4)，(4，6)，(5，1)，(5，2)，(6，1)，(6，2)，(6，3)，(6，4)，(8，1)，(8，2)，(10，1)，(10，2)，(12，1)，(12，2)。

显然(y，z)＝(1，1)，(1，2)，(2，1)，(1，3)，(3，1)，(1，4)，(4，1)，(1，5)，(5，1)时，方程(1)无正整数解。

当(y，z)＝(1，6)，(6，1)时，有

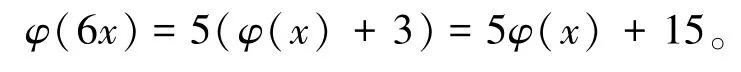
当(y，z)＝(1，8)，(8，1)时，有

当(y，z)＝(1，10)，(10，1)时，有

当(y，z)＝(1，12)，(12，1)时，有

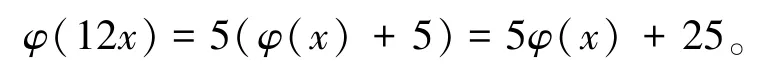
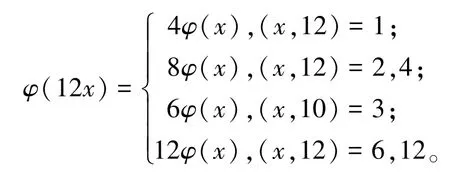
由于由此可知，此时方程(1)无正整数解。

当(y，z)＝(2，2)时，有

当(y，z)＝(2，3)，(3，2)时，有φ(6x)＝5(φ(x)+3)＝5φ(x)+15。根据以上φ(6x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(3，3)时，有

当(y，z)＝(2，4)，(4，2)时，有φ(8x)＝5(φ(x)+3)＝5φ(x)+15。根据以上φ(8x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(2，5)，(5，2)时，有φ(10x)＝5(φ(x)+5)＝5φ(x)+25。根据以上φ(10x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(2，6)，(6，2)时，有φ(12x)＝5(φ(x)+3)＝5φ(x)+15。根据以上φ(12x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(2，8)，(8，2)时，有φ(16x)＝5(φ(x)+5)＝5φ(x)+25。由于

由此可知，此时方程(1)无正整数解。

当(y，z)＝(2，10)，(10，2)时，有φ(20x)＝5(φ(x)+5)＝5φ(x)+25。由于

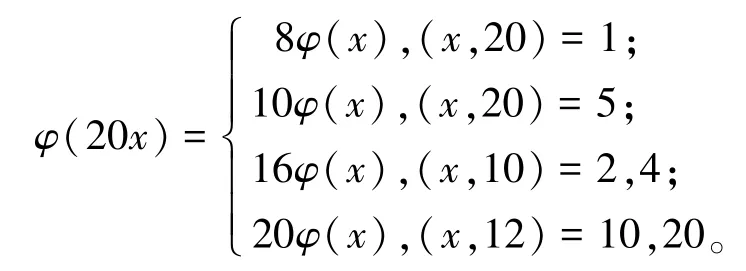
由此可知，此时方程(1)无正整数解。

当(y，z)＝(2，12)，(12，2)时，有φ(24x)＝5(φ(x)+5)＝5φ(x)+25。由于

由此可知，此时方程(1)无正整数解。

当(y，z)＝(3，4)，(4，3)时，有φ(12x)＝5(φ(x)+4)＝5φ(x)+20。根据以上φ(12x)的讨论可知，当6φ(x)＝5φ(x)+20，从而φ(x)＝20，则x＝33。因而方程(1)有正整数解(x，y，z)＝(33，3，4)，(33，4，3)。

当(y，z)＝(3，6)，(6，3)时，有φ(18x)＝5(φ(x)+4)＝5φ(x)+20。由于

此时，当6φ(x)＝5φ(x)+20，从而φ(x)＝20，x＝25。因而方程(1)有正整数解(x，y，z)＝(25，3，6)，(25，6，3)。

当(y，z)＝(4，4)时，有φ(16x)＝5(φ(x)+ 4)＝5φ(x)+20。根据以上φ(16x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(4，6)，(6，4)时，有φ(24x)＝5(φ(x)+4)＝5φ(x)+20。根据以上φ(24x)的讨论可知，此时方程(1)无正整数解。

2.2 φ(y)φ(z)＞5

当φ(y)φ(z)＞5时，此时有φ(y)φ(z)≥6。

(i)当φ(y)φ(z)＝6时，有φ(y)＝1，φ(z)＝6或φ(y)＝6，φ(z)＝1。

当φ(y)＝1，φ(z)＝6时，有y＝1，2；z＝7，9，14，18，则(y，z)＝(1，7)，(1，9)，(1，14)，(1，18)，(2，7)，(2，9)，(2，14)，(2，18)这8种情况。

当(y，z)＝(1，7)时，有φ(7x)＝5(φ(x)+ 7)＝5φ(x)+35。由于

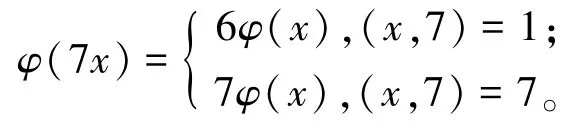
由此可知，此时方程(1)无正整数解。

当(y，z)＝(1，9)时，有φ(9x)＝5(φ(x)+ 7)＝5φ(x)+35。根据以上φ(9x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(1，14)时，有φ(14x)＝5(φ(x)+ 7)＝5φ(x)+35。由于

由此可知，此时方程(1)无正整数解。

当(y，z)＝(1，18)时，有φ(18x)＝5(φ(x)+ 7)＝5φ(x)+35。根据以上φ(18x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(2，7)时，有φ(14x)＝5(φ(x)+ 7)＝5φ(x)+35。根据以上φ(14x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(2，9)时，有φ(18x)＝5(φ(x)+ 7)＝5φ(x)+35。根据以上φ(18x)的讨论可知，此时方程(1)无正整数解。

当(y，z)＝(2，14)时，有φ(28x)＝5(φ(x)+ 7)＝5φ(x)+35。由于

由此可知，此时方程(1)无正整数解。

当(y，z)＝(2，18)时，有φ(36x)＝5(φ(x)+ 7)＝5φ(x)+35。由于

由此可知，此时方程(1)无正整数解。

同理当φ(y)＝6，φ(z)＝1时，方程(1)无正整数解。

(ii)当φ(y)φ(z)＝8时，有φ(y)＝1，φ(z)＝8或φ(y)＝ 2，φ(z)＝ 4或φ(y)＝ 4，φ(z)＝ 2或φ(y)＝ 8，φ(z)＝1。当φ(y)＝1，φ(z)＝8时，有y＝1，2；z＝15，16，20，24，30。当φ(y)＝ 2，φ(z)＝4时，有y＝3，4，6；z＝5，8，10，12。仿φ(y)φ(z)＝6情况讨论可得，此时方程(1)有正整数解(x，y，z)＝(11，3，5)，(22，3，5)，(11，3，8)，(11，3，10)，(11，4，5)，(11，6，5)，(11，5，3)，(22，5，3)，(11，8，3)，(11，10，3)，(11，5，4)，(11，5，6)。

(iii)当φ(y)φ(z)＝10时，有φ(y)＝1，φ(z)＝10或φ(y)＝10，φ(z)＝1。当φ(y)＝1，φ(z)＝10时，有y＝1，2；z＝11，22。仿φ(y)φ(z)＝6情况讨论可得，此时方程(1)无正整数解。

(iv)当φ(y)φ(z)＝ 12时，有φ(y)＝ 1，φ(z)＝12或φ(y)＝2，φ(z)＝6或φ(y)＝6，φ(z)＝2或φ(y)＝12，φ(z)＝1。当φ(y)＝1，φ(z)＝12时，y＝1，2；z＝13，21，26，28，36，42。当φ(y)＝2，φ(z)＝6时，y＝3，4，6；z＝7，9，14，18。仿φ(y)φ(z)＝6情况讨论可得，此时方程(1)有正整数解。

(v)当φ(y)φ(z)≥14时，由于φ(y)，φ(z)均为正整数，所以有(φ(y)-1)(φ(z)-1)≥0及φ(y)φ(z)+1≥φ(y)+φ(z)。由(2)有

所以φ(x)＝1，2，4，6，8。

①若φ(x)＝1时，φ(y)φ(z)＝φ(x)φ(y)φ(z)≤φ(xyz)＝5(1+φ(y)+φ(z))。 于是有

(φ(y)-5)(φ(z)-5)≤30。

当(φ(y)-5)(φ(z)-5)＜0时，若φ(y)＝1，则φ(z)≥6，此时直接验证可知方程(1)无解。同理若φ(z)＝1，则φ(y)≥6方程(1)无解；若φ(y)＝2，则φ(z)≥6，此时直接验证可知方程(1)无解。同理若φ(z)＝2，则φ(y)≥6方程(1)无解；若φ(y)＝4，则φ(z)≥6，此时直接验证可知方程(1)无解。同理若φ(z)＝4，则φ(y)≥6方程(1)无解。

当(φ(y)-5)(φ(z)-5)＝0时，则φ(y)，φ(z)至少有一个等于5，此时方程(1)无解。

当(φ(y)-5)(φ(z)-5)＝1时，有φ(y)＝6，φ(z)＝6或φ(y)＝4，φ(z)＝4。此时5(1+ φ(y)+φ(z))均为奇数。因而方程(1)无正整数解。

当(φ(y)-5)(φ(z)-5)＝2时，有φ(y)＝6，φ(z)＝7或φ(y)＝7，φ(z)＝6或φ(y)＝4，φ(z)＝3或φ(y)＝3，φ(z)＝4。此时φ(y)，φ(z)中有一个不成立，因而方程(1)无正整数解。

当(φ(y)-5)(φ(z)-5)＝3时，有φ(y)＝8，φ(z)＝6或φ(y)＝6，φ(z)＝8或φ(y)＝2，φ(z)＝4或φ(y)＝4，φ(z)＝2。此时5(1+φ(y)+ φ(z))均为奇数。因而方程(1)无正整数解。

当(φ(y)-5)(φ(z)-5)＝4时，有φ(y)＝6，φ(z)＝9或φ(y)＝9，φ(z)＝6或φ(y)＝7，φ(z)＝7或φ(y)＝1，φ(z)＝4或φ(y)＝4，φ(z)＝1或φ(y)＝3，φ(z)＝3。验证不成立，因而方程(1)无正整数解。

当(φ(y)-5)(φ(z)-5)＝5，7，9，11，13，15，17，19，21，23，25，27，29时，5(1+φ(y)+φ(z))均为奇数。因而方程(1)无正整数解。

当(φ(y)-5)(φ(z)-5)＝6，8，10，12，14，16，18，20，22，24，26，28，30时，φ(y)，φ(z)中至少有一个不成立，因而方程(1)无正整数解。

②若φ(x)＝2时，此时有

2φ(y)φ(z)＝φ(x)φ(y)φ(z)≤ φ(xyz)＝5(2+φ(y)+φ(z))＜6(2+φ(y)+φ(z))。于是有(φ(y)-3)(φ(z)-3)＜15。

当(φ(y)-3)(φ(z)-3)＜0时，若φ(y)＝1，则φ(z)≥4，此时有x＝3，4，6；y＝1，2。因而方程(1)无正整数解。同理若φ(z)＝1，则φ(y)≥4方程(1)无解；若φ(y)＝2，则φ(z)≥4，此时有x＝3，4，6；y＝3，4，6。因而方程(1)有正整数解(3，3，25)，(3，3，44)，(3，3，50)，(3，4，33)，(4，3，33)，(3，6，25)，(6，3，25)。同理若φ(z)＝2，则φ(y)≥4时，因而方程(1)有正整数解(3，25，3)，(3，44，3)，(3，50，3)，(3，33，4)，(4，33，3)，(3，25，6)，(6，25，3)。

当(φ(y)-3)(φ(z)-3)＝0时，φ(y)，φ(z)中至少有一个等于3，因而方程(1)无正整数解。

当(φ(y)-3)(φ(z)-3)＝1，2，3，4，5，9，11，13时，通过验证不成立，因而方程(1)无正整数解。

当(φ(y)-3)(φ(z)-3)＝7时，有φ(y)＝4，φ(z)＝10或φ(y)＝10，φ(z)＝4。因而方程(1)有正整数解(3，5，11)，(3，5，22)，(3，11，5)，(3，22，5)，(3，8，11)，(3，11，8)，(3，10，11)，(3，11，10)，(4，5，11)，(4，11，5)，(6，5，11)，(6，11，5)。

当(φ(y)-3)(φ(z)-3)＝6，8，10，12，14时，φ(y)，φ(z)中至少有一个不成立，因而方程(1)无正整数解。

③若φ(x)＝4时，此时有

4φ(y)φ(z)＝φ(x)φ(y)φ(z)≤ φ(xyz)＝5(4+φ(y)+φ(z))＜8(4+φ(y)+φ(z))。于是有(φ(y)-2)(φ(z)-2)＜12。

当(φ(y)-2)(φ(z)-2)＜0时，若φ(y)＝1，则φ(z)≥4，通过验证不成立，因而方程(1)无正整数解。同理若φ(z)＝1，则φ(y)≥4，方程(1)无正整数解。

当(φ(y)-2)(φ(z)-2)＝0时，则φ(y)，φ(z)中至少有一个等于2。当φ(y)＝2时，方程(1)有正整数解(5，3，11)，(5，3，22)，(5，4，11)，(5，6，11)，(8，3，11)，(10，3，11)。同理当φ(z)＝2时，方程(1)有正整数解(5，11，3)，(5，22，3)，(5，11，4)，(5，11，6)，(8，11，3)，(10，11，3)。

当(φ(y)-2)(φ(z)-2)＝1，4，8时，通过验证不成立，因而方程(1)无正整数解。

当(φ(y)-2)(φ(z)-2)＝2，3，5，6，7，9，10，11时，φ(y)，φ(z)中至少有一个不成立，因而方程(1)无正整数解。

④若φ(x)＝6时，此时有

6φ(y)φ(z)＝φ(x)φ(y)φ(z)≤ φ(xyz)＝5(6+φ(y)+φ(z))＜6(6+φ(y)+φ(z))。于是有0≤(φ(y)-1)(φ(z)-1)＜7。

当(φ(y)-1)(φ(z)-1)＝0，1，3，5时，通过验证不成立，因而方程(1)无正整数解。

当(φ(y)-1)(φ(z)-1)＝2，4，6时，φ(y)，φ(z)中至少有一个不成立，因而方程(1)无正整数解。

⑤若φ(x)＝8时，此时有

8φ(y)φ(z)＝φ(x)φ(y)φ(z)≤ φ(xyz)＝5(8+φ(y)+φ(z))＜8(8+φ(y)+φ(z))。于是有0≤(φ(y)-1)(φ(z)-1)＜9。

当(φ(y)-1)(φ(z)-1)＝0，1，3，5，7时，通过验证不成立，因而方程(1)无正整数解。

当 (φ(y)-1)(φ(z)-1)＝2，4，6，8时，φ(y)，φ(z)中至少有一个不成立，因而方程(1)无正整数解。

[1]Tom M.Apostol.Introduction to analytic number theory[M].New York:Spring-Verlag，1976.

[2]Guy R.K.Unsolved Problem in Number Theory[M].Third edition. New York:Springer-Verlag，2004.

[3]El-Kassar N.on the equations kφ(n)＝φ(n+1)and kφ(n+1)＝φ(n)，Number Theory and related topics(Seoul 1998)95-109，Yonsei Univ Inst Math Sci，Seoul 2000.

[4]陈国慧.一个包含Euler函数的方程[J].纯粹数学与应用数学，2007，23(4):439-445.

[5]Sun Cuifang，Cheng Zhi.Some Kind of Equation Involving Euler Functionφ(n)[J].数学研究，2010，4(43):364-369.

[6]孙翠芳，程智.关于方程φ(xyz)＝2(φ(x)+φ(y)+φ(z)) [J].数学的实践与认识，2012，42(23):267-271.

[7]张四保，杜先存.一个包含Euler函数方程的正整数解[J].华中师范大学学报(自然科学版)，2015，49(4):497-501.

[8]张四保.不定方程φ(xyz)＝4(φ(x)+φ(y)+φ(z))的解[J].东北石油大学学报，2013，37(6):113-118.

[9]Rosen K H.Elementary number theory and its applications[M]. Fifth edition.Addison:Wesley，Pearson Education，Inc.，2005.

(责任编辑:曾 晶)

The Positive Integer Solution of an Equation Involving the Euler Function

WANG Xihan，GAO Li∗，LUWeiyang

(College of Mathematics and Computer Science，Yan’an University，Yan’an 716000，China)

For any positive integer n，φ(n)is Euler function.That is the number of all positive integers not exceeding n which are relatively prime to n.Themain purpose of this paper is to study the solutions of the equation φ(xyz)＝5(φ(x)+(φ(y)+(φ(z))，and gives all its solution.

Euler function；Diophantine equation；positive integer solutions

O156

A

1000-5269(2016)04-0025-05

10.15958/j.cnki.gdxbzrb.2016.04.05

2016-05-04

陕西省科技厅科学技术研究发展计划项目(2013JQ1019)；延安大学校级科研计划项目—引导项目(YD2014-05)；延安大学研究生教育创新计划项目

王曦浛(1990-)，女，在读硕士，研究方向:数论，Email:648034259＠qq.com.

∗通讯作者:高丽，Email:yadxgl＠163.com.