铁路行包运输网络拓扑结构分析

张文斌

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

铁路行包运输网络拓扑结构分析

张文斌

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

在阐述平均路径长度、聚类系数和度与度分布3个主要复杂网络统计参数的基础上，从平均路径长度及节点距离与节点对数、度与度分布、聚类系数3个方面分析铁路行包快运网的网络结构特性，对行包运输网络和地理网络的统计属性进行相应的比较分析。研究表明，利用复杂网络的方法对行包运输网络进行研究和规划具有一定借鉴意义。

行包运输；网络拓扑结构；复杂网络

近年来，随着快递运输公司的发展，快运市场份额被迅速抢占，铁路行包运输量逐年下降[1]。面对来自快运市场的压力，针对行包运输市场现状及行包运输网络系统特性，铁路应完善网络节点布局，全面规划行包运输网络[2-3]。目前国内学者对行包运输网络进行了诸多研究，刘坤[4]运用节点重要度计算和节点聚类分析的方法对行包运输网络进行规划，并提出当节点较复杂时进行行包运输网络规划的方法；余朵苟[5]利用复杂网络的基本理论和方法，从数学拓扑和物理网络结构的角度分析快运网络；周漩等[6]人对确定复杂网络关键节点进行研究；武云霞[7]采用复杂网络的统计参数对快运网络的特性和功能进行理论分析。基于上述研究，在复杂网络的基础上，以行包快运列车停靠站点和运输径路构建运输网络，以行包快运列车停靠站点和铁路线路构建地理网络。通过计算和分析行包运输网络和地理网络统计参数，比较二者之间的差异，为我国行包运输网络规划研究提供参考。

1 复杂网络统计参数

复杂网络涉及很多统计参数，但最主要的 3 个参数为平均路径长度、聚类系数和度与度分布[8]。

1.1 平均路径长度

假设铁路网无权重和方向，因而 2 个车站 i，j 之间的最短路径是指连接这 2 个车站的线路边数最少的路径。定义 dij为连接着这 2 个站点最短距离的所有不同线路边数目。将铁路网中任意不同 2 个车站之间的最大距离长度称为铁路网直径，记为 D，计算公式为[7]

定义运输网和地理网的平均路径长度 L 为任意 2个车站之间距离的平均值，计算公式为[7]

其中，⑵ 式包含车站自身的距离；N 为所有节点数目。如果不考虑站点自身的距离，则节点数应由 N变为 (N－1)，计算公式为[7]

1.2 聚类系数

通常假设 1 个铁路网中的车站 i 有 ki条铁路线路将其与其他车站相连接，即车站 i 有 ki个直接有线路相连接的邻居站点 (复杂网络中简称邻居或邻节点)。如果车站 i 的 ki个邻居站点之间也相邻，则在这些车站之间存在 ki(ki－1) / 2 条相连线路，这是线路数最多的一种情形。但是，在实际铁路网中，车站 i 的 ki个邻节点之间未必都互为邻居，因而假设 ki个车站之间实际相互连接的铁路线路数目为 Ei，其与总可能存在边数 ki( ki－1) / 2 之间的比值为车站聚类系数 Ci，计算公式为[9]

网络的聚类系数 C 即为 Ci的平均值，计算公式为[10]

式中：N 为所有节点数目； 0≤C≤1。

1.3 度与度分布

上述铁路运输网和地理网中车站 i 的度 ki为与该站直接相连的铁路线路条数，所有车站站点的度的平均值称为平均度，记作 k。如果将铁路网中站点的度按照从大到小进行排序，可以得到度为 k 的站点占整个站点数的比例 Pk，即铁路网中随机选择站点的度为k 的概率 (度分布)。

2 铁路行包快运网的网络结构特性分析

根据现行的铁路行包开行方案，在具体装卸站点和行包运行径路[11]的基础上构建行包运输网络；不考虑开行方案中具体的运行径路，只考虑站点之间线路的连接，以此建立地理网络。基于复杂网络分析软件 Pajek 算法的优越性、强大的导出及可视化功能，在参数计算时，利用 Pajek 软件对需要分析的节点进行编号，然后建立节点之间的邻接矩阵，以 .mat 的文件格式保存邻接矩阵，最后将文件导入 Pajek 软件中进行参数计算。

2.1 平均路径长度

以铁路行包运输网络为例，主要分析其重要的121 个行包装卸站点，利用 Pajek 计算得到运输网络平均路径长度为 10.183 47，即任意 2 个站之间相互运输需要经过 10～11 次中转，说明运输网络上任意 2 个节点之间的距离较大，行包运输效率较低。因此，建议适当增加行包的作业站点，提高行包运输的可达性；完善行包运输网络节点的规划，以减少中转次数，提高行包运输效率。平均路径长度 (L) 的大小表示网络全局效率的高低，L 越小，表明从 1 个节点到另一个节点的中转次数越少，则所用的时间成本和距离成本越小，网络效率越高。地理网络平均路径长度为 6.771 90，说明从网络中一个节点到任意一个节点需要进行 6～7 次中转，即在实际地理网络运输中从 1 个节点到另一个节点的中转次数为 6～7 次，中转次数越少，则表明所用的时间成本和距离成本越小，网络效率越高。运输网络和地理网络节点的距离分布如图 1 所示。

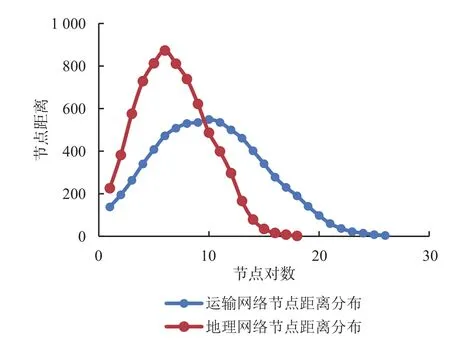
图1 行包运输网络和地理网络节点的距离分布图

其中，横轴为节点对数，纵轴为节点距离。从图 1 中可知，运输网络和地理网络节点的距离服从泊松分布。

2.2 度与度分布

网络的度分布与其拓扑结构紧密相关[12]，车站站点的度表示与该车站直接相连的线路数，站点的度越大，说明在整个网络中连接该车站的线路越多，也说明在整个铁路线路网中该车站的重要度越高。采用Pajek 软件计算得到运输网络的节点平均度为 2.28，地理网络的节点平均度为 3.74。在运输网络中，节点度最大为 5，最小为 1，在 121 个节点中节点度为 2的站点有 80 个，约占比例为 65%，说明在运输网络中 65% 左右的节点与另外 2 个节点相连，符合网络实际情况。在地理网络中，节点中的所有度中最大为 14，最小为 1，在 121 个节点中节点度为 2 的站点有 48 个，约占比例为 40%，节点度为 3 的站点有 25个，约占比例为 21%，说明在行包快运服务网所依托的地理网络中，40% 的节点与另外 2 个节点相互连接，21% 的节点与另外 3 个节点相互连接。行包运输网络和地理网络的节点度分布如图 2 所示。

2.3 聚类系数

站点的聚类系数 (C) 越大，表示整个铁路网中与该站点相连的站点间相互连接的概率也越大。网络的聚类系数是网络中节点聚类系数的平均值，反映网络的聚类特征。网络聚类系数越大，表明网络的聚类程度越高，同时网络小片区域之间更容易形成小的运输网络，方便不同区域之间进行货物集结和疏散，使网络之间的内部协调更加方便。网络的 C 值可以反映网络的拓扑结构特性，C 值越大，说明网络节点之间的连接概率越高，网络越稳定，即 C 越大，网络的抗毁性能也越高[13]。利用 Pajek 计算该运输网络的C = 0.057 97，C 值很小，表明行包运输网络中各站点之间的相互联系并不十分紧密。地理网络的聚类系数为 0.583 95，与运输网络相比，节点之间相互连接的概率较大，具有较好的聚类特征。

图2 行包运输网络和地理网络节点度分布图

2.4 行包运输网络与地理网络属性比较

以行包快运为研究对象，分别计算运输网络和地理网络的平均路径长度、网络直径、节点度与度分布、聚类系数等参数，基本属性相关数值的比较如表 1 所示。

表1 运输网络和地理网络基本属性比较

由表 1 可知，行包运输网络中边的数目比地理网络少，说明行包运输径路并没有覆盖全部的铁路运输线路，可以考虑在后期随着快运市场的发展适当增开行包列车。运输网络平均路径长度和网络直径比地理网络大，也符合实际情况，表明行包运输的径路选择仍然比较单一，而在地理网络中运输线路的选择比较灵活，随着快运市场的发展可以考虑灵活选择运输径路开行行包列车。地理网络的平均度比运输网络大，说明在地理网络中单个节点衔接的线路比运输网络多，一个节点可以选择的运输路径也较多，路线的选择较灵活，符合二者自身的网络聚类特征。地理网络的 C 值为 0.583 95，说明该网络的局部站点密度较大，节点之间相互连接的概率大，具有较好的聚类特征，而在行包运输网络中反映不出该聚类特征，因而建议适当增加行包的作业站点，提高行包运输的可达性及站点密集度。

3 结束语

铁路行包货物运输作为铁路运输的重要组成部分，行包运输网络结构对提高行包运输的能力和效率具有重要意义。通过构建我国铁路行包运输网络及其地理网络的网络拓扑结构和分析这 2 个网络的平均路径长度、聚类系数及度与度分布等统计参数的计算结果表明，行包运输网络的平均路径长度比地理网络大，运输网络的节点连接并不十分紧密。由于在构建快捷货物运输网络和地理网络时主要选取的站点有限，随着铁路货运组织改革的推进，将进一步完善行包运输网络，通过采用系统动力学方法结合具体车流对行包运输网络进行动态分析和研究。

[1] 张瑞荣. 当前铁路行包运输存在问题分析及对策[J]. 上海铁道科技， 2014(4)：139-140.

[2] 魏 然，张国平. 加快发展铁路行包大列运输的思考[J]. 铁道运输与经济，2009，31(7)：9-11. WEI Ran，ZHANG Guo-ping. Thoughts on Accelerating the Development of Railway Baggage & Parcel Special Train[J]. Railway Transport and Economy，2009，31(7)：9-11.

[3] 王国东. 铁路行包运输组织方法及其优化研究[J]. 科技与企业，2012 (16)：88.

[4] 刘 坤. 铁路行包快运服务网络规划及设计研究[D]. 兰州：兰州交通大学，2014.

[5] 余朵苟. 基于复杂网络理论的快捷货运网络拓扑结构研究[D]. 北京：北京交通大学，2009.

[6] 周 漩，张凤鸣，李克武，等. 利用重要度评价矩阵确定复杂网络关键节点[J]. 物理学报，2012，61(5)：1-7. ZHOU Xuan，ZHANG Feng-ming，LI Ke-wu，et al. Finding Vital Node by Node Importance Evaluation Matrix in Complex Networks[J]. Acta Physica Sinica，2012，61(5)：1-7.

[7] 武云霞. 基于复杂网络的综合快捷货运服务网络结构研究[D]. 北京：北京交通大学，2010.

[8] 赵 月，杜 文，陈 爽. 复杂网络理论在城市交通网络分析中的应用[J]. 城市交通，2009 (1)：57-65. ZHAO Yue ，DU Wen，CHEN Shuang. Application of Complex Network Theory to Urban Transportation Network Analysis[J]. Urban Transport of China，2009 (1)：57-65.

[9] 武云霞，何世伟. 综合运输体系下快捷货运服务网络结构影响因素分析[J]. 物流科技，2009，32(8)：29-33. WU Yun-xia，HE Shi-wei. Analysis of Network Structure Factors for Express Multimodal Freight TransportationService Network[J]. Logistics Sci-Tech，2009，32(8)：29-33.

[10] 汪小帆，李 翔，陈关荣. 复杂网络理论及其应用[M].北京：高等教育出版社，2012：97-98.

[11] 快运货物班列[EB/OL]. (2015-05-31)[2015-08-01]. http://hyfw.95306.cn/hyinfo/page/home-hyzx-blky.

[12] 王 林，戴冠中. 复杂网络的度分布研究[J]. 西北工业大学学报，2006，24(4)：405-409. WANG Lin，DAI Guan-zhong. On Degree Distribution of Complex Network[J]. Journal of Northwestern Polytechnical University，2006，24(4)：405-409.

[13] 彭兴钊，姚 宏，丁 超，等. 变聚类系数加权网络的建模及其级联抗毁性分析[J]. 系统工程与电子技术，2014(12)：2449-2455. PENG Xing-zhao，YAO Hong，DING Chao，et al. Modeling of Weighted Network with Tunable Clustering and Cascading Invulnerability Analyses[J]. Systems Engineering and Electronics，2014(12)：2449-2455.

责任编辑： 吴文娟

Analysis on Network Topology of Railway Luggage Transportation

ZHANG Wen-bin

(School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, Gansu, China)

Based on expounding 3 major statistic parameters of sophisticated network like average path length, clustering coefficient and degree-degree distribution, this paper analyzes the structure properties of railway luggage express network from 3 aspects including average path length (contains distance between nodes and node logarithm), degree and degree distribution as well as clustering coefficient, and makes comparative analysis on the statistic properties of luggage transport network and geographical network. The study result shows the analysis and planning of luggage transport network by using sophisticated network have certain signification for reference.

Luggage Transportation; Network Topology; Sophisticated Network

1004-2024(2016)01-0046-04

U294.1+5

A

10.16669/j.cnki.issn.1004-2024.2016.01.10

2015-08-26

兰州市社科规划项目 (15-039D)