浅谈高中物理教学中动能定理解题技巧

潘佳萍●

江苏苏州青云实验中学(210230)



浅谈高中物理教学中动能定理解题技巧

潘佳萍●

江苏苏州青云实验中学(210230)

动能定理是高中物理的核心内容，涉及到运动学和力学知识，合理利用动能定理不仅能够简化解题过程，更能够帮助学生从能量转移、外力做功等角度理解物理过程，进而有效提升物理解题技能.本文基于动能定理的适用范围、应用条件，剖析了动能定理在解题中的优势以及误用等.

动能定理;高中物理; 合外力;能量守恒

一、动能定理的适用范围以及使用条件

动能定理的物理定义表明，该物理量体现了能量的变化量，属于标量类型，反应了物体动能的变化以及引起动能变化的原因.外力对物体做正功，物体动能增加；反之，物体克服外力做功，亦即外力做负功时，物体的动能减小，该因果关系不仅体现了力是改变物体状态的原因，同时也表明做功时能量变化的原因之一.

从使用范围以及应用条件的角度来讲，动能定理用于独立的研究对象，对于系统而言，由于涉及到内力作用等因素，因此不符合动能定理适用范围，可见动能定理所体现的能量变化仅属于动能的变化，不考虑内能等其他形式的能量转移.

力的独立作用原理决定了动能定理的求解呈现多元化，可以采用合力的做功求解，也可以采用不同单个分力的做功之和求解，从求解角度来讲，动能定理源于对直线运动模型的推导，然而基于该原理所体现的真实物理模型，同样适用于曲线运动以及变速运动模型，因此具有相对较广的使用范围.

二、动能定理解题技巧分析

1.利用动能定理解决变力做功问题

通常情况下，采用牛顿第二定律和相关运动学能够解决的物理学问题都能用动能定理进行求解，相比，动能定理具有更加简洁的求解过程，不仅如此，从物理过程的思考角度来讲，动能定理的所需要的物理思维更加容易掌握，最常见的就是利用动能定理可以忽略物体过程的变化，如变力做功问题以及运动轨迹的变化问题等.

例如，质量为m的木块与细线连接固定在光滑水平台面上，已知当通过细线作用力的大小为F时，木块在水平台面上恰好做圆周运动，其半径为R.如果将作用力从F减小为原来的1/6时，该木块能够继续做匀速圆周运动，然而其运动半径为原来的3倍，试问，在此过程中通过细线的作用力做功多少？

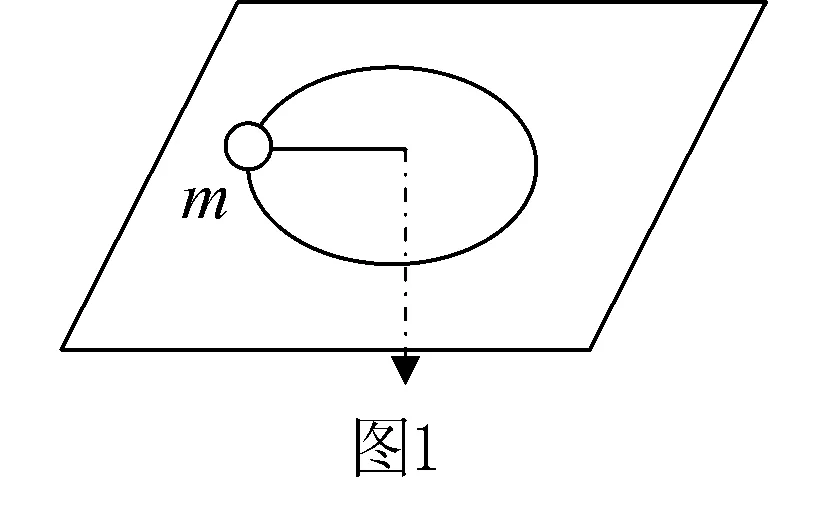
分析 该过程是典型的变力做功问题，作用力由F减小为原来的1/6时，使得木块做圆周运动的向心力减小，导致运动半径增加.如果采用牛顿第二定律以及圆周运动公式求解，很难找到突破口，而且该变化过程中作用力的方向在不断发生变化，因此该情况下若采用动能定理，可以忽视作用力在该过程中的具体变化行为，仅围绕物体初始和末了状态的动能进行求解即可.

求解：首先确定初始状态和最终状态物体m所具有的动能E1和E2： 则根据动能定理，该过程拉力做功可以表示为：E2-E1即可.进而根据初始状态拉力产生的向心力与运动速度、半径之间满足的运动学方程：联合求解.可见，本题中采用了动能定理后极大程度上简化了物理过程，仅考虑了两个特征状态的动能，较为简单地得到了变力在物理过程中的做功情况.

2.利用动能定理解决相对位移问题

动能定理的优越性除了能够解决变力问题时，在具有复杂相对位移的模型中也能体现出其解题的简易性.然而该模型中对相对位移的选取参考系必须具有统一性，这也是动能定理应用中的劣势之一，需要对研究对象进行系统划分，通常对于位移的研究，选取惯性系模型，以及选用地球为参考系，来判断系统内不同研究对象所经历的实际位移.

例如，在水平地面上静止一个质量为M的木板，现有一个子弹以速度v1从左到右进入木板，经过时间t以后，子弹从木板右侧传出，此时木子弹相对地面的速度为v2，已知子弹的质量为m，木板与水平面间的摩擦因数是μ，试求该过程中木板的位移？

分析 子弹进入木板以后，由于彼此摩擦力的存在，使得木板受到子弹施加的向右摩擦力f1与地面施加的向左的摩擦力f2，同时子弹受到向左的摩擦阻力-f1.计算木板的位移必须以地面为参考系，考虑其初始位置和最终状态的能量变化.显然，如果采用传统运动学公式，很难直接得到木板位移.由于木板在该过程中受到两个摩擦力的作用，因此其动能的变化等于合外力所做的功，如果采用动能定理考虑木板两个特殊状态的动能变化，即可轻松得到木板在该合外力下所移动的距离.对于子弹而言，可根据在木板内部行进的时间t采用动量公式求出其内部摩擦力f1的大小：f1t=mV2-mV1,同样，根据动量关系求出木板受到的合外力的大小：(f2-f1)t=μ(M+m)g，由此可得到木板的末了状态速度Vt，最后根据动能定理公式，木板动能的变化量即为合外力所做的功： ,联合可求得位移s的大小.

动能定理是高中物理学的核心内容，也体现了力与做功之间的因果关系，适当利用动能定理能够有效简化解题过程.然而动能定理具有其特殊的应用条件，亦即主要考虑单个对象的动能变化与做功关系，其优势在于能够处理复杂系统中物体的位移问题、变力做功问题等.

[1]莉莲；浅析高中动能定理教学新思路[J]；中学生导报，2014(10).

[2]陈佳佳；高中物理教学模式漫谈[J]；中学课程辅导，2014(05)

G632

B

1008-0333(2016)28-0067-01