求函数解析式的非常规武器

南京市大厂高级中学(210044)

雷亚庆●



求函数解析式的非常规武器

南京市大厂高级中学(210044)

雷亚庆●

求函数解析式的常规方法主要是待定系数法和换元法，但是有时这些常规方法派不上用场，这时我们就需要掌握一些非常规武器来解决问题.下分别举例说明.

一、配凑法

指的是用配凑(如配方，拼凑)的手段得到函数解析式的方法

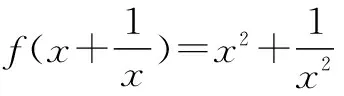
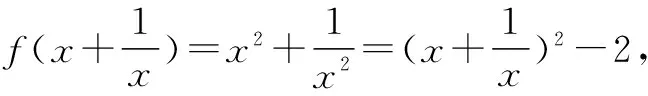
所以f(x)=x2-2(x≤-2或x≥2).

例2 已知函数f(x)满足：f(sinx)=cos2x，求f(x).

解f(sinx)=1-sin2x,

所以f(x)=1-x2(-1≤x≤1).

解题反思 上述例题如果直接用换元法求解时会遇到不好用所换元表示原有元的问题，这时配凑法就可以大显身手了，但是配凑时要注意保证定义域的准确性

二、利用对偶式

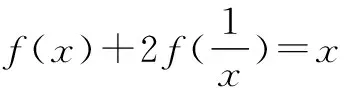
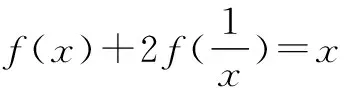
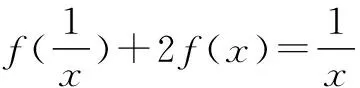
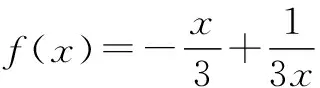
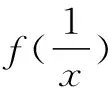
三、利用奇偶性

例4 已知函数f(x)为奇函数，g(x)为偶函数,且f(x)+g(x)=x3+x2+1, 求f(x).

解 因为f(x)+g(x)=x3+x2+1 ①,

所以有f(-x)+g(-x)=-x3+x2+1 ②.

又因为f(x)为奇函数，g(x)为偶函数,

所以得-f(x)+g(x)=-x3+x2+1 ③.

①-③得： 2f(x)=2x3. 所以f(x)=x3.

解题反思 利用奇偶性，构造类似例3的对偶式使问题得解

例5 已知函数f(x)为定义在R上的奇函数，且x<0时，f(x)=lg(1-x),求f(x)的解析式.

解 因为函数f(x)为定义在R上的奇函数,所以f(0)=0.且x>0时，-x<0,f(x)=-f(-x)=-lg(1+x).

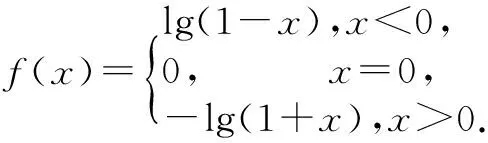
解题反思 利用奇偶性可以把所求区间转化到已知的对称区间，利用已知区间的解析式求出所求区间的解析式.

四、利用对称

1.利用轴(直线)对称

例6 求与函数f(x)=x2-2x图象关于直线x=2对称的函数g(x)的解析式.

解析 点P(x,y)为函数g(x)图象上任意一点，则点P关于直线x=2对称的点的坐标为P′(4-x,y).

由题意点P′(4-x,y)在函数f(x)=x2-2x的图象上,

所以y=(4-x)2-2(4-x), 即y=x2-6x+8.

所以g(x)=x2-6x+8.

解题反思 实际上我们可以把问题一般化得到如下结论：与函数y=f(x)图象关于直线x=a对称的函数为y=f(2a-x).

2.利用中心(点)对称

例7 求与函数f(x)=x2-2x图象关于直线(2,1)对称的函数g(x)的解析式.

解析 点P(x,y)为函数g(x)图象上任意一点，则点P关于点(2，1)对称的点的坐标为P′(4-x,2-y).

由题意点P′(4-x,2-y)在函数f(x)=x2-2x的图象上，所以2-y=(4-x)2-2(4-x), 即y=-x2+6x-6.

所以g(x)=-x2+6x-6.

解题反思 实际上我们也可以把问题一般化得到如下结论：与函数y=f(x)图象关于点(a,b)对称的函数为：y=2b-f(2a-x).

五、利用周期性

例8 已知函数f(x)满足f(x+4)=f(x)，且0≤x≤1时f(x)=x2，求x∈[4,5]时，函数f(x)的解析式.

解析 由f(x+4)=f(x)可知函数f(x)是周期函数，4是它的一个周期, 所以x∈[4,5]时，x-4∈[0,1],f(x)=f(x-4)=(x-4)2.

解题反思 利用周期把所求区间退回到已知区间使问题得解.

六、利用递推关系

例9 已知函数f(x)满足f(x+1)=2f(x)，且0≤x≤1时f(x)=x2，求x∈[-3,-2]时，函数f(x)的解析式.

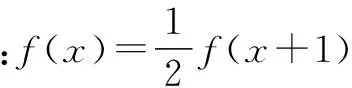
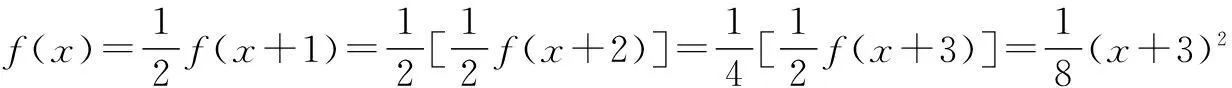
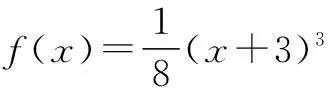
解题反思 利用递推关系将所求区间一步一步转化到已知区间，利用已知区间的解析式求出所求区间上的解析式，使问题顺利解决.

G632

B

1008-0333(2016)22-0033-01