一道向量题的解法研究

云南省蒙自市蒙自一中(新校区)(661100)

苏保明●



一道向量题的解法研究

云南省蒙自市蒙自一中(新校区)(661100)

苏保明●

平面向量是高考命题的重要内容之一，常以填空题或选择题呈现.由于高考向量题内容新颖、解法众多，导致同学们有时难以入手.为了帮助同学们更好掌握解题思路和方法，现举一例剖析如下.

题目 已知a,b是单位向量，a·b=0.若向量c满足|c-a-b|=1，则|c|的取值范围是( ).

此题是一道具有很强的灵活性与挑战性的名题，虽然题目的表达简洁平淡，却给人以轻车熟路之感.

方法一 利用公式x2+y2≥2xy

解法1 由题意可知，向量a、b是一对单位正交基底，所以建立平面直角坐标系xOy，并设a=(1,0),b=(0,1),c=(x,y)，则c-a-b=(x-1,y-1).

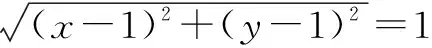
因为x2+y2≥2xy，所以2(x2+y2)≥x2+2xy+y2=(x+y)2，

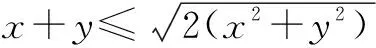
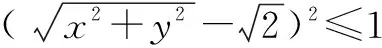
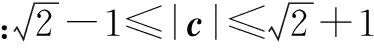
解法2 由解法1知，2(x+y)=x2+y2+1.

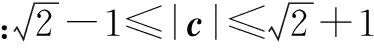
方法三：三角法

设x-1=cosα,y-1=sinα，其中α∈R，则x=1+cosα，y=1+sinα.

所以x2+y2=(1+cosα)2+(1+sinα)2

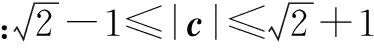
评注 由(x-1)2+(y-1)2=1联想到公式sin2α+cos2α=1，故设x-1=cosα，y-1=sinα.本题通过构造三角函数，把较为复杂的代数问题转化为简单的三角问题，从而利用三角函数的有界性求出|c|的取值范围.

方法四 向量法

解法4 由解法1知2(x+y)=x2+y2+1.

设m=(x,y),n=(1,1)，则由m·n≤|m||n|得

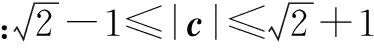
方法五：柯西不等式法

解法5 由解法1知2(x+y)=x2+y2+1，

根据柯西不等式，得

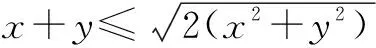
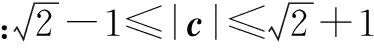
方法六：构造圆

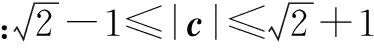
如图1，因为圆(x-1)2+(y-1)2=1与圆x2+y2=R2有公共点，

方法七 利用EX2≥(EX)2

解法8 由解法1知2(x+y)=x2+y2+1，

构造离散型随机变量X的分布列：

XxyP1212

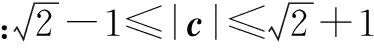
评注 用此法解决问题的关键就是正确构造离散型随机变量的分布列，能使EX2≥(EX)2中出现所需要的式子x2+y2和x+y之间的关系.故此法带有很强的灵活性和技巧性，必须熟练掌握才能运用自如.

方法八：极坐标法

由极坐标，得x2+y2=ρ2,x=ρcosθ，y=ρsinθ(ρ>0)，则

(ρcosθ-1)2+(ρsinθ-1)2=1

化简，得2ρ(sinθ+cosθ)=ρ2+1.

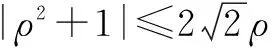
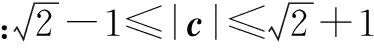
评注 利用平面直角坐标(x,y)与极坐标(ρ,θ)之间的相互转化公式x2+y2=ρ2、x=ρcosθ、y=ρsinθ(ρ>0,θ∈R)，可把原问题转化为极坐标问题进行求解，这样使解题思路直观明朗，容易掌握.

G632

B

1008-0333(2016)22-0025-02