基于张量分解的MIMO多中继系统半盲信道估计方法

穆晓敏， 刘 越， 李双志， 张建康

(郑州大学 信息工程学院，河南 郑州450001)



基于张量分解的MIMO多中继系统半盲信道估计方法

穆晓敏， 刘 越， 李双志， 张建康

(郑州大学 信息工程学院，河南 郑州450001)

针对多输入多输出三跳中继系统，提出了一种基于张量分解的半盲信道估计方法.该方法通过对接收信号构造基于张量分解的PARAFAC和PARATUCK2模型，通过两阶段的迭代算法拟合张量模型.两阶段迭代算法利用ALS拟合PARAFAC模型估计复合信道和发送信号，并利用TALS拟合PARATUCK2模型并行估计三跳信道矩阵.与已有的信道估计方法相比，该方法只需少量的导频序列便能并行估计三跳信道矩阵，不仅可以避免误差叠加，而且提高了系统的频谱利用率，仿真结果验证了其有效性.

MIMO多中继系统；半盲信道估计；张量分解；两阶段迭代算法

0 引言

多输入多输出(Multiple Input Multiple Output，MIMO)中继通信能扩展无线网络的覆盖面积，提高整个通信链路的有效性和可靠性[1-2]，因此MIMO中继技术在无线通信领域得到了广泛关注.当MIMO中继系统的中继节点的处理能力有限时，放大转发(Amplify and Forward，AF)策略由于实现简单而被广泛应用.MIMO中继系统的编码设计、系统链路的可靠性等都依赖于各个链路的信道状态信息(Channel State Information，CSI)的准确度.因此，精确的信道估计技术在MIMO中继系统信中具有非常重要的意义.

在两跳MIMO中继系统中，可以用基于导频的最小二乘(Least Square，LS)方法估计信道矩阵.然而在多跳中继系统中，LS估计方法虽能估计CSI，但存在误差累积[3-4]，并且当接收端天线数小于发送端天线数时无法有效估计信道矩阵.近年来，张量分解被广泛应用于信号处理和信道估计领域[5-9]，文献[6-9]探究了基于平行因子分析(Parallel Factor Analysis，PARAFAC)的信道估计方法，与基于导频的LS信道估计方法相比，这种方法避免了误差叠加.然而针对三跳的MIMO系统，基于PARAFAC方法不能同时分离三跳的信道矩阵.文献[3-9]只考虑两跳中继，为了增加网络的覆盖面积以及抵制深度衰落，有必要引入多跳MIMO中继系统，但上述文献的方法并不全适用于多跳的MIMO中继系统.

针对三跳MIMO中继系统，文献[10]的方法需要在信源多次发送导频序列，降低了整个系统的频谱利用率；笔者提出了基于张量分解的MIMO中继系统半盲信道估计方法,所提算法对接收信号建立PARAFAC和PARATUCK2分解模型，利用两个阶段的迭代算法.第一阶段用交替最小二乘(ALS)拟合PARAFAC模型，联合估计复合信道和发送信号；第二阶段用三线性交替最小二乘(TALS)拟合PARATUCK2模型，同时估计三跳信道矩阵.与文献[10]相比，笔者所提算法只需少量的导频便可同时估计各个链路的信道矩阵，提高了系统的频谱利用率.

1 系统与信号模型

1.1 系统模型

考虑三跳MIMO AF中继系统，如图1所示，信源发送的信息经过第一层中继放大转发到第二层中继，再由第二层中继放大转发到信宿.信源、第一层中继、第二层中继和信宿分别配置MS、M1、M2和MD根天线.信源到中继R1、中继R1到R2、中继R2到信宿的信道矩阵分别为Hsr∈M1×MS、Hrr∈M2×M1、Hrd∈MD×M2.假设系统信道矩阵和噪声矩阵均服从均值为0，方差为1的独立同分布复高斯变量.但由于长距离的路径损耗，不考虑直连链路.

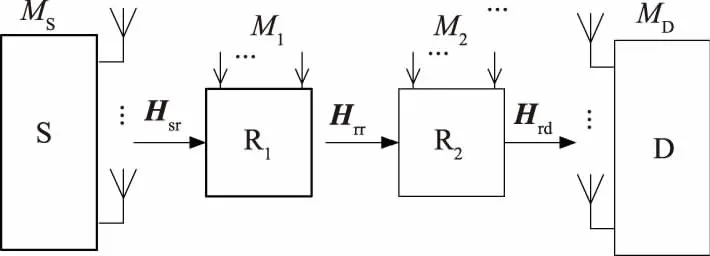
图1 三跳MIMO AF中继系统框图

信源和信宿的通信过程分为三个阶段，第一个阶段信源发送信号矢量s(t)∈MS×1到中继R1；第二个阶段中继R1放大转发第一阶段接收的信号到中继R2；在第三阶段中继R2放大转发第二阶段接收的信号到信宿，信宿接收的信号为

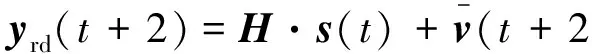
(1)

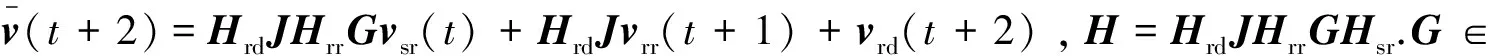
1.2 信号模型

考虑KRST(Khatri-Rao space-time)编码[11]，信源分N个符号块发送信号，假设在整个观测时间信道状态信息是静态不变的，根据式(1)和KRST的编码规则，在n(n=1,2,3,…,N)个符号块、第t(t=1,2,3,…,T)个时隙目的节点接收到的信号为

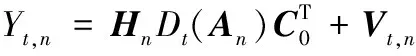
(2)

式中，An=(ΘSn)T∈T×MS.其中Sn∈MS×T表示在第n个符号块的信号矩阵；Θ∈MS×MS为星座旋转矩阵[11]；C0为范德蒙生成矩阵[11]；Dt(An)表示用矩阵An的第t行作为生成矩阵的主对角元素，其他元素为0；Hn=HrdJnHrrGnHsr表示在第n个符号块的复合信通矩阵；Gn∈M1×M1和Jn∈M2×M2分别表示在n个符号块和第t个时隙R1和R2的放大矩阵.

2 张量建模及其唯一性分析

2.1 PARAFAC模型及其唯一性分析

把式(2)中T个矩阵沿着t(第三维)方向堆叠，可以形成一组三维的张量信号Hn∈MD×K×T，通过分析接收信号可表达为

an(t,mS)+vn(mD,k,t).

(3)

其中，hn(mD,mS)表示矩阵Hn中第mD行的第mS列元素.根据参考文献[6-8]，PARAFAC的分解唯一必须满足以下条件：

(4)

由式(4)可以看出，通过调整MS、T和MD均可使不等式成立.因此，要满足唯一性条件，可在发送信号的时隙数与收发天线数之间进行折中.

2.2PARATUCK2模型及其唯一性分析

基于PARAFAC模型可以估计复合信道矩阵Hn，然后基于PARATUCK2模型可以并行估计各链路的信道矩阵.定义复合信道为

Hn=HrdDn(F)HrrDn(E)Hsr.

(5)其中，Dn(F)=Jn，Dn(E)=Gn.矩阵E∈N×M1和F∈N×M2的第n行元素分别包含第n个符号块的两个中继的放大因子.

等式(5)符合张量的PARATUCK2分解模型[5，10]，把式(5)中N个复合信道堆叠到一起，可以形成一组三维张量H∈MD×MS×N.为了同时估计三跳信道矩阵，需对三维张量H∈MD×MS×N进行展开和矢量化操作.根据PARATUCK2模型[10]的3种展开形式，式(5)的3种展开形式为

vec(H(1))=W1vec(Hrr) .

(6)

H(2)=(IN⊗Hrd)W2Hsr.

(7)

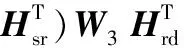
(8)

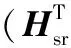
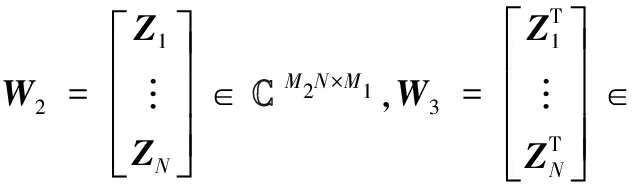
MDMSN≥M1M2,MDN≥M1,MSN≥M2.

(9)

对于传统三阶段LS信道估计方法[10]，各节点的天线数要求MD≥M2≥M1，而本文所提算法在各节点天线数的设置(参见式(9))宽松了接收端对天线数的限制.

3 两阶段迭代拟合算法

算法分两个阶段，首先用ALS迭代算法拟合PARAFAC模型估计复合信道矩阵Hn；其次用TALS迭代算法拟合PARATUCK2模型同时估计三跳信道矩阵.基于PARAFAC模型[12]的两种展开形式为

Yn,MD×KT=Hn(An⊙C0)T+Vn,(1).

(10)

Yn,T×MDK=An(C0⊙Hn)T+Vn,(2).

(11)

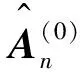
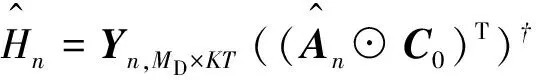
(12)

式中：(·)†表示矩阵的伪逆运算.

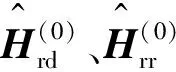
(13)

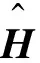
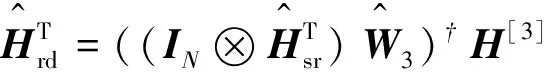
(14)

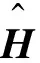
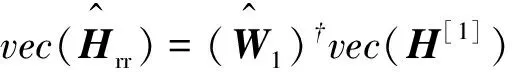
(15)

第一阶段(ALS算法):

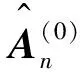
(2)i←i+1.

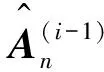
第二阶段(TALS算法)：

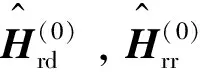
(6)i←i+1.

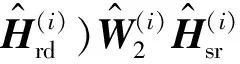
4 仿真与分析

仿真的基本参数设置为:ε=10-6；信源的发射功率为PS，中继的发射功率Pr1=Pr2=30dB.假定系统噪声和信道矩阵均服从均值为0方差为1的独立同分布复高斯随机变量.中继的放大矩阵在接收端已知，E和F选择服从[-1，1]均匀分布的随机序列，目的是使中继的放大因子在每个符号块中都有随机相位[10].编码方式考虑KRST编码[11]，KRST编码可以使系统获得大的分集增益和编码增益，信源发送的信号由正交相移键控QPSK调制生成.所提算法的性能由归一化均方误差(NMSE)衡量，假设Hc=HrdHrr·Hsr为级联信道矩阵，NMSE可以定义如式(16)所示，其中M为蒙特卡洛仿真次数.信道矩阵Hrd，Hrr和Hsr的NMSE定义与式(16)类似.

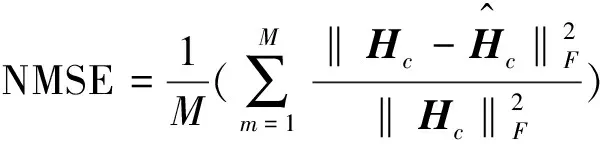
图2比较了笔者所提算法和传统算法及文献[10]所提算法的NMSE性能，其中基于导频的LS估计算法信道矩阵Hrr和Hrd的NMSE不随PS的变化而变化.因此，图中只显示了传统LS方法Hsr的NMSE.由仿真结果可知，所提算法与文献[10]相比性能接近.但是文献[10]基于PARATUCK2分解的信道估计方法需要信源发送大量的导频序列，而本文笔者所提算法只需少量的导频序列，既节省导频的开销，又提高了整个系统的频谱利用率.

图3考察了发送符号块数(N)对系统性能的影响.由仿真结果可知,随着N的增加系统NMSE估计性能提高,这是因为由式(6)～(8)和式(16)分别计算信道矩阵和系统的归一化均方误差，均与N有关.其物理意义为：当N增加时，所构造的PARATUCK2模型中的信道相关信息增多，数据观测时间长，因此提高了系统估计精度.然而当N增加时,三阶张量的维数增加，式(6)～(8)展开后矩阵的维数却随着N的增大而增大，因此这种估计精度的提高是以高的计算复杂度为代价的.

图2 不同符号功率下的信道归一化均方误差

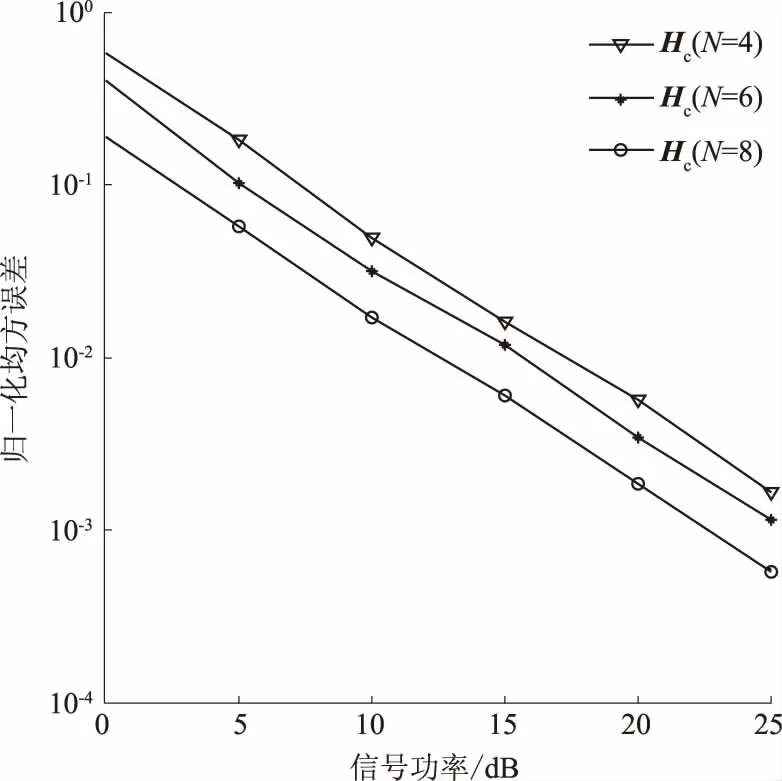
图3 不同符号功率下信道归一化均方误差

5 结论

针对三跳MIMO AF中继系统的信道估计问题，基于张量的PARAFAC和PARATUCK2分解提出了一种半盲信道估计方法.该方法能联合估计各链路的信道矩阵和发送信号，与传统的基于导频的LS信道估计方法相比，首先本文所提算法不存在误差叠加，其次宽松了接收端对天线数的限制，并且在发射端只需少量的导频序列就能并行估计各个链路的信道状态信息，提高了系统的频谱利用率.除此之外，寻找新的迭代拟合算法将是下一步工作的重点.

[1] MO R H, CHEW Y H, YUEN C. Information rate

and relay precoder design for amplify-and-forward MIMO relay networks with imperfect channel state information [J]. IEEE Trans Vehicular, 2012, 61(9): 3958-3968.

[2] RONG Y. Optimal joint source and relay beam forming for MIMO relays with direct link [J]. IEEE Commun Lett, 2010, 14(5): 390-392.

[3] KONG T, HUA Y B. Optimal channel estimation and training design for MIMO relays[C]//Pacific Grove, CA, IEEE Signals, Systems and Computers, Asilomar,USA:IEEE press 2010: 663-667.

[4] KONG T, HUA Y B. Optimal design of source and relay pilots for MIMO relay channel estimation [J]. IEEE Tran on Signal Process, 2011, 59(9): 4438-4446.

[5] XIMENES L R, FAVIER G. PARAFAC-P semi-blind receivers for two-hop cooperative MIMO relay systems [J]. IEEE Trans on Signal Process, 2014, 62(14): 3604-3615.

[6] RONG Y, KHANDAKER M R A, XIANG Y. Channel estimation of dual-hop MIMO relay system via parallel factor analysis [J]. IEEE Trans on Wireless Comm, 2012, 11(6): 2224-2233.

[7] DU J H, YUAN C W, ZHANG J B. Low complexity PARAFAC-based channel estimation for non-regenerative MIMO relay systems [J]. IET Commun, 2014, 8(12): 2193-2199.

[8] FERNANDES C A R, DE ALMEIDA A L F, DA COSTA D B. Unied tensor modeling for blind receivers in multiuser uplink cooperative systems [J]. IEEE Signal Process Lett, 2012, 19(5): 247-250.

[9] DE ALMEIDA A L F, FERNANDES C A R, DA COSTA D B. Multiuser detection for uplink DS-CDMA amplify and forward relaying systems [J]. IEEE Signal Process Lett, 2013, 20(7): 697-700.

[10]HAN X, DE ALMEIDA A L F, YANG Z. Channel estimation for MIMO multirelay systems using a tensor approach [J]. Eurasip J Adv Sign Process， 2014(1): 1-14.

[11]SIDIROPOULOS N D, BUDAMPATI R S. Khatri-Rao space-time codes [J]. IEEE Trans on Signal Process, 2002, 50(10): 2396-2407.

[12]张贤达.矩阵分析与应用[M].北京:清华大学出版社, 2013： 596-600.Tensor-Based Semi-Blind Channel Estimation Method for Three-Hop MIMO Relay Systems

MU Xiaomin, LIU Yue, LI Shuangzhi, ZHANG Jiankang

(School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China)

A novel semi-blind channel estimation was devised to jointly estimate the channel matrices of all links in a three-hop multiple-input multiple-output relay system. A PARAFAC and a PARATUCK2 tensor model of the received signal were constructed, and the proposed algorithm used a two-stage iterative fitting algorithm for tensor model. The ALS algorithm was used to fit the PARAFAC tensor model in the process of estimating the compound channel matrix. Then the TALS algorithm was used to fit the PARATUCK2 tensor model in the process of extracting all the sub-channel matrices. The proposed algorithm could loose the limitation on the number of antennas at the destination node. Moreover, compared with existing methods, the proposed algorithm could avoid error propagation as well as improve the spectral efficiency with few pilots. Numerical examples demonstrated the effectiveness of the proposed algorithm.

MIMO multi-relay system; Semi-blind channel estimation; tensor decom position;two-stage iterative algorithm

2015-11-28；

2016-01-12

国家自然科学基金资助项目(61271421)；国家自然科学基金青年科学基金资助项目(61301150)

穆晓敏(1955—)，女，河南郑州人，郑州大学教授，博士生导师，主要从事多天线无线通信系统、信号处理等研究，E-mail: iexmmu@zzu.edu.cn.

1671-6833(2016)06-0083-04

TN92

A

10.13705/j.issn.1671-6833.2016.03.030