基于变密度法的清扫车举升油缸支架结构设计与分析
邓亚东,张 坤,金德先
(1.武汉理工大学 汽车工程学院,湖北 武汉430070; 2.现代汽车零部件技术湖北省重点实验室,湖北 武汉430070; 3.武汉优力汽车技术发展有限公司,湖北 武汉430070)
基于变密度法的清扫车举升油缸支架结构设计与分析
邓亚东1,2,张 坤1,2,金德先3
(1.武汉理工大学 汽车工程学院,湖北 武汉430070; 2.现代汽车零部件技术湖北省重点实验室,湖北 武汉430070; 3.武汉优力汽车技术发展有限公司,湖北 武汉430070)
为了得到简单可靠的清扫车举升油缸支架结构,建立了以体积分数(Volume Fraction)为约束条件、以结构加权应变能(Weighted Compliance)为目标函数的变密度法(Variable Density Method)拓扑优化数学模型,利用线性近似的方法,分析了采用复合式垃圾箱的道路清扫车在倾倒垃圾过程中油缸支架的受力状况,确定了举升起始工况和检修工况作为设计油缸支架的主要受力工况.采用变密度法对油缸支架进行了拓扑优化设计.在考虑制造工艺可靠性的前提下,以拓扑优化结果为基础建立了清扫车举升油缸支架的三维模型,并进行了线性静态分析.结果表明,基于变密度法设计的清扫车举升油缸支架结构简单,占用空间小,最大应力与最大应变均处于合理范围,满足使用要求.
清扫车;油缸支架;变密度法;加权应变能;拓扑优化
0 引言
道路清扫车作为一种自动收集地面垃圾及尘土的环卫机械,受到各地环卫部门越来越高的重视.高压冲洗、自动避障等功能逐渐成为道路清扫车的标准配置.8 t、16 t等大中型道路清扫车单次清扫面积大、效率高,已成为各城市的主力清扫车辆.市场的巨大需求令国内市场涌现出了许多环卫机械生产企业.与国外相比,我国清扫车水平仍有一定差距,主要表现在以下几点:一是缺乏核心技术,高压水泵等零部件基本依赖进口,风机体积大,功率低;二是整车集成能力不足,倾向保守设计,导致清扫车整备质量大,有效载荷低[1-3].在现有条件的基础上,优化清扫车各系统零部件结构,对于提高产品质量非常重要.安息角的存在使清扫车需要举升一定的角度,才能使垃圾箱内的垃圾完全自动倒出.由于污水占据了垃圾箱内垃圾的绝大部分,为保证垃圾箱能够平稳举升,清扫车一般采用双举升油缸设计方案.举升油缸上端铰接在垃圾箱底部,下端通过油缸支架连接于副车架上.在举升垃圾箱倾倒垃圾的过程中,垃圾箱内的垃圾残留量及其位置是无法确定的,与垃圾的成分(如泥沙与树叶的百分比等)、垃圾与垃圾箱底板的摩擦系数有关,因此油缸支架承受到的力也无法准确获得.对于风机中置的清扫车来说,举升油缸支架与风机前后还需要布置电动隔膜泵、水路控制刀阀、PCL控制器、吸嘴上吸管、高低压水路、液压油路等各种零部件,留给垃圾箱举升油缸支架的空间十分有限[4-5].在复杂的空间限制下,结合举升油缸支架的受力情况,对举升油缸支架进行合理设计十分必要.
1 基于变密度法的结构拓扑优化方法
结构拓扑优化设计有三个要素:设计变量、目标函数和约束条件.解决结构拓扑优化设计问题的过程就是一个在满足约束条件的要求下寻求使目标函数达到理想值的设计变量的过程[6].基于变密度法的结构拓扑优化设计中,其基本思想是采用有限元方法对结构进行离散,并假设材料的弹性模量与材料的密度为确定的数学关系,且每个单元的密度为一个优化设计变量,其大小在区间[0,1]变化.常用的插值函数模型有固体各向同性惩罚微结构模型(Solid Isotropic Material with Penalization,SIMP)和材料属性的合理近似模型(Rational Approximation of Material Properties,RAMP).SIMP密度函数插值模型的数学形式如下:
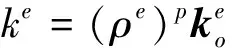
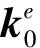
当优化后的单元密度接近0时,表示该单元弹性模量接近0,即该单元对考察的优化工况没有贡献,应被剔除,宏观上表现为一个没有材料分布的小孔;若单元密度接近1,表示该单元的贡献量大,该单元需要优先保留,宏观上表现为承受载荷的实体.优化的约束条件可以是结构的质量、体积、质量分数、体积分数和频度等;目标函数可以是结构的加权应变能最小、最大应力或最大应变不超过给定值等.以体积分数为约束条件、以结构加权应变能为目标函数的变密度法拓扑优化设计数学模型可简写为[7]
(2)
式中:U为结构加权应变能;N为单元总数;M为工况总数;i为工况编号,i=1,2,…,M;Wi为第i个工况的加权系数;ue为第e个单元节点位移向量;Ω为结构的全体设计空间;ρedΩ表示第e个单元的体积;∫ΩρedΩ表示优化后的结构体积;V0为全体设计空间的初始体积;ε为体积分数;
式(2)中的第3个方程即表示体积分数约束条件;F为结构力向量;k为结构总刚度矩阵;u为结构位移向量;式(2)中其他参数的含义与式(1)相同.
解决此优化问题的步骤如下所示:
a)离散设计区域,建立有限元模型;
b)确定目标函数和约束条件,定义单元设计变量并初始化;
c)对有限元模型进行结构分析,计算各单元刚度矩阵与结点位移;
d)计算总体结构的应变能及其灵敏度,求解拉格朗日乘子;
e)利用优化准则法(OptimizationCriteria,OC)对设计变量进行迭代计算;
f)检查约束条件是否满足,若不满足则返回上一步;
g)对每一步迭代产生的结果进行收敛性检查.若将目标函数加权应变能作为迭代控制量,则收敛性评判标准为式(2).若将设计变量定义为迭代控制量,则收敛性评判标准为式(3).
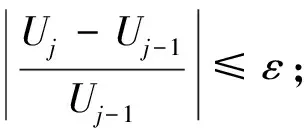
(3)
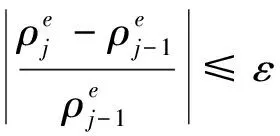
(4)
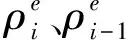
h) 若上一步迭代结果收敛,则可得到结构的最优拓扑形式.若不收敛,则返回至第c)步继续迭代,直至结果收敛[8].
2 清扫车举升油缸工况分析
图1是与该清扫车举升油缸相关的零部件装配图,复合式垃圾箱处于举升状态.复合式垃圾箱由前部清水箱和后部垃圾箱组成,二者焊接为一体.油缸支架的两端分别通过螺栓固定在副车架的横梁上,中部开圆孔.举升油缸外侧吊耳穿过油缸支架中部的圆孔,传递沿油缸轴线方向的力,每两个油缸支架共同支承一个举升油缸.
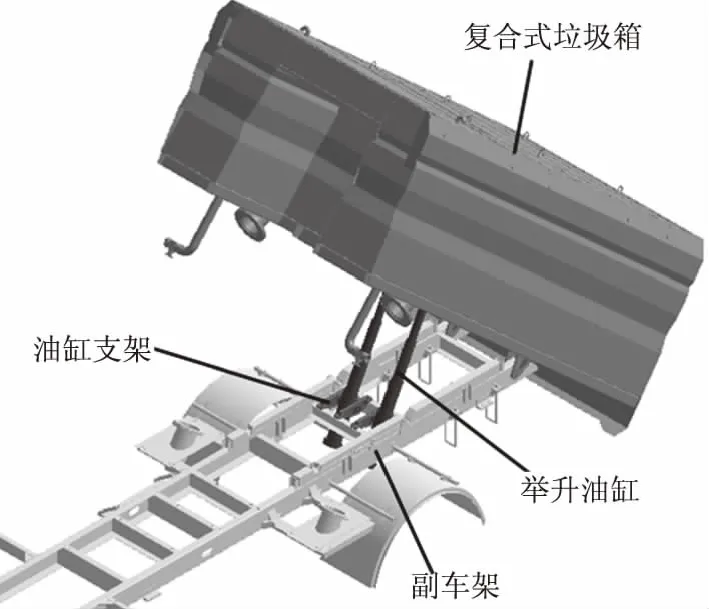
图1 处于举升状态的复合式垃圾箱
清扫车执行清扫作业时,垃圾箱依靠自身重力固定在副车架上,清水箱的存水量由多变少,垃圾箱里的垃圾逐渐增加.此时清扫车举升油缸处于非工作状态,油缸支架基本不受力.
清扫车倾倒垃圾时,清水箱无水,垃圾箱处于满载垃圾状态,三级举升油缸缓慢举升复合式垃圾箱,垃圾箱门同时打开,垃圾自动倒出.倾倒作业完成后,液压油泵关闭,复合式垃圾箱在自身重力下缓慢下落,并最终压紧在副车架上.举升油缸施加给复合式垃圾箱的力随着垃圾箱中垃圾残留量及垃圾箱举升角度而变化.
在清扫车纵向中心平面内,以复合式垃圾箱与副车架的铰接点为坐标原点O,清扫车前进方向为X轴正向,竖直向上为Y轴正向,建立如图2所示的直角坐标系XOY.
记:G1为空载的复合式垃圾箱重量;(X1,Y1)为空载的复合式垃圾箱质心坐标;F0为举升油缸沿其轴线方向的力大小;θ为F0与Y轴正向之间的夹角;(X0,Y0)为油缸上支点坐标;G2为残留垃圾的总重量;(X2,Y2)为残留垃圾质心坐标;(X3,Y3)为油缸下支点坐标.
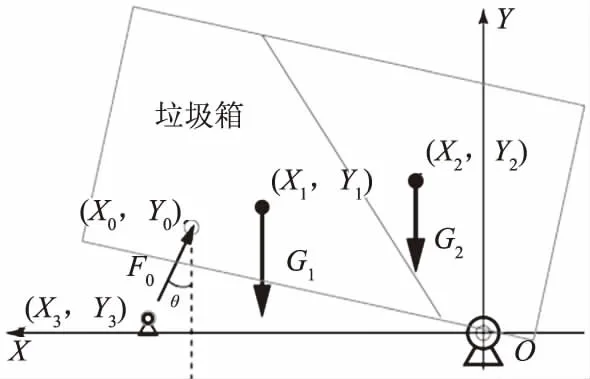
图2 复合式垃圾箱受力简图
根据设计要求,θ在垃圾箱举升过程中由9.21°增加至27.61°.以举升过程中的复合式垃圾箱及其内部垃圾为研究对象.由于举升过程十分缓慢,可假设在举升过程中,研究对象处于静力平衡状态,对其在O点取力矩平衡方程,有
F0X0cosθ+F0Y0sinθ-G1X1-G2X2=0.
(5)
则可求得
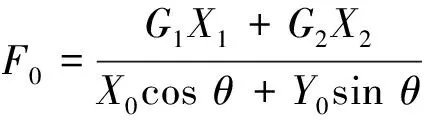
(6)
根据牛顿第三定律易知,举升油缸作用于油缸支架上的力大小也为F0.由于油缸支架宽度较小,忽略沿支架支撑孔轴线方向上力的变化,则单个油缸支架的受力大小为
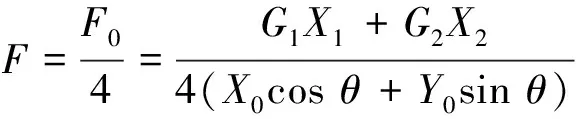
(7)
F与Y轴负方向的夹角为θ.式(7)中,G1为常数,X1、X0、Y0均可由道路清扫车几何关系表示为θ的函数.关键的问题在于举升过程中,垃圾箱内的垃圾残留量及其位置是无法确定的,与垃圾的成分(如泥沙与树叶的百分比等)、垃圾与垃圾箱底板的摩擦系数有关.
假设在举升过程中,垃圾残留量与其质心位置随着θ线性变化.举升开始时,垃圾残留量为清扫车垃圾箱最大有效容积V2=4.36m3.假设垃圾在垃圾箱内是均匀分布的,其密度为ρ=1.5×103kg/m3.取重力加速度g=9.8N/kg,则举升初始状态下的垃圾残留量G2为
G2=V2ρg=4.36×1.5×103×
9.8(N)=64 092(N).
(8)
X2的初始值可由相应的三维建模软件求得.举升初始状态下的X2=905.50mm.
举升结束时,垃圾箱内的垃圾倾倒完毕,G2和X2均为零.由于假设G2和X2随θ线性变化,易得
G2=-355.40θ+9 812.49;
(9)
X2=-49.21θ+1 358.59.
(10)
式中:θ单位为度(°);G2单位为N;X2单位为mm.
由式(7)、(9)、(10)及X1、X0、Y0与θ的几何关系,可求得F与θ的关系,计算结果如表1所示.

表1 举升过程中油缸支架受力特性
清扫车在检修过程中,往往需要举升垃圾箱至最大举升角度.此时垃圾箱中没有垃圾和清水,车辆处于空载状态.此时垃圾箱的工况与举升工况下θ=27.61°时的状态一致,油缸支架的受力状态也一致.
取θ=9.21°时的举升起始工况和θ=27.61°的检修工况作为计算油缸支架的主要受力工况.
3 油缸支架拓扑优化设计
设计空间是设计变量的集合,指在拓扑优化设计中需要优化改变其形状的区域[9].非设计空间指在拓扑优化中形状保持不变的区域.油缸支架依靠4个M14的螺栓固定在副车架的横梁上(图3中A区域).油缸中部的圆孔与举升油缸外侧的吊耳相连(图3中B区域).这两个部分是需要保持不变的.为了尽可能给支架附近的其它零部件保留足够大的布置空间,支架中间部分的厚度小于该零件最大宽度.
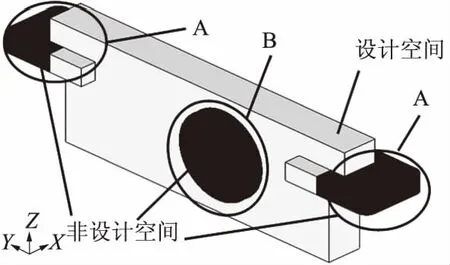
图3 油缸支架拓扑优化的设计空间(灰色)与非设计空间(黑色)
为保证油缸支架在工作过程中的应力和变形处于一定的范围内,定义目标函数为结构的加权应变能(weighted compliance)最小.约束条件定义为结构设计空间的体积分数(volume fraction),其上限设置为0.3.定义两种工况具有相等的加权系数0.5[10].油缸支架采用球墨铸铁QT500-7铸造而成,其物理特性如表2所示.

表2 QT500-7物理特性
油缸支架左右对称.为避免蜂窝状结构的出现,定义零件向两侧拔模,最小尺寸设为A部分的厚度.
经过25次迭代后,拓扑优化设计结果收敛.将密度xi阀值设置为0.3,密度大于阀值的单元都需要保留,得到举升油缸支架的拓扑优化结果,如图4所示.
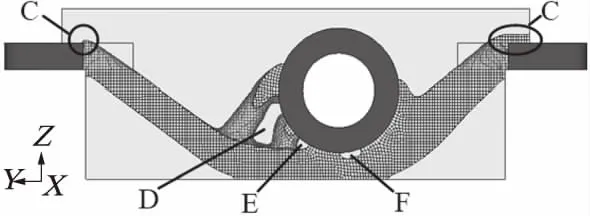
图4 密度大于0.3的拓扑优化区域
4 油缸支架的建模、分析与应用
考虑到制造工艺的可行性,拓扑优化的结果并不能直接作为设计方案,需要经过一定的修改.
注意到图4所示的C区域,设计空间的高度稍微超出了螺栓孔部分的厚度.为避免出现应力集中现象,并考虑螺栓安装的方便性,将螺栓孔部分的厚度增大至与其相连的设计空间厚度.
左侧通孔D用一个长孔替代.中间通孔E与右侧通孔F由于孔径过小,忽略不计.A区域与设计空间的两侧采用圆滑过渡连接.油缸支架设计方案如图5所示,单件质量5.7 kg.
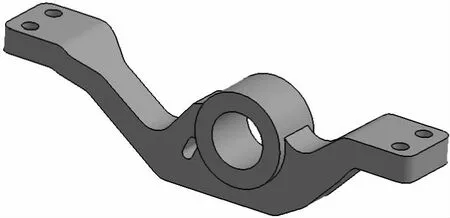
图5 油缸支架设计方案
对油缸支架进行线性静态分析,分别计算举升起始工况和检修工况下油缸支架的应力分布与变形情况.油缸支架有限元模型采用一阶四面体网格划分,全局网格尺寸2 mm,共有节点52 250个,实体单元234 036个.有限元分析结果如图6至图9所示.
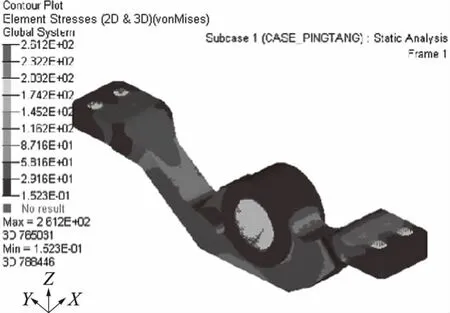
图6 举升起始工况下的油缸支架应力云图
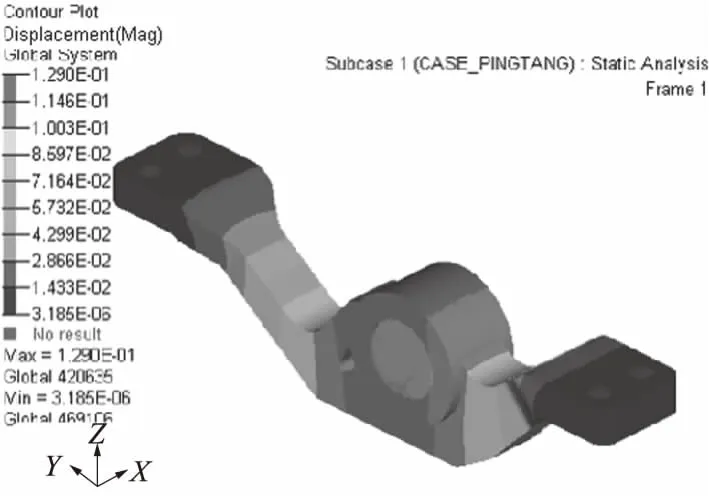
图7 举升起始工况下的油缸支架应变云图
从应力云图上看,两种工况下的应力分布都比较均匀,最大应力出现在举升起始工况下A区域与油缸支架相连接的部分,应力值为261.2 MPa,小于材料屈服强度320 MPa,安全系数为1.23,满足使用要求[3].从应变云图上看,越靠近支架中间区域,应变越大,最大应变出现在举升起始工况下支架通孔D附近,最大应变值为0.129 mm,满足使用要求.检修工况的最大应力为27.9 MPa,最大应变为0.016 mm,远小于举升起始工况.
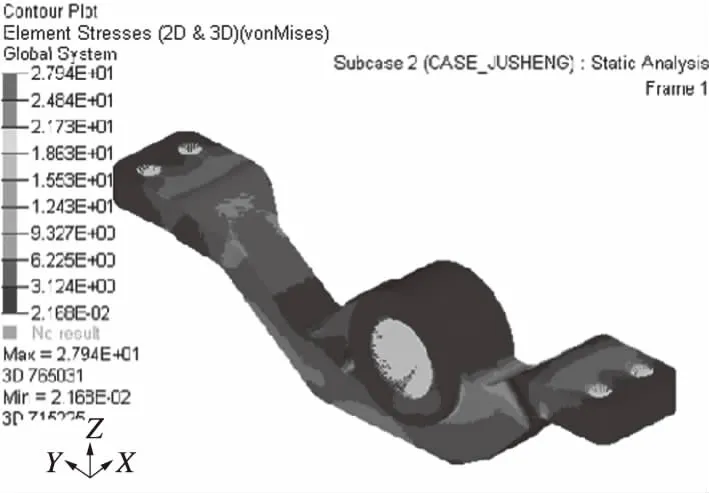
图8 检修工况下的油缸支架应力云图
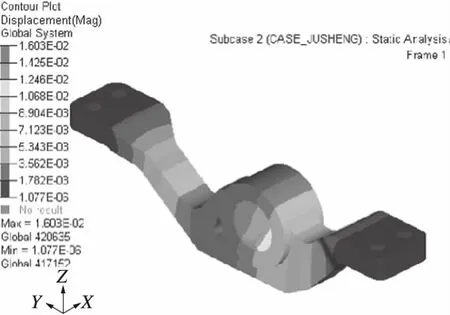
图9 检修工况下的油缸支架应变云图
采用该设计方案的道路清扫车由湖北随州某专用车厂家生产制造,面向全国销售,目前各地区均未出现与油缸支架相关的质量问题.图10所示为清扫车在车间总装和现场调试时的状态.

图10 清扫车的组装与调试
5 结论
(1)虽然在清扫车倾倒垃圾的过程中,复合式垃圾箱内的垃圾残留量与多种因素有关,但是利用线性近似的方法仍然可以近似计算举升油缸及其支架的受力状况.计算结果表明,油缸支架主要有举升起始工况和检修工况两种主要受力状态,且举升起始工况和检修工况的受力大小相差约一个数量级.
(2)基于变密度法建立的油缸支架结构拓扑优化数学模型以单元密度为设计变量,其优化结果代表了油缸支架的最佳结构.在此基础上结合制造可靠性设计的油缸支架,其结构简单,应力分布较为均匀,应力处于合理范围内,满足使用要求.
[1] 樊金曦,陈殿领. 国产道路清扫车技术现状分析[J]. 机械制造, 2013(8):46-49.
[2] 葛恒安,祁隽燕. 公路养护的轻骑兵——国内路面清扫车行业发展现状分析[J]. 交通世界, 2005(6):68-70.
[3] 周雷青. 国内清扫车概况及使用维护[J]. 中国市政工程, 2008(3):88-89.
[4] 张晨光. 清扫车工作装置的匹配性能研究[D].西安:长安大学工程机械学院, 2010.
[5] 张铁山,凌和平. 中型道路清扫车的总体设计与研究[J]. 专用汽车, 2005(2):18-20.
[6] 王智文. 汽车轻量化技术发展现状初探[J]. 汽车工艺与材料, 2009(2):1-5.
[7] RIETZ A. Sufficiency of a finite exponent in SIMP (power law) methods[J]. Structural & multidisciplinary optimization, 2001, 21(2):159-163.
[8] 梁醒培,王辉.基于有限元法的结构优化设计—原理与工程应用[M].北京:清华大学出版社,2010.
[9] 王艳萍,黄友钦,吴玖荣,等. 基于多目标等效风荷载的变截面门式刚架抗风优化[J]. 郑州大学学报(工学版),2014,35(6):59-63.
[10]JIANG Zhengyi, HAN Jingtao, LIU Xianghua. OptiStruct application in optimization design of car cabin front suspension bracket[J]. Advanced materials research, 2011, 421:212-216.
Structure Design and Analysis of the Lifting Hydro-Cylinder Bracket of a Road Sweeper Based on the Variable Density Method
DENG Yadong1,2, ZHANG Kun1,2, JIN Dexian3
(1.School of Vehicle Engineering, Wuhan University of Technology, Wuhan 430070, China; 2.Hubei Key Laboratory of Advanced Technology for Automotive Components, Wuhan 430070, China; 3.Wuhan Union Vehicle Technology Development Co., Ltd Wuhan 430070, China)
In order to design a simple and reliable lifting hydro-cylinder bracket structure, the topology optimization mathematical model based on the Variable Density Method was established by the volume fraction as constraint conditions and the weighted compliance as objective function. By means of linear approximation method, analyzed the force condition of the lifting hydro-cylinder bracket of a road sweeper with composite trash bin in the dumping process and determined lifting starting condition and maintenance condition as the main force conditions for the design of the lifting hydro-cylinder bracket. The topology optimization design of the lifting hydro-cylinder bracket was carried out by using the Variable Density Method. Considering the reliability of manufacturing process, a three dimensional model of the lifting hydro-cylinder bracket was established based on the topology optimization results, and the linear static analysis of the model was carried out. The final results showed that the lifting hydro-cylinder bracket designed by the variable density method had the advantages of simple structure, small occupied space, the largest stress and maximum strain in reasonable range and met the requirements of the application.
road sweeper; hydro-cylinder bracket; variable density method; weighted compliance; topology optimization
2016-05-30;
2016-07-19
国家自然科学基金资助项目(51305132);武汉理工大学重大研究计划和交叉学科创新研究项目(WUT142207005)
邓亚东(1958—),男,湖北黄岗人,武汉理工大学教授,博士生导师,主要研究汽车动力学及其控制,汽车及电动车辆系统分析与设计,E-mail:deyadong@sina.com.
1671-6833(2016)06-0028-06
U463.92
A
10.13705/j.issn.1671-6833.2016.06.023

