全矢-ARMA模型在机械振动强度预测研究的应用

韩 捷,吴彦召,陈 磊,郝旺身,张钱龙

(郑州大学 振动工程研究所，河南 郑州450001)



全矢-ARMA模型在机械振动强度预测研究的应用

韩 捷,吴彦召,陈 磊,郝旺身,张钱龙

(郑州大学 振动工程研究所，河南 郑州450001)

单通道预测方法由于获取振动信息不完善，导致预测结果一致性差，从而不能很好地实现故障的预测.通过全矢谱获得的频谱结构具有唯一性的特点，能够很好地弥补单通道的不足，在此基础上，将时序预测方法ARMA模型与全矢谱技术相结合，提出了全矢-ARMA模型，并把该方法应用到机械振动强度预测研究中.实验表明，该方法预测结果与实际较吻合.

全矢谱；ARMA模型；强度预测；信息融合；时序预测方法

0 引言

趋势预测是机械设备预知维修中重要的组成部分，通过预测可以对设备的故障早知道，从而避免重大事故的发生.1927年，Yule提出了时序的AR模型，用于预测Walker在1931年也用AR模型进行了预测.此后，逐步发展了ARMA模型、多维ARMA模型、非平稳时序模型、非线性时序模型等.时序分析另一个突破为谱分析，产生了与传统的Fourier谱不同的现代谱.1967年，Burg在对地震信号的分析与处理中，提出了最大熵谱(MES).1968年，Parzen提出了AR模型谱.1973年，Pisarenko提出了Pisarenko谱，在谐波上面迭加白噪声进行谱分析.1981年，Shore论述了最小交叉谱.笔者采用的预测方法是时间序列预测模型中的ARMA模型，由于时间序列分析方法在金融经济、气象水文、机械振动等众多领域都有应用，相对比较成熟[1-2].之前很多学者通过单通道的数据信息进行预测，效果不是很理想.由于旋转机械转子的涡动特性，在同一截面传感器安装的方位发生变化，就会得到同一转子下不同的振动信息，也就是通过一个传感器无法获得较为全面的转子振动信息，从而使接下来的预测无法进行.

为了解决通过单一传感器不能获得唯一的机械设备振动信息的问题，韩捷教授[3-5]提出了采用同一截面两个互相垂直的探头同步进行测量，再结合同源信息融合技术提出了全矢谱技术.这一技术利用了旋转机械的回转特性，巧妙地将同一截面的两个互相垂直的振动信号进行融合，结果好比一个虚拟探头在不断移动测得该截面最大的振动强度值.通过该技术可以保证在同一截面下的频谱结构不会随着两个互相垂直的传感器沿圆周方向安装方位的不同而变化.全矢谱技术不仅改进了传统分析方法在分析振动信号判断故障时由于信息不完善造成误判的缺陷，而且也做到了与传统的数据处理分析方法相兼容.

综上所述提出了基于全矢-ARMA模型的机械振动强度预测方法，并与单通道的时间序列预测方法加以比较验证.

1 预测模型的全矢数值计算

把转子的涡动看成是各谐波频率下两个方向的组合运动，其涡动轨迹是各谐波频率下的椭圆，并定义这些椭圆的长半轴为振动强度的主振矢，短半轴为振动强度的副振矢，而转子在各谐波频率下的涡动强度即主振矢是对故障判断和识别的基本依据[3-5].

韩捷教授不但提出了全矢谱技术，并且给出了其全新的快速稳健算法，该算法依据FT变换的奇偶共轭推导出，其主振矢即涡动椭圆的长半轴RLK、副振矢即涡动椭圆的短半轴RSK，如公式(1)所示：

(1)

式中：Xpk为正进动圆半径；Xrk为反进动圆半径；{Zk}为{Zn}的Fourier变换；{Zn}是由序列{xn}、{yn}构成的复序列，即{Zn}={xn}+j{yn}，其中{xn}、{yn}分别是x、y方向上采样得到的离散序列.

有了这个快速稳健的算法，就不需要对两个通道的数据分别进行FT变换，而是对两个通道构成的复序列进行一次FT变换，通过公式(1)就可以得到各谐波频率下的主振矢.现在看来是将各谐波频率下的复杂计算简化为复Fourier变换，使计算量成倍减少同时也较稳健，另外也和传统的数据处理分析方法相兼容.如果在测量时由于某些原因导致一个传感器的数据失效，那么该算法依然成立，完全满足在线检测分析要求.

2 ARMA模型分析方法

ARMA模型是分析时间序列比较全面的方法，由自回归模型(AR模型)与滑动平均模型(MA模型)组合而成.根据时间序列模型的特性可知，ARMA模型适合对均值为零的平稳随机序列建模，然而实际的建模对象往往既包含平稳的随机部分，又含有确定的非随机分量.因此，在进行时间序列建模时，首先需要对观测数据序列进行平稳化处理，使非平稳的数据序列转化为均值为零的平稳随机序列[1-2].时间序列的建模过程如图1所示.

ARMA模型有很多参数估计的方法，本文采用概念上简单明了，避开ARMA建模中大量的繁杂计算，建模速度快的长自回归模型计算残差法.该算法有两次建模，先建AR(p)再建ARMA(n,m)，AR(p)参数估计采用了运算速度较快的burg算法；ARMA(n,m)模型参数估计用了方法简单、参数估计无偏、精度高的最小二乘法.模型适用性检验准则使用的是Akaike信息准则的BIC准则.时间序列ARMA(n,m)模型：

(2)

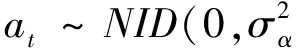
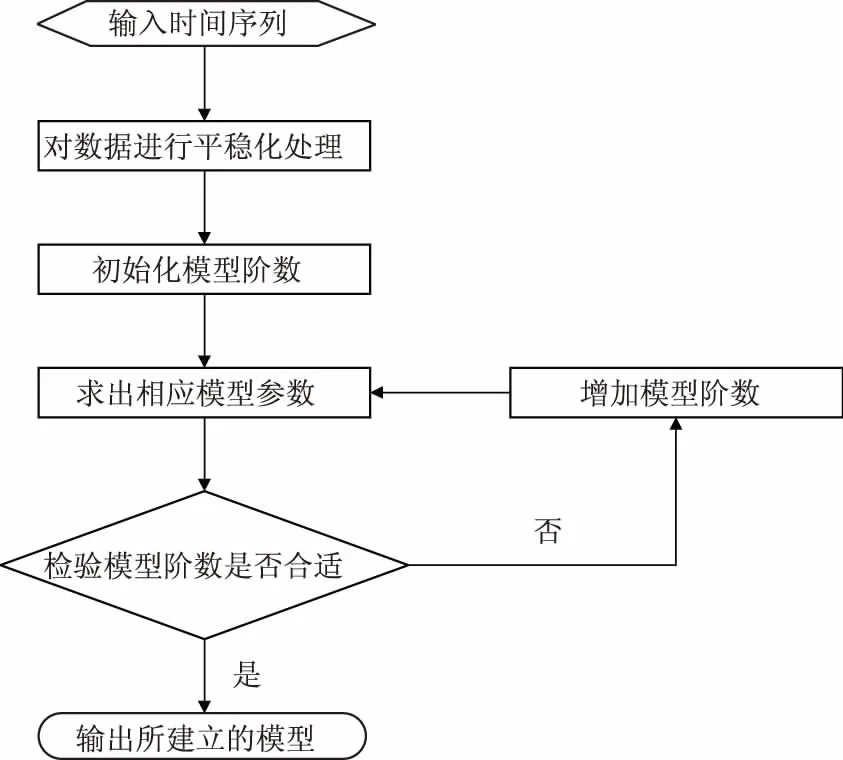
图1 时间序列的建模过程

模型参数估计如下：根据Akaike信息准则确定AR模型阶数p，再由burg算法得到模型参数φi(1,2,…，p)后，由AR(p)模型计算残差序列：

由式(3)可得到从t=p+1至t=N的残差序列{at}，将{at}带入式(2)，可得到如下矩阵方程:

Y=Xβ+A.

式中：

Y=[xp+m+1xp+m+2…xN]T;

A=[ap+m+1ap+m+2…aN]T;

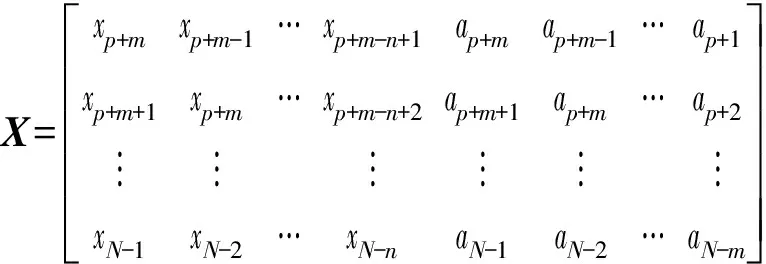
由矩阵方程可知，模型参数β=(XTX)-1XT·Y，矩阵X与Y中xt、at均为已知，可求得模型参数β.由求得的模型参数建立ARMA模型，然后计算由此模型得到的预测值与实际值的误差，根据这些误差求得BIC值.依次修改模型的阶数得到不同的预测模型，求得各个模型的BIC值，然后取较小的BIC值对应的阶数和参数建立合适的ARMA模型.

ARMA(n,m)模型的BIC准则表达式为：

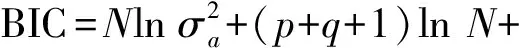
3 全矢-ARMA预测模型的建立[6-11]

基于全矢谱技术和时间序列分析方法建立如下预测模型.

Step1. 假设有N1对等时间间隔的实际数据组成的数组，每对数组存放着两个通道的振动数据，每组数据长度为N2即采样点数，令数组的两个元素分别为{xij}、{yij}(i=0,1,2,…,N1-1;j=0,1,2,…,N2-1).

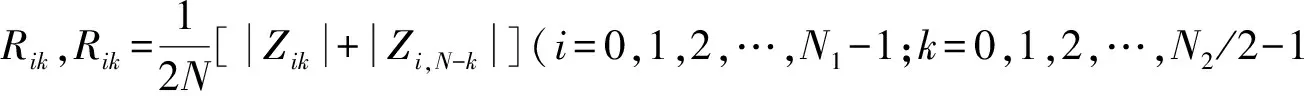
Step3. 针对每个频率k点即{Rik}构造一组时间序列，依据ARMA(n,m)模型建立新的预测模型即全矢-ARMA预测模型：

4 试验研究

在某电厂汽轮机的轴承上采集振动数据，汽轮机的转速为2 990 r/min，工频为49.8 Hz.试验步骤如下：①在泵轴承位置装上两个相互垂直的电涡流位移传感器，调整采样频率为1 600Hz,采样长度为1 024点，进行双通道同步采集，每隔2 h采集一组数据共采集数据60组.②利用全矢谱算法求出每组数据的主振矢频谱，并将其放入数组R[60][400].③从前50个频谱图上得到五倍频以内所有频率点幅值，根据每个频率点下的50个数据建立合适的ARMA模型，利用该模型单步预测第51到56个频谱图.

下面以一倍频的主振矢作为原始数据建立全矢-ARMA模型，其他各个频率点的建模过程和一倍频的建模一样.由图2(a)可以看出，振动信号的特征信号非平稳、非线性、规律性较差，直接对其进行预测模型不好确定，精度不高，因此需对其信号进行平稳化处理以及零化处理，处理后的信号图如图2(b)、(c)所示.

根据AR模型的偏自相关系数截尾性以及MA模型的自相关系数截尾性，由图3可以初步确定,ARMA模型的阶数为n=5与m=2，然后根据BIC准则最终确定ARMA模型的阶数为n=5与m=4.BIC值变化图如图4所示.其他频率点的模型阶数选取原则与其一样.x通道与y通道的波形对比和频谱对比如图5和图6所示.

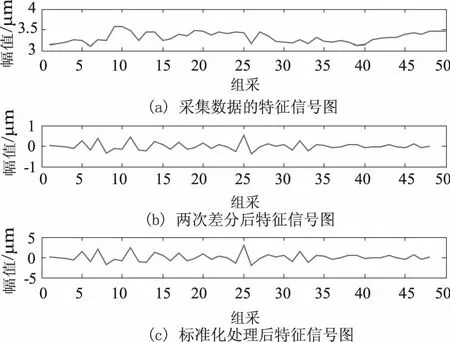
图2 特征信号图以及处理后的信号图

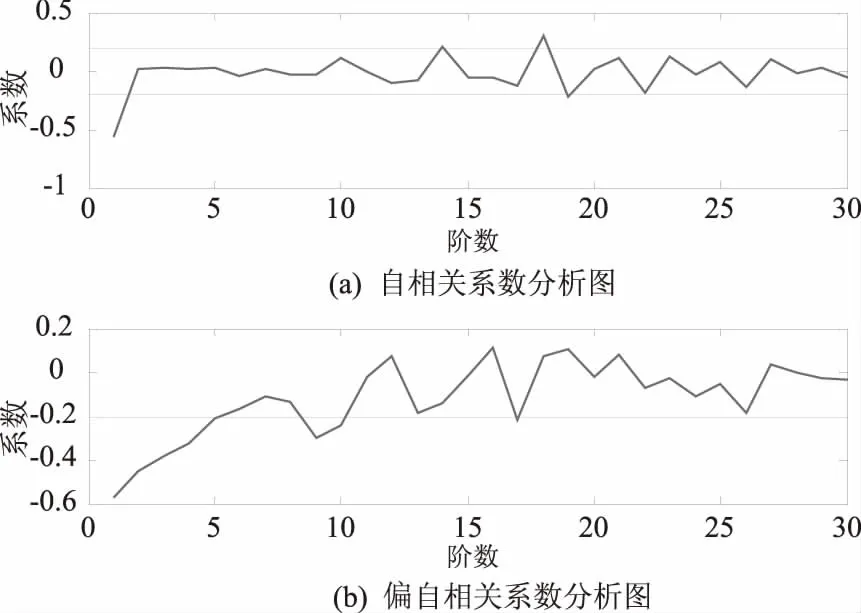
图3 自相关系数与偏自相关系数分析图

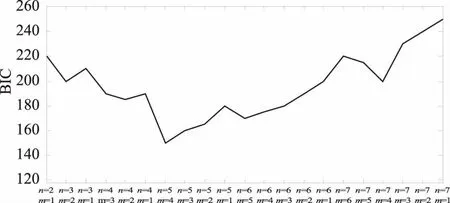
图4 BIC值变化图

由图5和图6可以看出,x通道与y通道的波形图与频谱图存在着明显的差异性，因此x通道与y通道任何一个通道振动信号都不能准确反映转子振动的实际情况，通过单一通道的振动数据进行振动强度的分析是片面的、不准确的.而将两个通道的振动数据通过同源信息融合技术与全矢谱技术进行全矢数值计算得到的全矢谱具有频谱结构唯一性，能够准确反映出转子振动的最大强度.全矢谱图如图7所示.

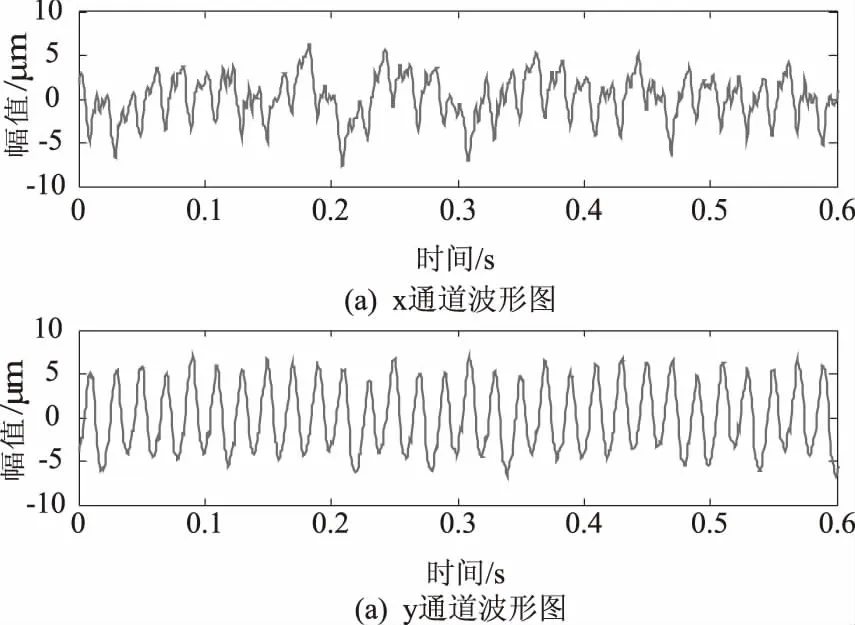
图5 x通道与y通道波形对比图

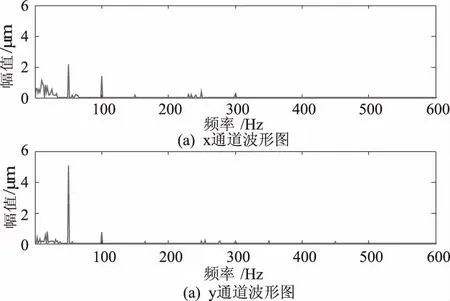
图6 x通道与y通道频谱对比图

图7 振动信号的全矢谱图

第51到56组实际数据的全矢频谱结果以及预测得到的全矢频谱结果如表1所示.不进行全矢数值计算，通过ARMA模型分别对两个单通道进行预测得到的频谱结果如表2和表3所示，然后与全矢-ARMA模型预测的结果(表1)进行对比.

结果表明：通过全矢数值计算得到的频谱结构唯一，并且能够准确反映转子的最大振动强度，因此全矢-ARMA模型能够进行振动强度的预测，得到预测频谱之后可以对设备进行故障的预分析.而两个方向单通道的频谱具有差异性，不能准确反映转子的振动信息，因此不能通过单通道预测进行故障的预分析.

表1 全矢-ARMA模型单步预测误差

表2 x通道单步预测误差

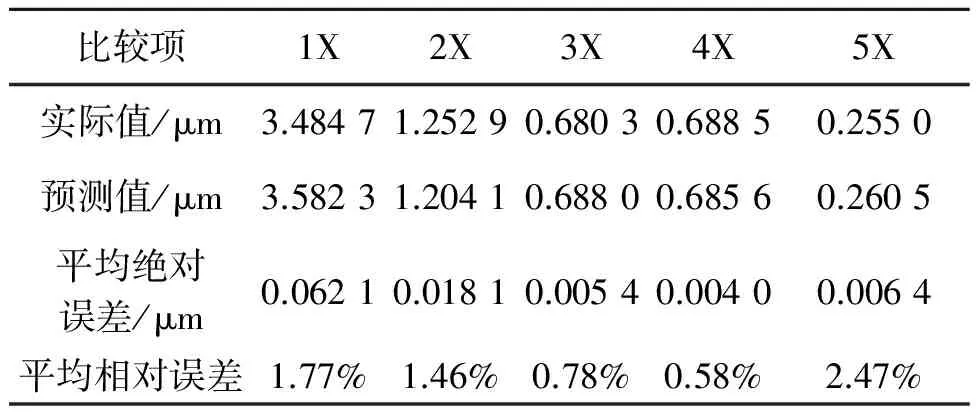
表3 y通道单步预测误差

之前有学者用全矢-AR模型对设备状态趋势进行预测，预测结果平均绝对误差为0.016 1，平均相对误差为2.494 2%[8].倍频预测误差如表1～3所示，由表1数据可以看出，全矢-ARMA模型预测的平均相对误差为0.71%，预测误差小、精度高.由于全矢-ARMA模型在各个频率处都有较高的预测精度，因此预测出的频谱结构也较为准确,有了频谱结构，从而能够实现对故障的预测分析.

通过以上的实验验证可以看出，全矢-ARMA模型预测比单通道预测的结果一致性好，频谱结构预测准确并具有唯一性，有利于故障预测技术的应用.

5 结论

(1)全矢-ARMA模型预测解决了单通道预测信息不完善，频谱结构不唯一的缺陷，实现了频谱结构的预测，并且有较好的预测结果.

(2)全矢-ARMA模型预测能够准确地预测出转子振动的最大强度，因此实现了振动强度的早预测，从而减少重大事故的发生.

(3)根据故障机理由频谱可以知道故障类型，通过全矢-ARMA模型预测的全矢谱图能够实现故障的预分析，从而提前做好维修的准备.

[1] 杨叔子,吴雅,轩建平,等.时间序列分析的工程应用(上册)[M].武汉:华中科技大学出版社,2007.

[2] 易丹辉.时间序列分析方法及应用[M].北京:中国人民大学出版社,2011.

[3] 韩捷,石来德.全矢谱技术及工程应用[M].北京:机械工业出版社,2008.

[4] 韩捷,张瑞林.旋转机械故障机理及诊断技术[M].北京:机械工业出版社,1997.

[5] 韩捷,石来德.旋转机械的全信息能量谱分析方法研究[J].机械强度,2003,25(4):364-368.

[6] 樊碧波,韩捷,张晓冬.基于全矢谱的旋转机械谱强度预测技术研究[J].机械设计与制造,2010(11):217-219.

[7] 韩捷,石来德,董辛旻.旋转机械虚拟探头融合检测技术研究[J].中国工程机械学报,2007,5(2):204-209.

[8] 李永耀,韩捷,陈磊,等.基于AR-Kalman的机械设备状态趋势预测方法研究[J].制造业自动化,2014(12):95-96,120.

[9] AKAIKE H. Maximum likelihood identification of gaussian autoregressive moving average models[J].Biomerica,1973,60(2):102-110.

[10]GOLDMAN P, MUSZYNSKA A. Application of full spect-rum to rotating machinery diagnostics[J].Orbit, 1999(3): 17-21.

[11]BOX G E P, JENKINS G M,REINSEL G C.Time series analysis:forecasting and control[M].SanFrancisco:Wiely,1976.

Application of FVS-ARMA Model in Mechanical Vibration Intensity Prediction Research

HAN Jie, WU Yanzhao, CHEN Lei, HAO Wangshen, ZHANG Qianlong

(Research Institute of Vibration Engineering, Zhengzhou University, Zhengzhou 450001, China)

Considering incomplete vibration information that leading to poor consistency of predictive results, single-channel prediction method cannot realize accurate prediction of machine fault. While by obtaining spectral structure with unique characteristics, full vector spectrum (FVS) can well make up for the deficiency of single-channel. Further the prediction method of FVS-ARMA model was proposed in this paper, which combined ARMA model with full vector spectrum technology. It was applied to predict the mechanical vibration strength. Experiments showed that prediction results of this method were identical to the practical effects.

full vector spectrum; ARMA model; strength prediction; information fusion; time-series forecasting method

2016-06-25；

2016-08-18

国家自然科学基金资助项目(51405453)；河南省教育厅科学技术研究重点项目(13A460673).

韩捷(1958—)，男，河南郑州人，郑州大学教授，博士，博士生导师，研究方向为设备状态监测与智能诊断技术，E-mail:hj_em@163.com.

1671-6833(2016)06-0043-05

TH16;TP277

A

10.13705/j.issn.1671-6833.2016.06.024