压实度和干湿循环对豫东粉土土-水特征曲线的影响

张 涛，乐金朝，张俊然

( 1.郑州大学 水利与环境学院，河南 郑州 450001；2.河南交通职业技术学院 建筑工程系，河南 郑州 451400； 3.华北水利水电大学 河南省岩土力学与结构工程重点实验室，河南 郑州 450045)



压实度和干湿循环对豫东粉土土-水特征曲线的影响

张 涛1,2，乐金朝1，张俊然3

( 1.郑州大学 水利与环境学院，河南 郑州 450001；2.河南交通职业技术学院 建筑工程系，河南 郑州 451400； 3.华北水利水电大学 河南省岩土力学与结构工程重点实验室，河南 郑州 450045)

用GCTS公司土-水特征压力板仪对不同压实度和多次干湿循环后的豫东粉土进行的土-水特征曲线试验.试验结果表明：当吸力小于100 kPa时，土-水特征曲线的脱湿和吸湿曲线具有明显的滞回特性；当吸力大于100 kPa时，滞回特性不明显.土-水特征曲线用含水率和吸力关系表示时，含水率随着压实度和干湿循环次数的增大，脱湿和吸湿曲线均向左下方偏移；土-水特征曲线用饱和度和吸力关系表示时，脱湿和吸湿曲线随着压实度的增加均向右上方偏移，并随着干湿循环次数的增加向左下方偏移.用Matlab中的Lsqcurvefit函数对试验数据进行拟合并得到Van Genuchten模型中的拟合参数.

豫东粉土；土-水特征曲线；压实度；干湿循环；预测

0 引言

传统的公路工程设计大部分都是依据饱和土力学原理，而实际工程中路基土大部分以非饱和状态存在，亟待用非饱和理论对路基土进行深入研究.土-水特征曲线(简称SWCC)是研究非饱和土力学性质的核心[1]，对解决非饱和土公路路基工程问题具有重要的意义.压实度和干湿循环作用对土-水特征曲线的影响，已有很多学者进行了大量的研究.王协群等[2]、张雪东等[3]、汪东林等[4]、叶灵敏等[5]等研究了压实度对不同土体土-水特征曲线的影响；刘奉银等[6]、杨俊等[7]、乐金朝等[8]研究了干湿循环作用的影响.Ng和Pang[9]、Ho[10]研究了多次干湿循环的土-水特征曲线.张俊然等[11]结合已有的数据总结了脱湿曲线和吸湿曲线随着干湿循环次数的变化规律，提出了能预测多次干湿循环后土-水特征曲线的方法.但对河南东部地区粉土(简称豫东粉土)在干湿循环和不同压实度下的土-水特征曲线的试验研究尚未开展.笔者采用的是美国GCTS公司生产的土-水特征曲线固结仪，由Fredlund SWCC 装置和加载系统两部分组成.GCTS非饱和土固结仪通过轴平移技术控制基质吸力，试验中试样通过排水管与外界相连，它既可做非饱和土的压缩试验，也可作为压力板仪测定土-水特征曲线.

1 土样的基本性质与试样制备

1.1 土样的基本性质

土样取自豫东地区，取土深度约为3 m，主要物理力学性质指标如表1所示，颗粒分布曲线如图1所示.按照《公路土工试验规程》的分类，试验用土属于低液限砂质粉土.

表1 豫东地区粉土基本物理指标

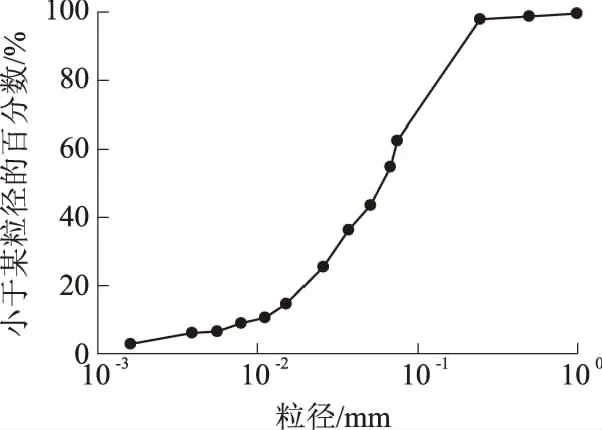
图1 豫东粉土的粒径分布曲线

1.2 试样制备

将土样碾压后过孔径2.0 mm的筛，烘干、冷却后配置成目标含水率的土样，密闭24 h；用静压实法将土样压制成标准的环刀样，初始高度为2 cm，直径为6.18 cm.在压实过程中，控制试样的压实度分别为90%、93%、96%，所对应的干密度分别为1.55、1.61、1.64 g/cm3.试样制成后用真空泵进行抽真空饱和，试样的初始状态见表2.

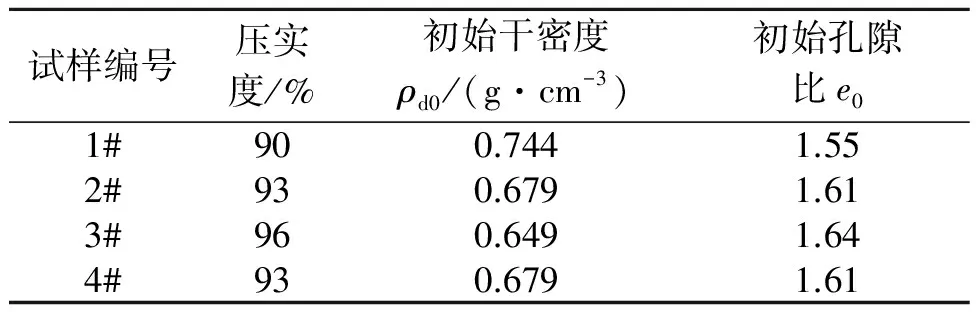
表2 试样的初始状态

1.3 试验方案

土-水特征曲线试验均是在净应力为0 kPa的状态下进行的.首先将制作的饱和试样装入GCTS 非饱和固结仪中，施加设定的吸力， 具体吸力路径如表3 所示.试样1#～3#分别进行了不同压实度下土-水特征曲线的脱湿和吸湿过程；而试样4#进行了3次控制吸力的脱湿和吸湿过程.

表3 吸力路径

2 试验结果及分析

2.1 压实度对土-水特征曲线的影响

图2为试样1#～3#的土-水特征曲线，其含水率、饱和度均随着吸力增加而降低，随着吸力降低而增加,由于“瓶颈效应”的存在，使脱湿曲线与吸湿曲线存在明显的滞回效应，脱湿曲线总是高于吸湿曲线.当吸力小于100 kPa时，土-水特征曲线的脱湿和吸湿曲线具有明显的滞回特性；当吸力大于100 kPa时，滞回特性不明显.

图2 不同压实度下豫东粉土的土-水特征曲线

图2(a)表明：随着压实度的增加，脱湿曲线和吸湿曲线均右向左下移动的趋势，即在吸力相同时，压实度小的比压实度大的试样含水率高.当吸力大于100 kPa，压实度对土-水特征曲线的影响不明显.Romero 和Vaunat[12]也获得了类似结果.由图2(b)可知，随着压实度的增加脱湿曲线和吸湿曲线均向右上方移动，即当吸力相同时，饱和度随着压实度的增大而增大，与Sun等[13]得到的试验结论类似.

2.2 干湿循环次数对土-水特征曲线的影响

图3为试样4#经历3次干湿循环的土-水特征曲线.用含水率-吸力表示和用饱和度-吸力表示，试样4#的含水率、饱和度均随着吸力增加而降低，脱湿曲线与吸湿曲线也存在明显的滞回效应.当吸力小于100 kPa时，脱湿和吸湿曲线具有明显的滞回特性；当吸力大于100 kPa时，其滞回特性不明显.

由图3可知：随着干湿循环次数的增加脱湿与吸湿曲线均向左下方偏移；滞回圈面积随着干湿循环次数的增加而减小.首次干湿循环对滞回圈大小影响较大，而干湿循环2、3次后的滞回圈变化不大，这与Ng 和Pang[9]、Ho 等[10]得到的试验结果类似.主要原因是反复干湿循环作用下土样孔隙内可能残存气泡，从而阻止水分进入孔隙，而孔隙内的气泡量趋于稳定[6]，这样逐渐减弱了干湿循环产生的影响；经过多次干湿循环后，孔隙结构趋于稳定，土-水特征曲线基本处于稳定状态，受干湿循环的影响小.

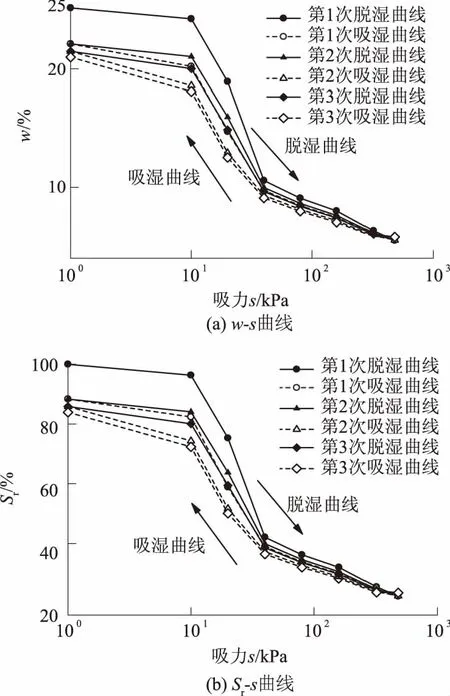
图3 豫东粉土经历多次干湿循环的土-水特征曲线

3 SWCC的曲线拟合及预测方法

用Van Genuchten模型[14]对粉土的实测土-水特征曲线进行了拟合.

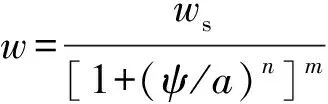
(1)

式中：w是吸力ψ对应的重力含水率；ws是饱和重力含水率；a、n、m是模型拟合参数.

3.1 不同压实度的SWCC的曲线拟合及预测

用Matlab中的Lsqcurvefit函数对试验数据进行拟合并得到Van Genuchten模型拟合参数，参见文献[15].不同压实度作用下的土-水特征试验数据点拟合的曲线见图4，拟合参数见表4.

从表4和图4可以看出，其拟合度均在98%以上，拟合效果良好.Van Genuchten模型中的拟合参数a、n均随着压实度的增加呈非线性增加；而拟合参数m随着压实度的变化不大.

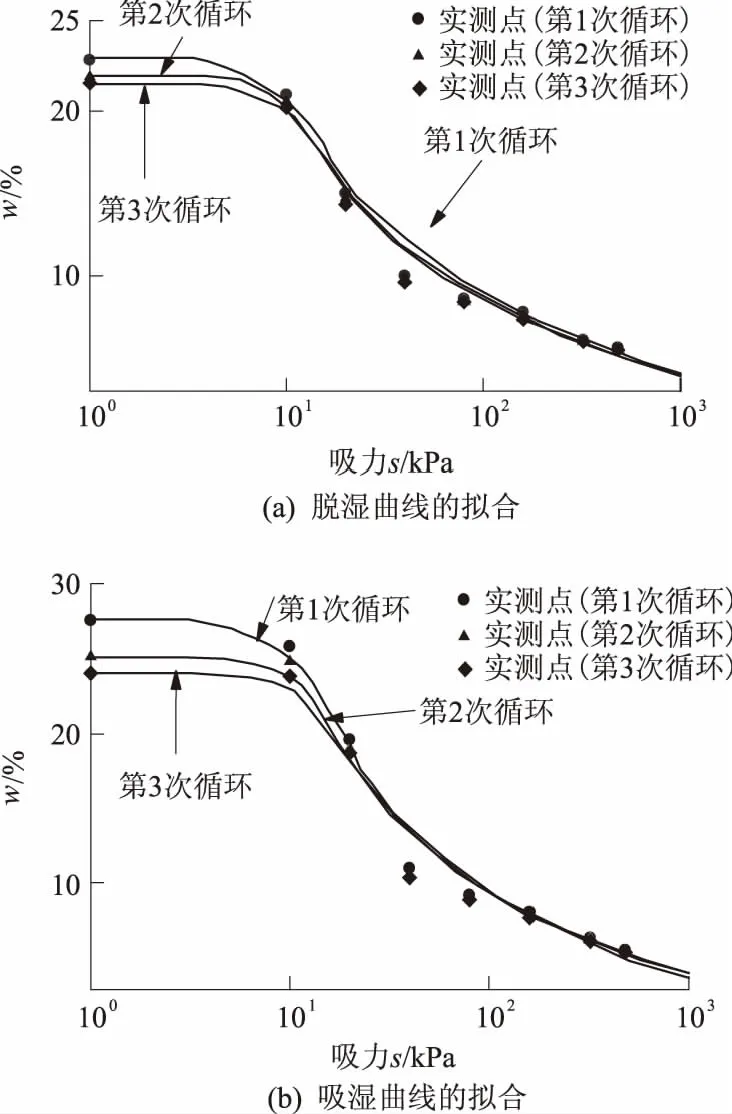
图4 不同压实度作用下土-水特征曲线的拟合

表4 不同压实度下试样的土水特征曲线的拟合参数

根据已知脱湿和吸湿曲线Van Genuchten模型中拟合参数随压实度的变化规律，建立与压实度有关的函数，具体表达式为：

ad=10.214d3.3158；

(2)

aw=0.123d1.076；

(3)

nd=0.203lnd+0.210；

(4)

nw=-0.002d2+0.112d-0.363.

(5)

式中：d为压实度；ad、nd为脱湿曲线拟合参数；aw、nw为吸湿曲线拟合参数.

将式(2)、(4)带入式(1)中，得到预测不同压实度下土-水特征曲线的脱湿曲线表达式为

(6)

(7)

根据公式(6)、(7)，可预测豫东粉土任意压实度的土-水特征的脱湿和吸湿曲线，如图4所示.

3.2 干湿循环多次的SWCC的曲线拟合及预测

用Matlab中的Lsqcurvefit函数对试验数据拟合得到Van Genuchten模型拟合参数.不同干湿循环次数的土-水特征试验数据点拟合的曲线如图5所示，其拟合的参数具体见表5.从表5和图5可知，拟合效果良好，Van Genuchten模型中的拟合参数a、n均随着干湿循环次数的增加呈非线性减小；而m随着干湿循环次数的变化不大.Van Genuchten模型中参数a与空气进气值有关，在反复干湿循环下，试样表面会出现些裂隙，气体进出导致试样的进气值减小.

根据已知脱湿和吸湿曲线Van Genuchten模型中拟合参数随干湿循环次数的变化规律，建立与干湿循环次数有关的函数，具体表达式为：

ad=0.347N2+49.92N-175.9;

(8)

aw=30.69e-0.53N;

(9)

nd=6.304e-0.04N.

(10)

图5 干湿循环时土-水特征曲线的拟合

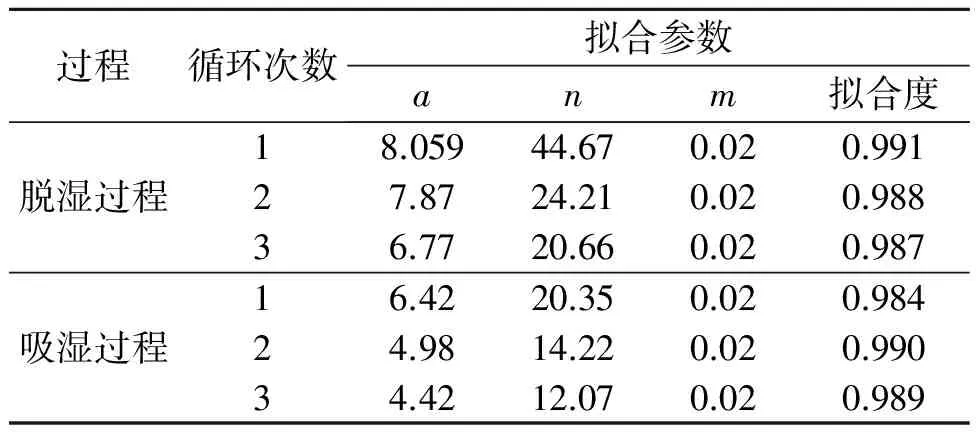
过程循环次数拟合参数anm拟合度18．05944．670．020．991脱湿过程27．8724．210．020．98836．7720．660．020．98716．4220．350．020．984吸湿过程24．9814．220．020．99034．4212．070．020．989

nw=13.35e-0.12N.

(11)

式中：N表示干湿循环次数.

将式(8)、(10)带入式(1)中，得到预测干湿循环多次土-水特征曲线的脱湿曲线表达式:

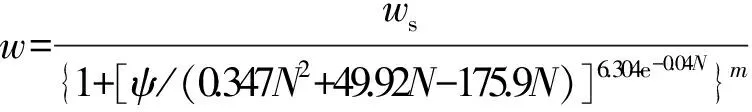
(12)

将式(9)、(11)带入式(1)中，得到预测干湿循环多次土-水特征曲线的吸湿曲线表达式:

(13)

根据公式(12)和(13)，可预测干湿循环多次的豫东粉土土-水特征曲线脱湿曲线和吸湿曲线.

4 结论

(1)豫东粉土的土-水特征曲线的脱湿和吸湿曲线具有明显的滞回特性，当吸力大于100 kPa时滞回特性不明显.土-水特征曲线用含水率和吸力关系表示时，含水率随着压实度和干湿循环次数的增大，脱湿和吸湿曲线均向左下方偏移；土-水特征曲线用饱和度和吸力关系表示时，脱湿和吸湿曲线随着压实度的增加均向右上方偏移，而随着干湿循环次数的增加向左下方偏移.

(2)脱湿与吸湿曲线间的滞回圈面积随干湿循环次数的增加而减小,首次干湿循环对滞回圈影响较大，而随后干湿循环对滞回圈影响很小.

(3)通过建立Van Genuchten模型的参数与压实度或干湿循环次数的函数关系，提出了可以预测不同压实度和干湿循环多次后的豫东粉土土-水特征曲线的方法.

[1] XU Y F, SUN D A. Determination of expansive soil strength using a fractal model[J]. Fractals, 2001, 9(1): 51-60.

[2] 王协群，邹维列，骆以道，等. 考虑压实度时的土水特征曲线和温度对吸力的影响[J]. 岩土工程学报, 2011, 33(3): 368-372.

[3] 张雪东，赵成刚，蔡国庆，等. 土体密实状态对土-水特征曲线影响规律研究[J].岩土力学, 2010, 31(5): 1463-1468.

[4] 汪东林，栾茂田，杨庆. 重塑非饱和黏土的土-水特征曲线及其影响因素研究[J].岩土力学, 2009, 30(3): 751-756.

[5] 叶灵敏. 干湿循环作用下非饱和粉土路基的工程特性研究[D].郑州: 郑州大学水利与环境工程学院, 2014: 28-37.

[6] 刘奉银，张昭，周冬，等. 密度和干湿循环对黄土土-水特征曲线的影响[J].岩土力学, 2011, 32(Z2): 132-136.

[7] 杨俊，童磊，张国栋. 干湿循环效应对风化砂改良膨胀土CBR特性影响研究[J].郑州大学学报(工学版)，2014, 35(2): 19-23.

[8] 乐金朝，李新明，乐旭东.钢渣稳定土的水稳性试验研究[J].郑州大学学报(工学版)，2010, 31(2): 18-21.

[9] NG C W W, PANG Y W. Experimental investigations of the soil-water characteristics of a volcanic soil[J].Journal canadian geotechnical, 2000, 37(6): 1252-1264.

[10]HO K M Y, TSE J M K, NG C W W. Influence of drying and wetting history and particle size on state-dependent soil water characteristic curves (SDSWCCs)[C]//Proc 3rd Asian Conference on Unsaturated Soils. Nanjing: Science press, 2007:213-218.

[11]张俊然，许强，孙德安. 多次干湿循环后土-水特征曲线的模拟[J]. 岩土力学, 2014, 35(3): 689-695.

[12]ROMERO E, VAUNAT J. Retention curve of deformable clays[C]//TARANTINO A, MANCUSO C.In experimental evidence and theoretical approaches in unsaturated soils. Rotterdam, Netherlands: Balkema.2000： 91-106.

[13]SUN D A, SHENG D C, SLOAN S W. Elastoplastic modelling of hydraulic and stress-strain behaviour of unsaturated compacted soils[J]. Mechanics of materials, 2007, 39(3): 212-221.

[14]VAN GENUCHTEN M T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils[J]. America journal of soil science society, 1980, 44: 892-898.

[15]谭晓慧，余伟，沈梦芬，等. 土-水特征曲线的试验研究及曲线拟合[J]. 岩土力学, 2013, 34(Z2):51-56.

Influence of Compaction Degree and Drying-wetting Cycle on the Soil Water Characteristic Curve of Yudong Silt

ZHANG Tao1,2, YUE Jinchao1, ZHANG Junran3

(1.School of Water Conservancy and Environment Engineering, Zhengzhou University, Zhengzhou 450001,China; 2.Architectural Engineering Department, Henan Vocational and Techinical College of Communications, Zhengzhou 451400,China; 3.Henan Province Key Laboratory of Rock and Soil Mechanics and Structural Engineering，North China University of Water Resources and Electric Power，Zhengzhou 450045，China)

A series of the soil-water characteristic curve (SWCC) tests for Yudong silt with different compaction degree and wetting-drying cycles were conducted by the pressure plate apparatus with the GCTS model. The test results showed that the SWCC curves had obvious hysteresis phenomenon during the drying and wetting cycles when the value of the suction was less than 100 kPa. While the value of the suction was greater than 100 kPa, the SWCC hysteresis phenomenon was not obvious. The SWCC was expressed by the relations between suction and water content, the SWCC curves have a shift to the bottom and left trend with the increase in the compaction degree and drying-wetting cycles. When the SWCC is expressed by the relations between suction and saturation, the SWCC curves had a shift to the top and right trend with the increase in the compaction degree, while the SWCC curves had a shift to the bottom and trend with the increase in the wetting-drying cycles. The Lsqcurvefit function of the Matlab was adopted for fitting of the SWCC curves to get the fitting parameters of the Van Genuchten model. Through the relations between the fitting parameters and the compaction degree or drying-wetting cycles, the practical methods were proposed to predict the Yudong silt SWCC with different compaction degree or drying-wetting cycles.

compaction degree; drying-wetting cycle; Yudong silt; soil water characteristic curve; prediction

2015-10-20；

2015-12-28

河南省交通运输厅科技计划项目(2014K44)；河南省教育厅科学技术研究重点项目(14B580001;16B580001)

乐金朝(1965—)，男，河南信阳人，郑州大学教授，博士，博士生导师，主要从事岩土工程及道路工程研究工作,E-mail：yuejc@zzu.edu.cn．

1671-6833(2016)06-0053-05

U416.1

A

10.13705/j.issn.1671-6833.2016.03.027