基于OpenSees的高阶非线性桁架单元开发及应用

张俊峰，高健利

(郑州大学 土木工程学院， 河南 郑州 450001)



基于OpenSees的高阶非线性桁架单元开发及应用

张俊峰，高健利

(郑州大学 土木工程学院， 河南 郑州 450001)

对于大跨度的空间桁架结构，准确模拟非线性状态后的力学行为非常重要.基于UL法的增量微分方程，详细推导了空间桁架单元考虑几何非线性的高阶刚度矩阵，通过OpenSees开放平台，开发了高阶非线性桁架单元，给出了单元的实现方式、静力和动力计算的TCL命令流程和迭代过程的非线性算法，通过几种桁架结构的非线性静力和地震作用下的非线性动力对比分析，表明采用本文方法实现的单元能够准确模拟桁架结构的强非线性性能.

空间桁架；几何非线性；高阶刚度矩阵；OpenSees；二次开发

0 引言

大跨度桁架结构的施工过程以及使用寿命期内的变形与内力都具有明显的几何非线性，需要精确的几何非线性理论，为此许多学者进行了大量研究，Bathe[1]、Crisfield[2]提出了几种解决几何非线性的单元微分方程；Greco等[3]提出了用节点坐标描述应变并用最小势能原理建立空间桁架的非线性有限元方程，但是这些方法的局限性在于仅适用于大位移、小应变问题，且列式复杂，Greco等[4]又在其基础上引入了Logarithmic应变修正了这一问题；Thai等[5]对同时考虑几何和材料非线性的空间桁架结构的后屈曲行为做了研究； Shi等[6]对同时考虑几何材料非线性的空间桁架结构的动力行为做了研究；喻莹等[7]提出了有限质点法分析空间桁架结构动静非线性问题的思路.这些研究分别从坐标系统、非线性有限元方程列法、结构的动力与静力等方面研究了几何非线性对空间桁架的影响，对研究桁架的非线性行为有十分重要的意义.但这些理论还不完善，并且在实现途径上是基于自编的程序，不便于推广应用，笔者用更新的拉格朗日方法、更新格林应变张量、第二Piola-Kirchhoff应力张量，详细推导了空间桁架高阶刚度矩阵，并在开源软件OpenSees平台上编制了相应的桁架单元，给出了实现过程和相应的非线性算法以及TCL命令流程，为大跨度桁架结构的非线性静力和动力分析提供了很好的实现方式和途径.

1 空间非线性桁架单元刚度矩阵

1.1 空间桁架非线性方程

在更新的拉格朗日增量分析中，用3种基本的构形来表示物体的运动状态：C0表示初始未变形的构形，C1是已知的参考构形，C2是变形后的构形.对于桁架来说，只考虑轴向变形，则更新的拉格朗日增量方程为[8]

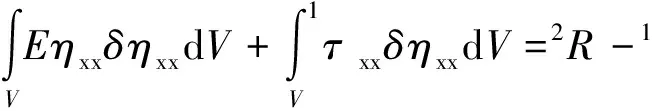
空间桁架单元的位移分量如图1所示，单元内任一点的位移(u，v，w)可以用形函数[N]来表示[8]：

(2)

图1 桁架单元的位移分量

格林应变增量可写成线性部分和非线性部分，εxx=exx+ηxx，将式(2)代入,得

(3)

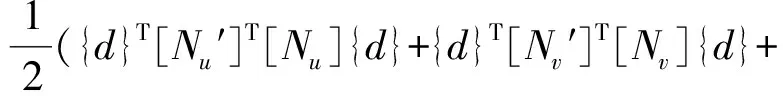
{d}T[Nw′]T[Nw]{d}).

(4)

假想单元节点只有集中荷载，而对于分布荷载可以用静力平衡节点荷载来代替.这样，将方程(3)和(4)代入(1)中,得

[Nv′]T[Nv′]+[Nw′]T[Nw′]){d}dV+

[Nv′]T[Nv′]+[Nw′]T[Nw′]){d}[Nu′]{d}dV+

[Nv′]T[Nv′]+[Nw′]T[Nw′]){d}{d}T+

([Nu′]T[Nu′]+[Nv′]T[Nv′]+[Nw′]T[Nw′])·

[Nv′]T[Nv′]+[Nw′]T[Nw′]){d}dV=

{δd}T({2f-1f}).

(5)

1.2 高阶非线性桁架单元刚度矩阵

利用虚位移原理，由(5)可以推出桁架单元的有限元方程为([ke]+[kg]+[s1]+[s2]+[s3]){d}+{1f}={2f}.

(6)

式中:{1f}为C1构形对应的初始力;{2f}为C2构形对应的总力.

由式(5)可得方程(6)中各刚度矩阵为

(7)

式中：[ke]是线性刚度矩阵；[kg]是几何刚度矩阵，由每个增量步的轴力P决定；[s1]和[s2]是与单元增量位移线性相关的矩阵；[s3]是与单元增量位移二阶相关的矩阵[9].

1.3 高阶刚度矩阵的对称形式

刚度矩阵的对称与否直接会影响到计算程序实现的效率.由式(7)得到的刚度矩阵[s1]和[s2]是非对称的，而矩阵[s1]和[s2]的和可以看作是[k1]/2，该矩阵是对称的[10].由式(7)和其组成部分对应的刚度矩阵可以看出：刚度矩阵[s2]和[s3]之和等效于[kg]矩阵，因此可以写出[s2]和[s3]的等效刚度矩阵[s2]eq和[s3]eq.由矩阵[s1]和[s2]的和减去[s2]eq就得到了[s1]的等效矩阵[s1]eq，从而刚度矩阵由原来的非对称形式转换成了对称形式.

2 高阶非线性桁架单元的开发与应用

2.1 高阶非线性桁架单元的开发

OpenSees(Open System for Earthquake Engineering Simulation)是应用于地震工程研究的开源有限元程序，由美国国家自然科学基金资助、太平洋地震工程研究中心研发，它是用面向对象的语言进行开发的，而且代码公开，因此可以协同开发新单元、新材料等[11].

为了校核并更加方便地使用推导的高阶桁架单元，基于OpenSees软件平台，在element基类上派生了nonlineatTruss3D类，并和uniaxialMaterial类关联，以方便调用uniaxialMaterial类的材料信息，该单元类参与模型的建立，并将模型添加到Domain类中，Domain类和Analysis类关联，从而完成整个分析过程.

2.2 TCL调用nonlinearTruss3D单元流程

OpenSees调用nonlinearTruss3D单元进行静力和动力分析的流程如图2所示，分析时采用Tool Command Language (TCL)语言进行建模、分析、输出.

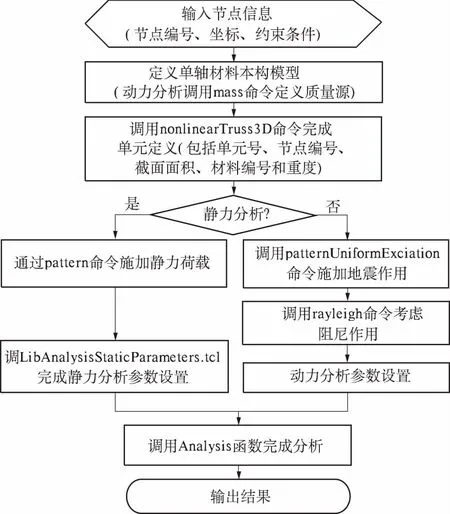
图2 OpenSees计算流程图

2.3 非线性分析算法

调用高阶非线性桁架单元nonlinearTruss3D进行非线性分析的增量迭代算法流程如图3所示.分析中，首先调用uniaxialMaterial类获得材料的切线刚度E，计算单元刚度矩阵Ke，组装形成结构的总体刚度矩阵Kg，某一荷载增量下，结构的完整非线性分析工作需要多次迭代，迭代结束的判断条件为总体结构不平衡力Pu足够小.

3 算例分析

为了验证开发的高阶非线性桁架单元nonlinearTruss3D在OpenSees平台上进行静力和动力分析的准确性，笔者对4个经典算例进行了数值模拟，包括平面和空间桁架的静力和动力分析.为了准确追踪其非线性行为，静力分析采用弧长法，动力分析采用Newmark直接积分和Newton-Raphson迭代结合算法.

3.1 六角星桁架静力分析

Thai等[12]对一个六角星桁架进行了分析，该桁架有24根杆件，所有杆件的截面面积A和弹性模量E都相同，A=0.1 cm2，E=2.034×107N/cm2，边缘假定为铰接.

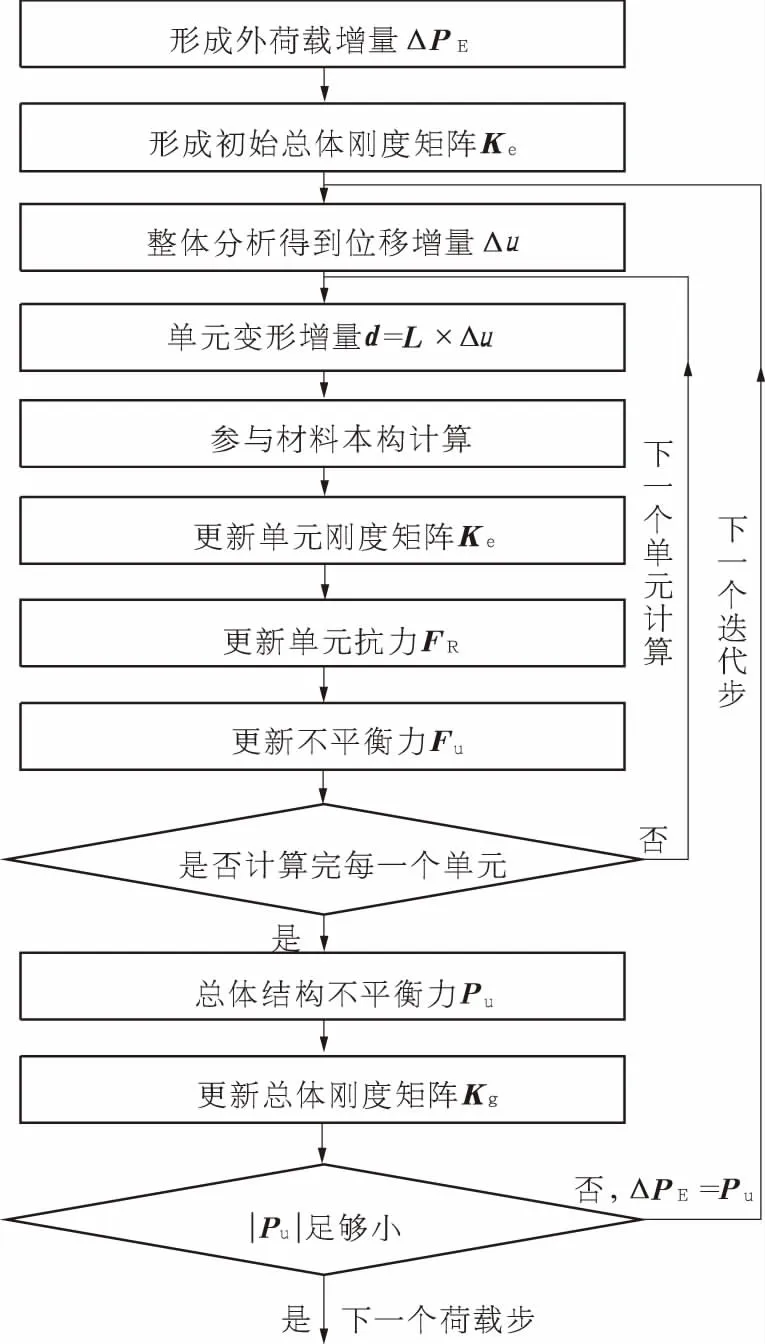
图3 增量迭代流程图

采用nonlinearTruss3D单元计算得到结构顶部节点的荷载-位移曲线，与文献[12]的对比如图4所示，两者相差不超过1%.

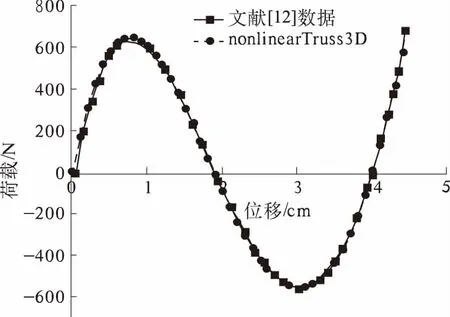
图4 顶部节点1竖向位移

3.2 测地圆顶桁架静力分析

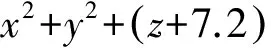
采用nonlinearTruss3D单元计算得到顶部节点的荷载-位移曲线，与文献[12]的对比如图5所示，二者相差不超过1%.

图5 顶部节点竖向位移

3.3 悬挂桁架动力分析

Thai等[13]对某悬挂桁架进行了分析，该桁架由两根相同的杆件组成，面积为A= 314.16 cm2，材料弹性模量E= 2.0×105MPa，自由节点的集中质量m= 5.0×104N·s2/mm，地震波采用EL-Centro波.

采用nonlinearTruss3D单元对该结构进行弹性时程分析得到自由节点的时程位移曲线与文献[13]的对比如图6所示.可以算出，二者最大相差不超过1%.

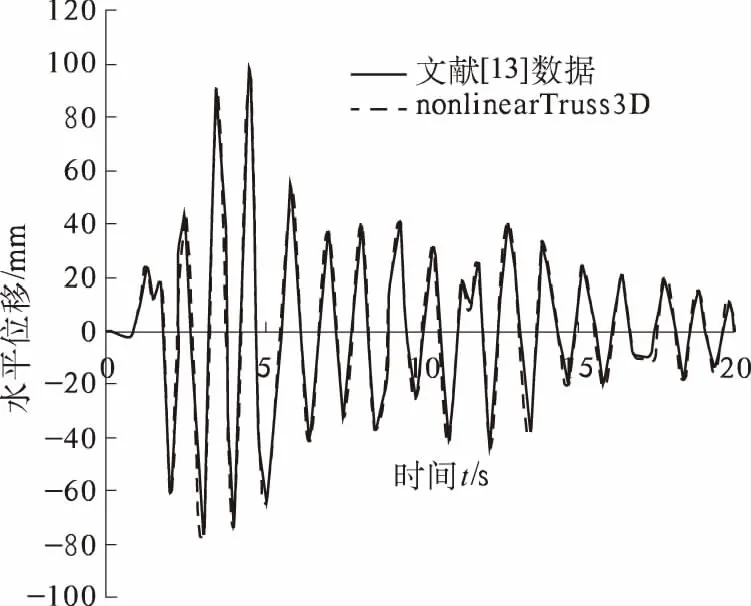
图6 自由节点的时程位移曲线

3.4 空间桁架动力分析

Thai等[13]对一单跨三层空间桁架进行了分析，竖向平面构件采用L5×5×5/16截面，水平面构件采用L4×4×1/4截面，弹性模量E= 200 GPa，每层的集中质量为m= 50 N·s2/mm，基底承受水平地震作用，地震波采用EL-Centro波.

用nonlinearTruss3D单元对该空间桁架进行弹性时程分析得到顶层节点的时程位移曲线，与文献[13]的对比如图7所示.

从图7可以得出，采用nonlinearTruss3D单元得到的空间桁架各层峰值位移和文献[13]的对比，相差最大不超过3%.

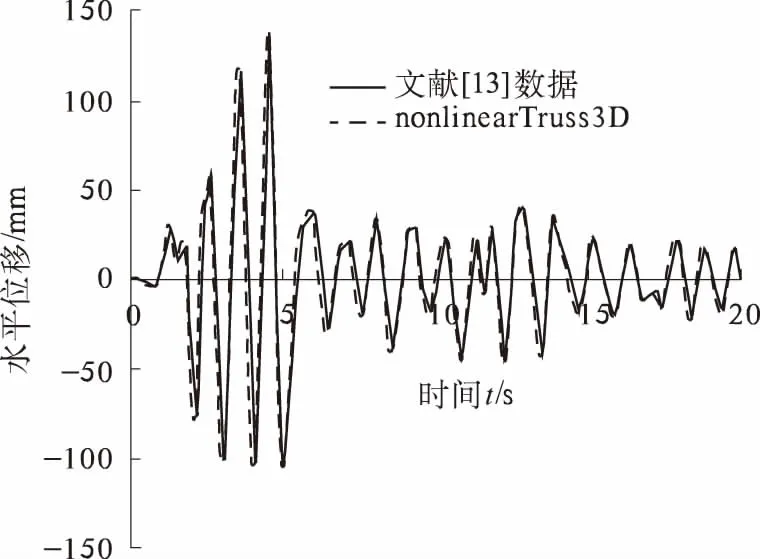
图7 顶层节点时程位移曲线

4 结论

(1)基于更新拉格朗日构形的增量虚位移原理推导出空间桁架单元的高阶非线性刚度矩阵.

(2)基于OpenSees软件平台，在element单元基类上派生了nonlinearTruss3D类，开发了高阶非线性空间桁架单元.

(3)基于OpenSees软件平台，给出了采用nonlinearTruss3D单元进行非线性静力和动力分析的模块化分析流程和增量迭代流程.

(4)通过4个平面和空间桁架结构算例的非线性静力和动力分析，验证了开发的nonlinearTruss3D单元具有很高的精度，可以很好模拟结构的非线性静力和动力反应.

[1] BATHE K J. Finite element procedures [M]. Upper Saddle River,NJ:Prentice-Hall, 1996.

[2] CRISFIELD M A. Non-linear finite element analysis of solids and structures [M].Mhichester West Sussex,England:John Wiley & Sons, 1991.

[3] GRECO M, GESUALDO F A R, VENTURINI W S, et al.Nonlinear positional formulation for space truss analysis [J]. Finite elements in analysis and design, 2006,42(12):1079-1086.

[4] GRECO M, FERREIRA I P. Logarithmic strain measure applied to the nonlinear positional formulation for space truss analysis [J]. Finite elements in analysis and design, 2009,45(10):632-639.

[5] THAI H T, KIM S E. Large deflection inelastic analysis of space trusses using generalized displacement control method [J]. Journal of constructional steel research, 2009, 65(10/11):1987-1994.

[6] SHI H, SALIM H, SHI Y, et al. Geometric and material nonlinear static and dynamic analysis of space truss structures [J]. Journal of mechanics based design of structures and machines, 2015, 43(1):38-56.

[7] 喻莹, 许贤, 罗尧治. 基于有限质点法的结构动力非线性行为分析[J]. 工程力学, 2012, 29(6):63-69.

[8] LEU L J, YANG Y B. Effects of rigid body and stretching on nonlinear analysis of trusses [J]. Journal of structural engineering, 1990, 116(10):2582-2598.

[9] YANG Y, KUO S. Theory and analysis of nonlinear framed structures [M]. Englewood Cliffs ,New Jersey:Prentice Hall, 1994.

[10]CHAJES A, CHURCHILL J E. Nonlinear frame analy-

sis by finite element method [J]. Journal of structural engineering, 1987, 113(6):1221-1235.

[11]MCKENNA F, FENVES G L . Introducing a new element into OpenSees [R]. Berkely:PEER, University of California, 2000.

[12]THAI H T, KIM S E. Large deflection inelastic analysis of space trusses using generalized displacement control method[J]. Constructional steel research, 2009, 10(11):1987-1994.

[13]THAI H T, KIM S E. Nonlinear inelastic time-history analysis of truss structures [J]. Constructional steel research, 2011, 67(12):1966-1972.

Development and Application of Higher Order Nonlinear Truss Element in OpenSees Platform

ZHANG Junfeng, GAO Jianli

(School of Civil Engineering, Zhengzhou University, Zhengzhou 450001,China)

For long-span space truss structures, it was very important to accurately simulate the nonlinear performance. Based on the increment of UL method of differential equation, the stiffness matrix of the space truss considering geometric nonlinear was deduced. The high order nonlinear truss element was developed in the OpenSees platform. The realization of the element, the static and dynamic calculation of TCL command flow and the nonlinear algorithm of iterative process were put forward. Several kinds of truss structure under the action of nonlinear static and seismic nonlinear dynamic analysis were carried out. And the results showed that the element could reflect the strong nonlinear behavior of trusses.

space truss; geometric nonlinear; higher order stiffness matrix; OpenSees; secondary development

2015-10-28；

2015-12-26

河南省科技攻关计划项目(142102310345)

张俊峰(1981—)，男，河南洛阳人，郑州大学讲师，博士，主要从事空间钢结构非线性研究，E-mail：zhangjunfeng@zzu.edu.cn.

1671-6833(2016)06-0063-05

TU375

A

10.13705/j.issn.1671-6833.2016.03.025