基于Bruggerman理论的双金属合金光学特性研究

范春珍，臧华平，牧凯军

(1.郑州大学 物理工程学院，河南 郑州 450001; 2.新乡医学院 第一附属医院，河南 新乡 453100)



基于Bruggerman理论的双金属合金光学特性研究

范春珍1,2，臧华平1，牧凯军1

(1.郑州大学 物理工程学院，河南 郑州 450001; 2.新乡医学院 第一附属医院，河南 新乡 453100)

双金属合金纳米颗粒基于杂化的表面等离子共振特性表现出优异的光学性能，因而利用Bruggerman理论研究双金属合金的光学调控特性，在准静态近似下计算双金属合金的光学消光系数、吸收系数、反射率和透射率，通过调节复合双金属合金的体积分数，体系的共振峰得到有效调节.结果表明，该研究方法是一种简单、快速、有效的方法，不需要求解复杂的微分方程，仅仅通过改变体积分数和颗粒周围的介电常数即可以实现光谱的调节.

双金属合金；表面等离子体共振；调控性；Bruggerman理论；反射率；透射率

0 引言

双金属合金纳米颗粒具有不寻常的化学和物理性质,在催化和生物分子检测领域中具有广泛的应用[1-3]，其优异的光学特性起因于表面等离子体共振的杂化.其中，表面等离子体共振是指在金属表面存在的自由振动的电子与光子相互作用产生的沿着金属表面传播的电子疏密波[4-9].双金属纳米颗粒的表面等离子体共振一般局限在两个单一组成分的共振峰之间[10]，并且这样的共振峰还取决于颗粒的组分、大小和形态.实验中经常利用化学还原法、微乳液法、激光烧蚀法等方法来制备新型双金属纳米颗粒.例如，文献[11]通过化学还原方法合成金银和金铜双金属纳米粒子并利用光谱分析其各种成分及其在表面增强拉曼散射中的应用，利用种子生长法可制备分层的核壳双金属金银纳米颗粒.文献[12]根据金和银的摩尔比率的不同,利用该类胶体获得苯硫酚和对巯基苯胺的表面增强拉曼信号.生物模板法合成双金属铁钴纳米复合材料也被系统地进行探讨与研究[13].理论方面,1908年Mie散射理论的提出是通过求解麦克斯韦方程组得到金属颗粒的消光谱，之后离散偶极近似法、有限元法都被用来分析颗粒的光吸收特性.

当外加光场入射到贵金属纳米颗粒表面时，如果外场光子频率与贵金属纳米颗粒的传导电子的整体振动频率相匹配时，纳米颗粒就会对光子能量产生很强的吸收作用，实验观察到的吸收光谱会发生很明显的吸收峰，根据光谱可反映一系列的化学信息，并广泛用于纳米颗粒的表征.如何快速有效地判断合成的双金属纳米颗粒结构是现在急需要解决的问题.因此，通过双金属合金纳米颗粒的实验结果与理论结果进行比较分析，进而能清晰明确地证明合成的双金属纳米颗粒的结构，给金银复合颗粒的表征提供了新的分析手段，因此对于双金属纳米粒子的光学特性的理论研究是非常有必要的.

笔者采用Bruggerman有效介质理论研究双金属合金纳米颗粒的光学调控特性，在准静态近似下计算双金属合金的光学消光系数、吸收系数、反射率和透射率.计算结果表明，通过调节复合纳米颗粒的体积分数,共振峰可以得到有效的调节.该类可调控的共振波长对于选择合适的激发波长进行拉曼增强的研究具有很好的指导意义.

1 计算方法

光学波段的贵金属纳米颗粒的复介电常数εm(ω)可以通过实验测量的反射谱进行计算并得到.金属的复介电常数εm(ω)通常可以表示为εm(ω)=εr(ω)+iεi(ω)，包含实部εr(ω)和虚部εi(ω).并且复折射率可以表示为N(ω)=n(ω)+iκ(ω)，其中n(ω)是折射率；κ(ω)为消光系数.复介电常数和复折射率之间的关系为εm(ω)=N(ω)2，因此可得

εr(ω)=n(ω)2-κ(ω)2.

(1)

εi(ω)=2n(ω)κ(ω).

(2)

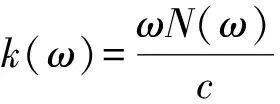
(3)

因此，吸收系数α(ω)与消光系数κ(ω)之间的关系为

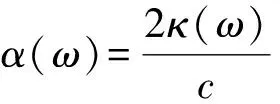
(4)

由此可见，吸收系数与消光系数成正比关系.

当光从一种介质传播到另一种介质时会发生反射和透射.根据电场在切向方向上的连续性以及电位移矢量在法向方向上的连续性，求解麦克斯韦方程组可得菲涅尔公式，反射系数R(ω)和透射系数T(ω)可表示为[14]

(5)

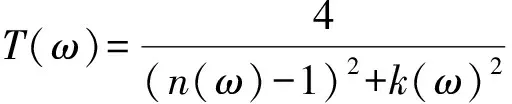
(6)

通常情况下，金属颗粒的介电常数表达形式可以通过求解谐振子运动方程得到德鲁得模型表示的形式.然而，考虑在特定波长下的介电性质时，为了将理论模型和实验数据进一步符合，需要添加洛伦兹修正项对德鲁得模型进行修正.笔者选取更为简便的德鲁得极限模型[14]，并且在可见光范围内与实验结果[15]得到有效的吻合.因此，贵金属颗粒的介电形式可表示为

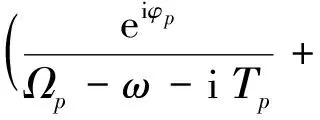
(7)

式中：ε为高频介电常数，即频率为无穷时的介电常数；ωp(ω)为等离子频率；γ为衰减因子；ω为外场频率；φp、Ωp、Ap为常数[14].

利用Bruggerman理论可以得到复合双金属纳米粒子的有效介电常数εe(ω).Bruggerman理论是一种对称理论，其所描述的两组元可以相互交换，不影响结果.并且该理论可以直接类比到多组分结构的复合颗粒.其表达形式如下：

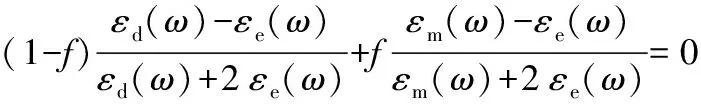
(8)

对于金银双金属合金纳米颗粒，选取f为贵金属银的体积分数；(1-f)为贵金属金的体积分数；εe(ω)为复合颗粒的有效介电常数；εm(ω)为金的介电常数；εd(ω)为银的介电常数.

2 结果与讨论

基于贵金属复合纳米颗粒的可控化学合成和表面等离子体共振光学特性的理论研究和实验研究表明，银颗粒通常在可见光区域内具有很大的活性，金颗粒在红外区域有很大的活性而近红外区活性有所降低，制备金银混合的纳米颗粒是两种金属活性的复合.依靠金属的特性选择一个合适的激发波长是很重要的，从而可以扩大这类复合金属纳米颗粒在表面增强拉曼散射中的应用范围.对于金属纳米颗粒而言，当入射光频率等于自由电子的集体共振的频率时候可以产生表面等离子体共振，此时在纳米颗粒的光谱结果中会出现该类材料的等离子体共振吸收峰如图1和图2 所示.金和银贵金属的介电函数在可见光范围内的主要特点为其实部均为负值，虚部值接近于零.这正是贵金属纳米粒子在可见光区域内具有特殊光学性质的主要原因，同时也是引起表面等离激元共振的必要条件.在可见光范围内，计算了波长从300～800 nm，单一贵金属金、银纳米颗粒的光谱特性，即金属颗粒的消光系数κ(ω)、吸收系数α(ω)、反射率T和透射率R，如图1～2所示.其中消光系数图中的小凹峰(a)与吸收系数中小的吸收峰(b)的位置相对应，表明金纳米颗粒在500 nm处发生共振(图1)，银纳米颗粒在340 nm 处发生共振(图2).金、银纳米粒子的吸收光谱是由金属粒子中电子的集体运动引起的表面等离子体共振吸收产生的.对于单一金纳米颗粒其反射率接近0.6，而其透射率很小，这也意味着具有较强的吸收，此时对应的波长在500 nm,如图1(c)和图1(d)所示. 图2 中计算了单一银纳米颗粒的光学特性，其结果和图1一致，银纳米颗粒具有较大的反射率，较小的吸收也发生在其等离子体共振峰的位置处.根据图1和图2 的计算结果可以发现，单一组分的贵金属纳米颗粒的消光系数、吸收系数、光散射与反射特性是由其表面等离子体共振决定的.

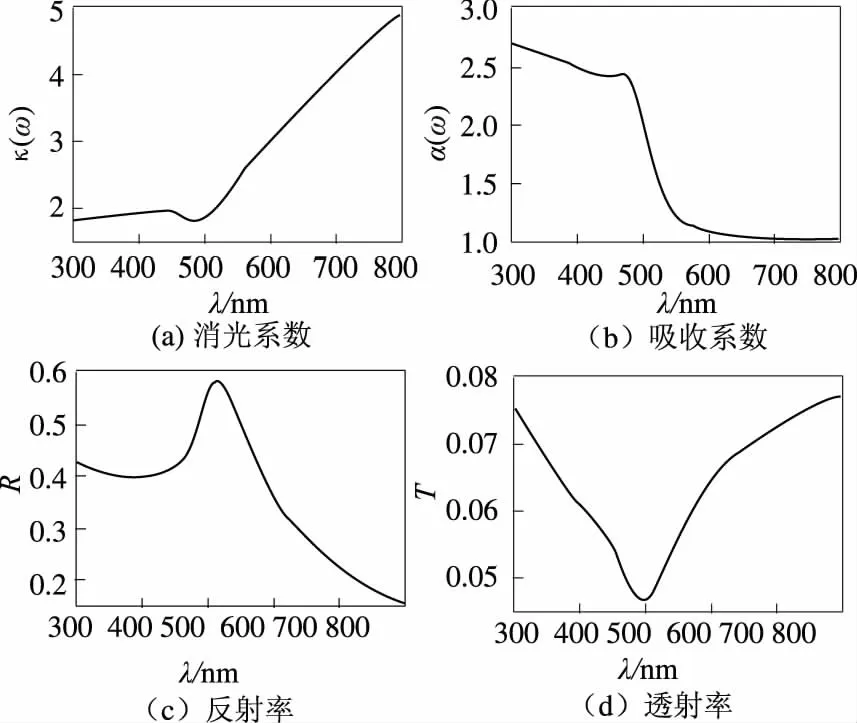
图1 金纳米颗粒的光学特性

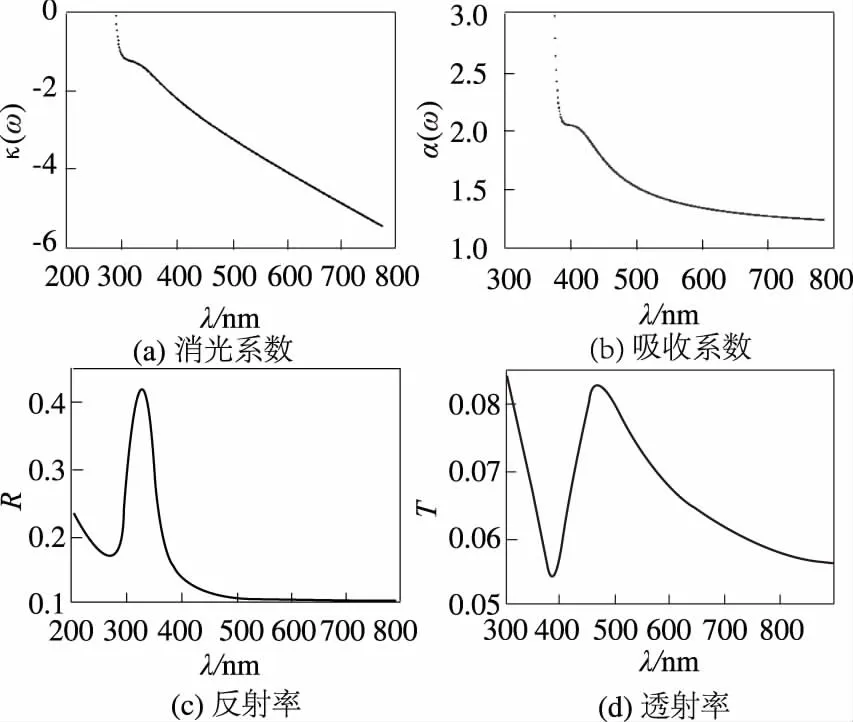
图2 银纳米颗粒的光学特性

对于双金属金银纳米颗粒的光学特性，计算结果表明：在300～800 nm波长内，体系存在两个吸收峰，其共振峰位置介于单个银、单个金颗粒吸收峰的之间(图3).随着组分比例的变化，金银合金纳米粒子的表面等离子体共振吸收峰会发生改变.该共振峰起源于金属表面自由电子的偶极震荡，并且当改变双金属合金中单一金属成分的体积分数时，其共振峰可以得到有效调节.其中，消光系数随着金属银的成分逐渐增多而增大，如图3(a)所示；而吸收系数随着体积分数的增大发生红移，且出现新的吸收峰，如图3(b)所示.最为显著的是，明显的双共振峰出现在反射率图3(c)和透射率图3(d)的光谱图中.当体积分数为0.15接近零时，双金属合金基本由银颗粒组成，其共振峰在340 nm处; 当体积分数从0.15逐渐增大到0.85接近1时，双金属合金由金组成，其共振峰在500 nm处.因此，我们可以发现，通过调节贵金属颗粒的体积分数，双金属合金的共振峰可以得到有效的调节.由于复合纳米颗粒的光学性质还受到其尺寸、形貌以及周围介电环境的影响，此时需要考虑其形状因子和结构尺寸，其光学特性同样可以得到有效调节.因此，双金属合金纳米颗粒等离子体共振峰位置的可控调节对于实验测得吸收光谱以及表面增强拉曼散射机理的分析都有着很重要的意义.

图3 金银双金属纳米颗粒的光学特性

3 结论

利用Bruggerman理论研究了复合颗粒的光学调控特性，在准静态近似下计算双金属合金的光学消光系数、吸收系数、反射率和透射率. 结果表明，当体积分数接近零时，双金属合金基本由银颗粒组成，其共振峰在340 nm处; 当体积分数接近1时，双金属合金由金组成，其共振峰在500 nm处； 金银合金颗粒的双共振峰介于340～500 nm，由金属粒子中自由电子的集体运动引起的表面等离子体共振吸收产生的.因此，通过调节贵金属颗粒的体积分数，双金属合金的共振峰可以得到有效的调节.该研究方法的创新在于不需要求解复杂的麦克斯韦方程组，能够快速有效地计算复合金属颗粒的光谱调节特性，并且可调节光谱波长范围，这对于双金属合金在表面增强拉曼散射中的应用即如何有效地选取激发波长提供了很好的指导意义.

[1] GOMES J F, GARCIA A C, PIRES C, et al. Impact of the AuAg NPs composition on their structure and properties: A theoretical and experimental investigation[J]. The journal of physical chemistry C, 2014, 118 (49): 28868-28875.

[2] TOSHIMA N, YONEZAWA T. Bimetallic nanoparticles-novel materials for chemical and physical applications[J]. New journal of chemistry, 1998, 22(11):1179-1201.

[3] CUI Y, REN B, YAO J L, et al. Synthesis of Ag core Au shell bimetallic nanoparticles for immunoassay based on surface-enhanced raman spectroscopy[J]. The journal of physical chemistry B, 2006, 110: 4002-4006.[4] MULVANEY P. Surface plasmon spectroscopy of nano sized metal particles[J]. Langmuir, 1996, 12(3): 788-800.

[5] BOHREN C, HUFFMAN D. Absorption and scattering of light by small particles [M]. New York:Wiley，1983

[6] GEHR J G, BOYD R W. Optical properties of nanostructured optical materials[J].Chemistry of materials,1996, 8(8): 1807-1819.

[7] FUCHS R. Theory of the optical properties of ionic crystal cubes[J].Physical review B, 1975, 11(4): 1732.

[8] ZHANG H, OKUNI J, TOSHIMA N. One-pot synthesis of Ag-Au bimetallic nanoparticles with Au shell and their high catalytic activity for aerobic glucose oxidation[J]. Journal of colloidal interface science, 2011, 354(1):131-138.

[9] COHEN R W, CODY G D, COUTTS M D,et al. Optical properties of granular silver and gold films[J]. Physical review B，1973, 8(8): 3689-3701.

[10]高继宁，任湘菱，唐芳琼.银/铂双金属中空纳米颗粒的制备及光学性质研究[J].感光化学与光化学，2006， 24(5)： 360-365.

[11]SRNOVA-SLOUFOVA B, VICKOVA B, BASTL Z. Bimetallic (Ag)Au nanoparticles prepared by the seed growth method:Two-dimensional assembling, characterization by energy dispersive X-ray analysis, X-ray photoelectron spectroscopy, and surface enhanced raman spectroscopy, and proposed mechanism of growth[J]. Langmuir, 2004, 20(8):3407-3415.[12]LIU X Y, WANG A Q, WANG X D, et al. Au-Cu alloy nanoparticles confined in SBA-15 as a highly efficient catalyst for CO oxidation[J].Chemical Communications, 2008, 27: 3187-3189.

[13]谢银德，侯保森，赵占中，等.生物模板法合成铁钴纳米材料的研究[J].郑州大学学报(工学版)，2015，36(6)：34-37.

[14]LAROCHE A VIAL T. Comparison of gold and silver dispersion laws suitable for FDTD simulations[J]. Applied physics B, 2008, 93: 139-143.

[15]JOHNSON P B, CHRISTY R W. Optical constant of nobel metals[J].Physical review B, 1972， 6(12):4370-4379.

Theoretical Calculations on the Light Behavior of Bimetallic Nanoparticles with Bruggerman Theory

FAN Chunzhen1,2, ZANG Huaping1, MU Kaijun1

(1.School of Physical Science and Engineering, Zhengzhou University, Zhengzhou 450052, China; 2.The First Affiliated hospital of Xinxiang Medical College, Xinxian 453100, China)

Bimetallic nanoparticles exhibied optical properties that differ significantly from those of the bulk material due to hybrid surface plasmon resonance. With the quasi-static approximation, the behavior of the light propagation was investigated. Resorting to the Bruggernan theory, the extinction coefficient, absorption coefficient, reflection, transmittance and refraction were theoretically investigated. Our results showed that by tuning the volume fraction of the metallic nanoparticles, its resonant peak could be tuned as accordingly. This calculation method can significantly improve the computing efficiency.

bimetallic nanoparticles; surface plasmon resonance; tunable; Bruggerman theory; reflection;transmission

2016-06-06；

2016-09-29

国家自然科学基金资助项目(11404290);河南省教育厅重点研究计划项目(15A140014)；河南省科技攻关计划项目(162102210164)

范春珍(1983—)，女，河南孟州人，郑州大学副教授，博士，主要从事于光学材料的特性研究，E-mail:chunzhen@zzu.edu.cn.

1671-6833(2016)06-0015-04

O 441.6

A

10.13705/j.issn.1671-6833.2016.06.0001