无向圆盘图中最大r跳独立邻居数的估计

周志诚，李翠静

(北京邮电大学，北京 海淀 100876)

无向圆盘图中最大r跳独立邻居数的估计

周志诚1，李翠静1

(北京邮电大学，北京 海淀 100876)

本文考虑无向圆盘图中的最大r-跳独立邻居数(2)r≥。给定一个圆盘图G=(V,E)，对任意vV∈，用()r NV

最大r跳；无向圆盘图；极大独立集；连通控制集

本文著录格式：周志诚，李翠静. 无向圆盘图中最大r跳独立邻居数的估计[J]. 软件，2016，37（11）：23-29

0 引言

在无线网络中，节点为了与其它节点进行通信，需要满足一定的连通性[1-3]，这种任务被称之为网络的拓扑控制[4]。受传统的有线网络物理骨干结构的启发，在无线网络中，引入虚拟骨干网络这一概念作为网络拓扑控制的手段来有效利用网络资源。于是，无线网络中如何构建虚拟骨干网成为关键。特别的，在无线传感器网络中，虚拟骨干网构造一般以连通控制集的思想来构造，随着研究的进一步深入，人们在此基础上考虑更一般的k连通r-跳控制集来作为虚拟骨干网。由此，如何构建规模小的k连通r-跳控制集就成为关键，近几年来受到很多学者的研究。

结合有向图强连通相关知识[5-6]，我们知道在现有的关于连通控制集和k连通r-跳控制集的构造算

法中一般都是先构造控制集满足控制要求，然后加入节点满足连通性要求，或者反其道而行之，先连通再控制[7-8]。在这些构建算法中，均以极大独立集的构造为基础。在分析算法的性能，即近似比时，需要用到每个节点的独立邻居数的最大值作为算法的近似比度量的重要部分。

在以往研究文献中，文献[9]给出了单位圆盘图上任何一个节点最多与5个相互独立的节点相邻，而后，文献[10-11]将其推广到一般圆盘图中，此时每一个节点最多与β个相互独立的节点相邻，其中K=1时，β=5；K取其它值时，K为圆盘图中最大圆的半径与最小圆的半径的比值。本文将上述结果推广到r跳情形，即任何一个节点其r跳邻居内的两两r-跳独立的节点的个数，得到一个最大r-跳独立数的较好上界。

本文结构如下，在第一节给出基本概念和介绍，在第二节给出主要结论及其证明，最后进行总结。

1 基本概念

定义1.2 极大独立集(maximal independent set)：子集U⊆V称为图G的独立集(independent set)，若U中任意两点都是不相邻的。若VU中任一点至少与U中一个点相邻，则称U为极大独立集。

定义1.3 控制集：图G=(V,E)的一个子集D⊆V称为控制集，若VD中任一点至少与D中一个点相邻，简记为DS。D中的节点称为控制节点（Dominator），VD的节点称为被控制节点(Dominated)。

如下图1中，黑色节点A，E，D表示控制节点，白色节点B，C，F表示被控制节点，从图中很明显可以看出，每一个白色节点都至少与一个黑色节点有边相连，即被黑色节点所控制。

图1 控制集

k-控制集dominating set) D定义为：D为V的子集，对任一点u∈(V/D)，u与D中至少有k个相邻节点，子集DV⊆称为k-控制集()kDS-。

若一个控制集D的导出子图是连通的，则称D为连通控制集 ()CDS；包含节点数最少的连通控制集称为最小连通控制集；若k-控制集D的导出子图是m-连通的，则子集D称为m-连通k-控制集。而k全控制集（k-totally dominating set）是指子集SV⊆使得对任意一个节点uV∈，u与 S中至少k个节点相邻。

定义1.4 r-邻居：给定图G=(V,E)，v∈V，u称为v的一个r-邻居，如果在G中存在一条长度至多为r的(v-u)路。记Nr(v)={u|u与v的距离最多为r}，称为v的r-邻域。

定义1.5 圆盘图：单位圆盘是一个半径为1的圆盘，用diskr(o)表示一个中心在o，半径为r的圆盘。一个图G=(V,E)称为单位圆盘图是指它可以嵌入到欧氏平面上，使得存在一条连接u与v的边e=(u,v)，且仅当disk0.5(u)∩disk0.5(v)≠Ø，换言之，u与v的欧氏距离d(u,v)≤1。

图G=(V,E)称为圆盘图是指它可以嵌入到欧氏平面上，使得存在一条连接u与v的边e=(u,v)，当且仅当u与v的欧氏距离d(u,v)≤min{r,t} 。

圆盘图是无线传感器网络的数学模型，每个传感器节点都有一个通信范围，以传感器节点为中心，通信范围为半径作圆，即形成欧氏平面上的一个圆盘。每个圆盘与传感器节点相对应。于是一个无线传感器网络与一个圆盘图对应，两个传感器节点可以通信当且仅当它们在各自的通信范围内，即两传感器之间的距离小于等于它们的传输半径。

下图2是一个无向的圆盘图实例。

图2 无向圆盘图

2 主要结论

引理2.1 在一个无向圆盘图中，每一个节点最

多与β个独立节点相邻，其中K为最大圆盘的半径与最小圆盘的半径的比值，当1K=时，5β=；K取其它值时，

定理2.1 在无向圆盘图G中，设rI是G的一个极大r跳独立集，则对于任意的顶点uG∈，(u)r N包含有rI中最多β个节点，这里(u)r N为u的r跳邻接集合，即为u，v之间的跳数，即连接u与v的最短路的边数，下同)，β定义如下，

令

下面我们用归纳法来证明定理2.1的结论：

图3为r=2时的一个实例，设最小圆盘的半径为Rmin=1，另一(大)圆盘的半径为R，且1＜R≤K。设x,y为点u的1-跳邻居节点，wi,wj为点u的2-跳独立节点，即vi,vj∈W。

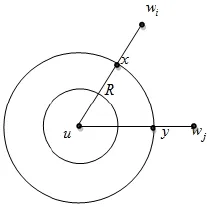
图3 无向圆盘图

由引理2.1知到对于1()Nu，最多包含个独立节点，若

离)，即h(x,y)=1，那么(wi,wj)-路径表示jP的反方向）的长度至多为这与矛盾，故结论得证。

图4 r=2时无向圆盘图的示意图

设A1，B1是属于1()Nu中的元素，A1，B1与点u之间的欧氏距离为1(,)duA，1(,)duB，且有设A2，B2是属于N2(u)中的元素，A2，B2与点u之间的欧氏距离表示为2(,)duA，

1）如果A2，B2为中的元素，那么根据的定义，A2，B2之间是3跳可达的，如下图5所示，设满足情况1）的中独立节点的个数为n1，下面估计1n的大小。

图5 r=2时无向圆盘图的示意图

假设d(u,A1)，d(u,B1)已经确定，A2，B2之间连边构成一个三角形，考虑临界情况，设角u大小为α，则只要比临界角小一点，A2，B2就不再独立的。显然，α越小，在圆盘图中就能够获得越多的这种独立节点，用αmin表示角度最小的情况，那么在圆盘图中最多有2παmin个2-跳独立节点，从而有：

下面来求最小的这种角minα。

图6 极限情况下构成的三角形

令d2=d(u,B2)，d3=d(u,A2)，则有2≤d2≤K+d1，2≤d3≤K+d1，由余弦公式可得：

注意到cosα在[0,]π中是单调递减的，要获得αmin，即要使得等式（2.3）的右边值最大。为此考虑如下规划

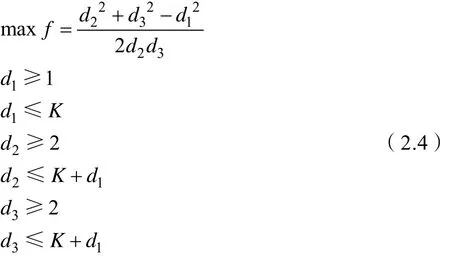
求minα的问题转化成求函数f在上面条件的限制下的极大值问题，我们利用KKT方程来求解，即拉格朗日函数。

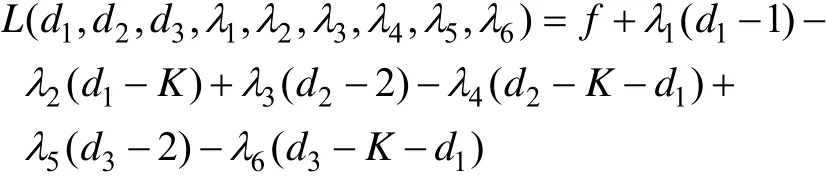
解KKT方程组（2.5）：

因为三角形还要满足其任意两条边之和大于第三条边，式（2.5）的解还必须满足条件（2.6），

通过计算求得满足（2.5-2.6）的所有点为：

将上述8个点依次代入（2.4）的目标函数中，其中最大的即为（2.4）的最优值，代入后可得目标值为如下三种情形：

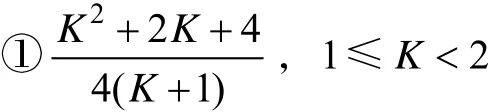
下面来讨论最大值。

（i）当12K＜≤时，①，②，③三个式子都成立，利用微积分判别法知，

当22K＜≤时有（4.5）的最优值为maxf=

（ii）当24K＜≤时，此时②，③两式可以成立，采用相减法判别②，③的大小，可知maxf=

（iii）当4K≥时，只有式②成立。

综上知

于是

2）假如A1，B2（或者A2，B1）为32T中的元素，如上图4为r=2时的无线圆盘图的示意图，那么根据的定义，A1，B2之间是3跳可达的，那么必然有A1，B1是相互独立的节点，设满足情况2）的独立节点的个数为2n.

若A1，B1是相互独立的节点，则内任意两个分别位于由u指向A1，B1方向的两条不同射线上A1及B1外的点g,h都是独立的(g在上，h在若有A2，B2属于则A1，A2不是2跳独立的，故与中的点不能同时存在，且由上图容易知道因此有，即n2=0，于是

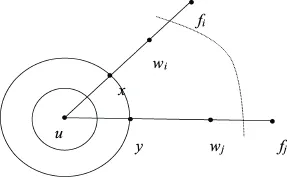
图7 r=3时无向圆盘图

设iw,jw是iuf，juf路上位于if，jf紧前的节点，则u到iw,jw是2跳的，且h(iw,jw)=4，否则

从而

由上面的结论，我们有

图8 r=3时的圆盘图

假设A3，B3是中的节点，那么A3，B3之间恰好经过4跳可相互到达，那么只可能是这样一种情况A1，B2（或A2，B1）之间有边相连，且A2，B2是两个2跳独立的节点，A1与B2独立，于是由前述证明知中元素的个数一定不大于中元素的个数，即

故

综上，

3 结论

本文主要是针对圆盘图上的邻居最大独立数进行了研究，得出了一个上界，利用该上界可以得到k-连通r-跳控制集构造算法的一个近似比。进一步的研究是改进此上界，另外，估计图的r-跳独立集大小和求解最大r-跳独立集也是很有意义的工作，它能用来指导虚拟骨干网构造算法的设计。

致谢

感谢编辑和审稿人的帮助和建议。

[1] 钱乐, 李文生. 基于S3C6410的多媒体传感节点的研究与实践[J]. 新型工业化, 2012, 2(8)∶ 33-40.

[2] 张朋, 周公博, 蔡志雄, 等. 双射频无线传感器网络节点硬件设计[J]. 新型工业化, 2013, 3(11)∶ 21-26.

[3] Zeng Jian, Jing Xiaojun, You Siqing.Research on Channel Modeling of Stratospheric Communication Systems[J]. The Journal of New Industrialization, 2011, 1(12)∶ 70-74.

[4] Xiuying Li, Zhao Zhang. 2010. Two algorithms for minimum 2-connected r-hop dominating set. Information Processing Letters 110∶ 22, 986-991.

[5] 吴金全. 有向图的强连通分量及应用[J]. 软件, 2014, 35(3)∶ 72-75.

[6] 郭衍奎, 胡俊, 徐晨光, 等. 一种基于极大连通子图的相关度属性选择算法[J]. 软件, 2014, 35(5)∶ 69-72.

[7] W. L. Wu, H. W. Du, X. H. Jia,et al Minimum connected dominating sets and maximal independent sets in unit disk graphs, Theor. Comput.Sci. 352 (2006) 1-7.

[8] D. Li, L. Liu and H. Yang, Minimum connected r-hop k- dominating set in wireless networks, Discrete Math. Algorithm. Appl. 1 (2009) 45-58.

[9] P. J. Wan, K. M. Alzoubi and O. Frieder, Distributed construction of connected dominating set in wireless ad hoc networks, ACM/Springer Mobile Netw. Appl. 9 (2004) 141-149. A preliminary version of this paper appeared in IEEE INFOCOM, 2002.

[10] D.-Z. Du, P.-J. Wan, Connected Dominating Set∶ Theory and Applications, Springer, 2013U. Erez and S. ten Brink, “A close-to-capacity dirty paper coding scheme,” Information Theory, IEEE Transactions on, 2005 51(10)∶ 3417-3432.

[11] P. J. Wan, L. Wang and F. F. Yao, Minimum CDS in multihop wireless networks with dis[arate communication ranges, in WASA (2010).R. Muharar, R. Zakhour and J. Evans, “Optimal power allocation and user loading for multiuser MISO channels with regularized channel inversion,” Communications, IEEE Transactions on, 2013, 61(12)∶ 5030- 5041.

Approximate Number of Maximum r-hop Independent Neighborhood Vertex of Disk Graph

ZHOU Zhi-cheng, LI Cui-jing
(Beijing University of Posts and Telecommunications, Beijing, 100876, China)

In this paper, we consider the maximum r-hop (2)r≥ independent neighborhood vertex of disk graph. Given a disk graph G=(V,E), let （）r NV be the set of vertices which distance is at most r-hop from v. For any

Maximum r-hop; Undirected disk graph; Maximal independent set; Connected dominating set

TN925+.3

A

10.3969/j.issn.1003-6970.2016.11.006

中国国家自然科学基金(11571044, 11471052)。

周志诚(1990-)，男，硕士研究生，主要研究方向：组合优化。李翠娟(1989-)，女，硕士研究生，主要研究方向：组合优化。

表示所有距节点v跳数最多为r的节点集合，则对G中任何一个r-跳独立集I，其在()r NV内最多有β个节点，这里K是圆盘图的最大圆盘半径与最小圆盘半径的比值.

independent set I of G, I have at mostvertices inHere K is a ratio between largest disk radius and smallest disk radius.