时滞对化学突触耦合的神经元网络放电节律的影响
赵竞哲,石 霞
(1. 北京邮电大学理学院,北京市 100876;2. 北京邮电大学理学院,北京市 100876)
时滞对化学突触耦合的神经元网络放电节律的影响
赵竞哲1,石 霞2
(1. 北京邮电大学理学院,北京市 100876;2. 北京邮电大学理学院,北京市 100876)
大脑中许多功能区可以呈现出不同形式的神经网络振荡活动,它们反映群体神经元的同步活动以及大脑的不同功能状态。高频节律反映的是大脑局部区域较快的信息处理,低频节律则能够反映外部的感觉输入和内部的认知事件的动态驱动在不同脑区的传播过程。这些不同形式的振荡活动分别在大脑处理、传递和整合感觉信息,巩固记忆,以及一些高级认知活动(如注意行为)中发挥重要的作用。其中,调整神经网络活动的振荡特性是实现这些脑功能的可能机制之一。本文发现突触的连接强度增大,可以加强同步。随着时滞的增大,在初始周期T的整数倍处,簇中spiking的个数会逐渐增加。神经元的频率会属于不同波段,且会出现混合振荡的状态。对于小的时滞,振荡是低频的。当时滞超过一定的值之后,网络从低频变为高频低频共存的状态,出现了混合振荡状态,并且这种转换快速且稳定。
时滞;HH神经元模型;可塑性;节律
本文著录格式:赵竞哲,石霞. 时滞对化学突触耦合的神经元网络放电节律的影响[J]. 软件,2016,37(11):09-13
0 引言
作为大脑活动节奏控制器的神经元同步,可以形成脑电波的某些频率[1],具有很重要的作用,并且有时神经元的同步会诱发一些如帕金森综合征等的疾病,因此关于脑电波频率的研究引起了很多学者的注意。
1924年,德国医生汉斯·贝格尔(Hans Berger)从一个颅骨受损的病人头部,检测到极为微弱的电流。随后又经过脑科学界几十年的研究成果,神经
科学界、国际脑波学会根据脑波频率将脑电波分成:δ 波[1,3] θ 波[4,7] α 波[8,13] β 波[14,30] γ 波[30,100]。这些不同形式的振荡活动分别在大脑处理、传递和整合感觉信息,巩固记忆,以及一些高级认知活动(如注意行为)中发挥重要的作用。其中,调制神经网络活动的振荡特性是实现这些脑功能的可能机制之一。
在大多数的物理和生态系统中,时滞是普遍存在的。它主要来源于信号有限的传播速度。由于时滞的出现,使得有限的动力系统变为无穷维的系统,从而诱导了更为复杂的非线性动力学特性,因此时滞耦合系统的非线性动力学行为引起了很多学者的关注。Ramana等人研究了时滞耦合的两极限环的动力学行为。Rossoni等人研究了具有时滞和类脉冲作用的两个耦合的 Hodgkin-Huxley神经元的发放行为。研究表明在时滞的作用下,两耦合神经元可以达到振荡消失现象和在同步等丰富的发放模式[2]。这些研究充分说明了时滞在耦合神经系统中有着重要的作用。
真实的神经系统通常都是动态的,因此我们不仅要考虑神经元动力系统和神经网络拓扑结构的高度非线性和复杂性,还要讨论神经网络系统的时变性、鲁棒性和易损性等问题,其中涉及的一个重要问题是学习和记忆功能,这与突触可塑性[3-8]研究密切相关。
本文的目的是研究突触可塑性参数对神经元发放和频率的影响。我们选取了HH模型[9-11],因为从生理学研究的角度,它是量化描述电生理现象很成功的一个模型。并且从非线性动力学和数学研究角度,其具有多变量、高度非线性和强耦合的特点。在本文中,我们首先建立了簇放电的神经元模型,然后研究了在神经元系统中,神经元的放电模式。最后我们探究了神经元节律的变化。
1 神经元模型
大脑神经网络的神经元按照形态和功能一般可分为谷氨酸能的椎体细胞和γ-氨基丁酸能的中间神经元[12]。其中中间神经元主要分布在局部脑区内部,对局部脑区的神经网络进行调节[13]。大量研究表明,中间神经元对大脑振荡模式的产生及知觉、睡眠、记忆等相关功能都有重要作用[14]。
本文使用的是全局耦合的HH神经元模型,每个中间神经元都满足下列动力学方程。

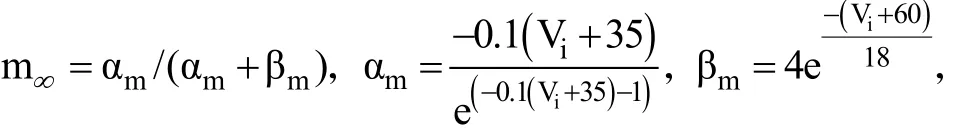
其中,σ是最大突触电导;ija是连接矩阵,如果神经元i和j相连则为1,否则为0。synE为逆转电位(如果synE足够小,例如为-80 mV,则突触为抑制性的;如果synE足够大,例如为0 mV,则突触为兴奋性的)。

我们使用通过可塑性化学突触耦合的神经元网络,其中网络为全耦合的抑制性中间神经元网络,经计算神经元的初始为0时)平均周期(神经元两次发放的平均时间间隔)T大约为10 ms。神经元数目为100,在[1,2]之间随机取值,实验模拟时间为1500 ms。
2 结果
我们首先研究中间神经元网络的同步与放电行为。图1展示了在没有突触后电流时,神经元的放电是混乱的。
我们可以看到随着时滞d的增大(图2),时空放电图的“放电带”越来越宽,我们随机去其中一个神经元画出其膜电位图,发现随着d的增加,神经元产生簇放电并且簇宽逐渐变大,每个簇间“尖峰”的个数在逐渐增多。
有趣的是,在数值结果中我们发现,簇间“尖峰”的个数的增多呈现出一定的周期性(图2未显示出)。

图1 突触后电流为0时,中间神经元网络的发放状态Fig.1 The state of the interneuron network when postsynaptic current is 0

图2 抑制性突触时滞d不同时,神经元的时空放电图和与之对应的膜电位图。时滞从上到下分别为10、30、60(ms)时,神经元网络的放电与神经元的膜电位变化。其他参数为σ0.3=Fig.2 The spatiotemporal pattern of neurons and the corresponding membrane potential maps with different delay.The delay from top to bottom are respectively 10, 30, 60 (ms). Other parameter for σ0.3=
为了更好的观察这一现象,我们研究了在取不同的σ时,随着时滞的逐渐增大,每个簇间“尖峰”个数的变化。当σ的值比较小时,几乎没有规律,但是当σ大于某个值之后,每个簇间“尖峰”(spiking)个数呈现出一定的规律性,尤其是在σ>0.1后变化基本相同,我们惊奇的发现,个数的增加大约出现在初始周期T的整数倍处,如图3所示。
时滞delay变化是簇中spiking个数图(σ >0.1后变化基本相同)可以看出在T的整数倍,个数会逐渐增加如图3所示。
除了研究簇中spiking个数的变化,我们还观察了单个神经元的频率与时滞d的关系。随着时滞的增大,神经元的振荡频率会属于不同波段,并且存在低频和高频两个区域,如图5所示。
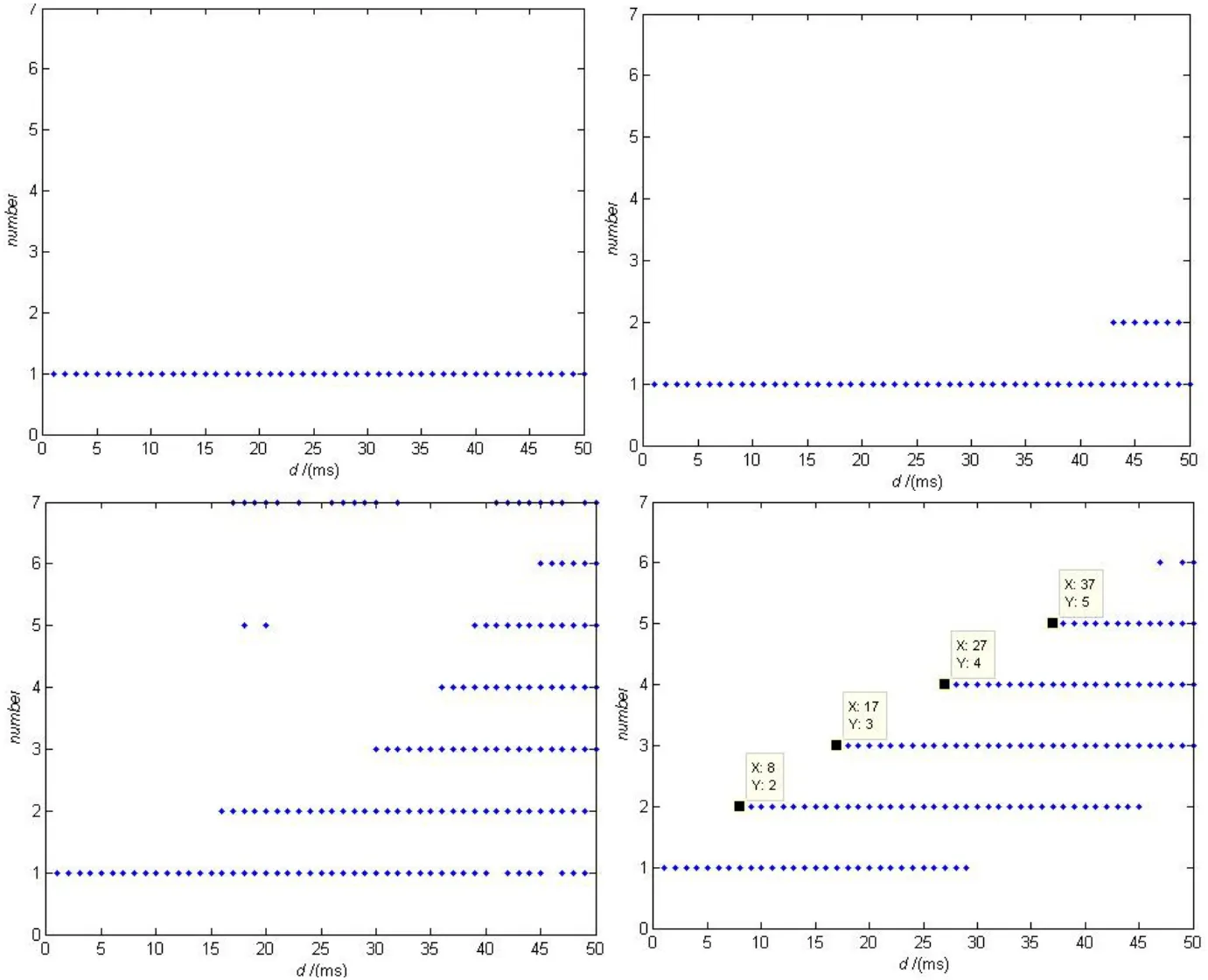
图3 不同σ随delay变化,一个周期内簇中spiking数的变化。σ的取值分别为0.005、0.01、0.02、0.05Fig.3 The number of spikes in one burst on delay with different σ. The value of σ is 0.005、0.01、0.02、0.05

图4 σ>0.1之后簇中spiking个数图Fig.4 The number of spikes in one burst on delay after σ>0.1
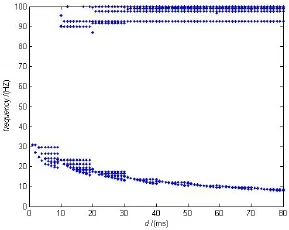
图5 单个神经元的频率变化。其中参数σ=0.3Fig.5 The change of frequency in single neuron
对于小的时滞(delay)d区域,振荡是低频的。当时滞d超过一定的值cd之后,网络从低频变为高频低频共存的状态,出现了混合振荡状态。这种转换快速且稳定。当时滞τ较小时,抑制性突触电流在一个周期内衰减较快,因此它们会在下一个循环的神经元放电之前消失,不会对下一个神经元放电产生影响。此时cd为10 ms,并且每次循环簇中spiking个数会每隔10 ms增加一个。也就是高频振荡的频率大约在100 HZ左右。
对于较长的时滞(delay),一个周期内的突触抑制性电流会延续到下一个周期。这些延续到下一周期的抑制性突触电流会抑制神经元放电,促使周期之间增大,这也就造成了低频频率在逐渐减小的现象。对于足够大的时滞(delay),神经元的频率会维持在 α 波段。混合的 α 和 γ 节律会在脑认知功能中起重要作用。高频节律反映的是大脑局部区域较快的信息处理,低频节律则能够根据外部的感觉输入和内部的认知事件动态驱动不同脑区的传播过程。传统的观点认为具有快和慢抑制性突触的神经元网络是形成特殊类型振荡的基本条件,但是我们的结果提供了一个全新的视角,我们发现长的时滞也会导致混合振荡。
3 结论
本文主要研究时滞对通过可塑性化学突触耦合
的神经元网络放电节律的影响。我们发现突触的连接强度增大,可以加强同步。随着时滞的增大,在初始周期T的整数倍处,簇中spiking个数会逐渐增加。接着我们关注时滞对神经元的放电节律影响。随着时滞的增大,神经元的频率会属于不同波段,且会出现混合振荡的状态。对于小的时滞,振荡是低频的。当时滞超过一定的值之后,网络从低频变为高频低频共存的状态,出现了混合振荡状态。这种转换快速且稳定。对于足够大的时滞(delay),神经元的频率会维持在 α 波段。混合的 α 和 γ 节律会在脑认知功能中起重要作用。传统的观点认为具有快和慢抑制性突触的神经元网络是形成特殊类型振荡的基本条件,但是我们的结果提供了一个全新的视角,我们得到的结果对研究神经元的节律及其控制有一定的参考作用。
[1] Wang X J Neurophysiological and computational principles of cortical rhythms in cognition, Physiological Reviews, 2010, 90∶ 1195.
[2] ROSSONI E, et al. Stability of synchronous oscillations in a system of Hodgkin-Huxley neurons with delayed diffusive and pulsed coupling. Physical Review E, 2005, 71∶ 061904.
[3] ABARBANEL, H, HUERTA R, RABINOVICH M I. Dynamical model of long-term synaptic plasticity. Proc. Natl. Acad. Sci. U.S.A.2002, 99, 10132-10137.
[4] BLAIS B S, COOPER L N, Shouval H Z Effect of correlated lateral geniculate nucleus firing rates on predictions for monocular eye closure versus monocularretinal inactivation. Phys. Rev. E Stat. Nonlin. SoftMatter Phys. 2009, 80, 061915-1-9.
[5] Amitai Y, FRIEDMAN A, CONNORS B W, GUTNICK M J Regenerative activity in apical dendrites ofpyramidal cells in neocortex. Cereb. Cortex 1993, 3, 26-38.
[6] Bi G Q, Poo M M. Synaptic modificationsin cultured hippocampal neurons∶ dependence on spike timing, synaptic strength, and postsynaptic celltype. J. Neurosci. 1998,18, 10464-10472.
[7] APPLEBY P A, ELLIOTT T. Synaptic and TemporalEnsemble Interpretation of Spike-Timing-Dependent Plasticity. Neural. Comput. 2005, 17, 2316-2336.
[8] BLAKEMORE C, COOPER G F. Development of the brain depends on visual environment. Nature1970, 228, 477-478.
[9] HODGKIN A L, HUXLEY A F. Currents carried by sodium and potassium ions through the membrabce of the giant axon of Lologo, J.pjysiol. 1952, 116∶ 449-472.
[10] HODGKIN A L, HUXLEY A F .The compontents of membrance conductance in the giant axon of Lologo, J.pjysiol. 1952, 116∶ 473-496.
[11] HODGKIN A L, HUXLEY A F. A quantitative description of membrane and its application to conduction and excitation in nerve. J.pjysiol.1952, 116∶ 500-544.
[12] HALASY K, SOMOGYI P Subdivisions in the multiple GABAergic innervation of granule cells in the dentate gyrus of the rat hippocampus. Eur J Neurosci, 1993.5(5)∶ p.411-29. [13] MARSHALLS L, et al. Hippocampal pyramidal cell-interneuron spike transmission is frequency dependent and responsible for place modulation of interneuron diacharge. J Neurosci, 2002. 22(2)∶ p.RC197.
[14] MOSER E I. Neurobiology∶Interneurons take charge. Nature, 2003. 421(6925)∶ p.797-9.
The Effects of Delay on Oscillations Rhythm of Neuron Network With Inhibitory Synapses
ZHAO Jing-zhe, SHI Xia
(Beijing University of Posts and Telecommunications, Beijing 100876, China)
Many functional areas of the brain can exhibit different forms of oscillatory brain activity, which reflect the synchronous activities of the group of neurons and the different functional states of the brain. The high frequency rhythm reflects the information processing of the local area of the brain. The low frequency rhythm is able to reflect the external sensory input and the internal cognitive events of the dynamic drive in different brain areas of the communication process. These different forms of oscillatory activity play an important role in brain processing, transmission and integration of sensory information, consolidation of memory, and some advanced cognitive activities (such as attentional behavior). Among them, adjusting the oscillation characteristics of neural network activity is one of the possible mechanisms to achieve these brain functions. Synchronization is enhanced as the synaptic connection increases. With the increasing of delay in the integer times the initial cycle of T, the number of spiking in one cluster will gradually increase. In particular, this paper have shown that short inhibitory delays could cause regular spiking, while a sufficiently long delay may lead to the appearance of mixed oscillations.
Delay; Hodgkin-huxley model; Synaptic; Oscillations rhythm
TN911
A
10.3969/j.issn.1003-6970.2016.11.003
国家自然科学基金(11272065)
赵竞哲(1991-),女,研究生在读。
石霞(1975-),女,副教授,复杂网络的非线性动力学研究。

