一种基于端点非插值性的NURBS曲面重构方法
张国军 幸 研
(东南大学机械工程学院, 南京 211189)
一种基于端点非插值性的NURBS曲面重构方法
张国军 幸 研
(东南大学机械工程学院, 南京 211189)
为了解决多面片拼接曲面、多修饰特征曲面连续性差且难以延展的问题,提出了基于端点非插值性的NURBS曲面重构方法.首先根据位置和曲率的不同,将原始曲面离散为点云数据,根据离散点计算各个采样路径上的节点矢量;然后计算出曲面重构所需的端点非插值性的共同节点矢量及相应的控制点,并将共同节点矢量转化成标准的端点插值节点矢量,根据最新的端点插值节点矢量在无数据点区间插入新的型值点;最后将所有数据点重新拟合成单一曲面.重构结果表明,通过使用该方法重构所需的计算量降低,重构出的曲面精度较高.在曲率变化剧烈处,既保证了与原始曲面的贴合率,又保证了截面线的曲率连续性.该方法将原始曲面重构为单一曲面,提高了曲面重构精度,有效地解决了造型中易出现的曲面退化、曲面畸变等问题.
非均匀有理B样条;曲面离散;曲面重构;端点非插值性
非均匀有理B样条(non-uniform rational B-spline,NURBS)在数学和算法上具有良好的性质,为解析曲线曲面和自由型曲线曲面的表示提供了一种统一的数学方法,在CAD领域中已成为表示曲线曲面的标准[1-2].
在工程应用中,绝大部分模型具有复杂的曲面结构,在建模过程中用一张曲面来表达复杂的外形特征比较困难,设计者为满足曲面之间边界的连续性,往往采用多张曲面或者对曲面进行桥接等操作来展示其复杂的外形特征.这样的拼接曲面在后续的操作过程中容易出现曲面畸形和曲面边界退化等问题.因此,需要对原始曲面进行重构,构造出单张连续的NURBS曲面.
很多学者对空间曲面的重构进行了大量的研究.Hu等[3]将NURBS的端点非插值性应用于曲线和曲面的外插延伸;Chen等[4]应用端点非插值性实现三次B-spline曲线的逼近.这些算法都是在节点矢量端点插值的基础上向前(后)插值构造出新的节点矢量,新的节点矢量都是基于单条曲线的非端点插值矢量且突破了原有曲线边界,并没有考虑与其他曲线节点矢量之间的关系,即在NURBS曲面重构中,各截面线不仅有轮廓界限,而且要具备共同节点矢量.由于大多数原始曲面的边界并不规则,导致重构过程中所需的截面线的次数p不完全相同,节点矢量也不完全相同,因此需要对这些截面线进行处理,以获取共同节点矢量.
本文应用NURBS节点矢量端点非插值特性,提出了一种更快、更高效的共同节点矢量确定方法,在充分考虑到各截面线的节点矢量信息的同时,对共同节点向量进行插值性转换[5],实现原始曲面的NURBS重构.
1 NURBS曲线曲面和德布尔算法
定义一条p次NURBS曲线为
(1)
式中,Pi为控制点,可形成控制多边形;ωi为权因子;Ni,p(u)为定义在非周期节点矢量u上的p次B样条基函数,可以根据德布尔算法[1](de Boer algorithm)来计算[1,6],即
(2)
2 NURBS曲面重构
曲面重构是基于B样条插值曲线与蒙皮曲面的拟合,利用一张光滑的曲面拟合原始拼接曲面,使其具有良好的几何建模性能.本文提出的基于端点非插值性的重构方法流程如图1所示.
2.1 节点矢量的端点非插值性与端点插值性
节点矢量分为端点插值和端点非插值[7].p次m+1个节点向量通常表示为
(3)
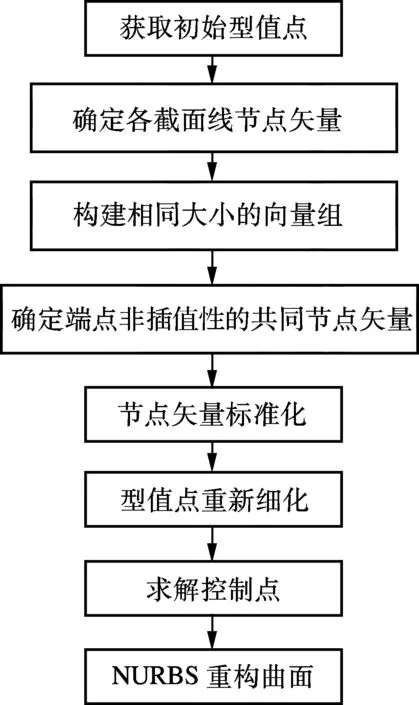
图1 曲面重构流程
对于端点插值节点矢量,第一个和最后一个节点重复度等于曲线的阶数;而非端点插值节点矢量,第一个和最后一个节点重复度不等于曲线的阶数.
2.2 基于端点非插值性的共同节点向量的确定
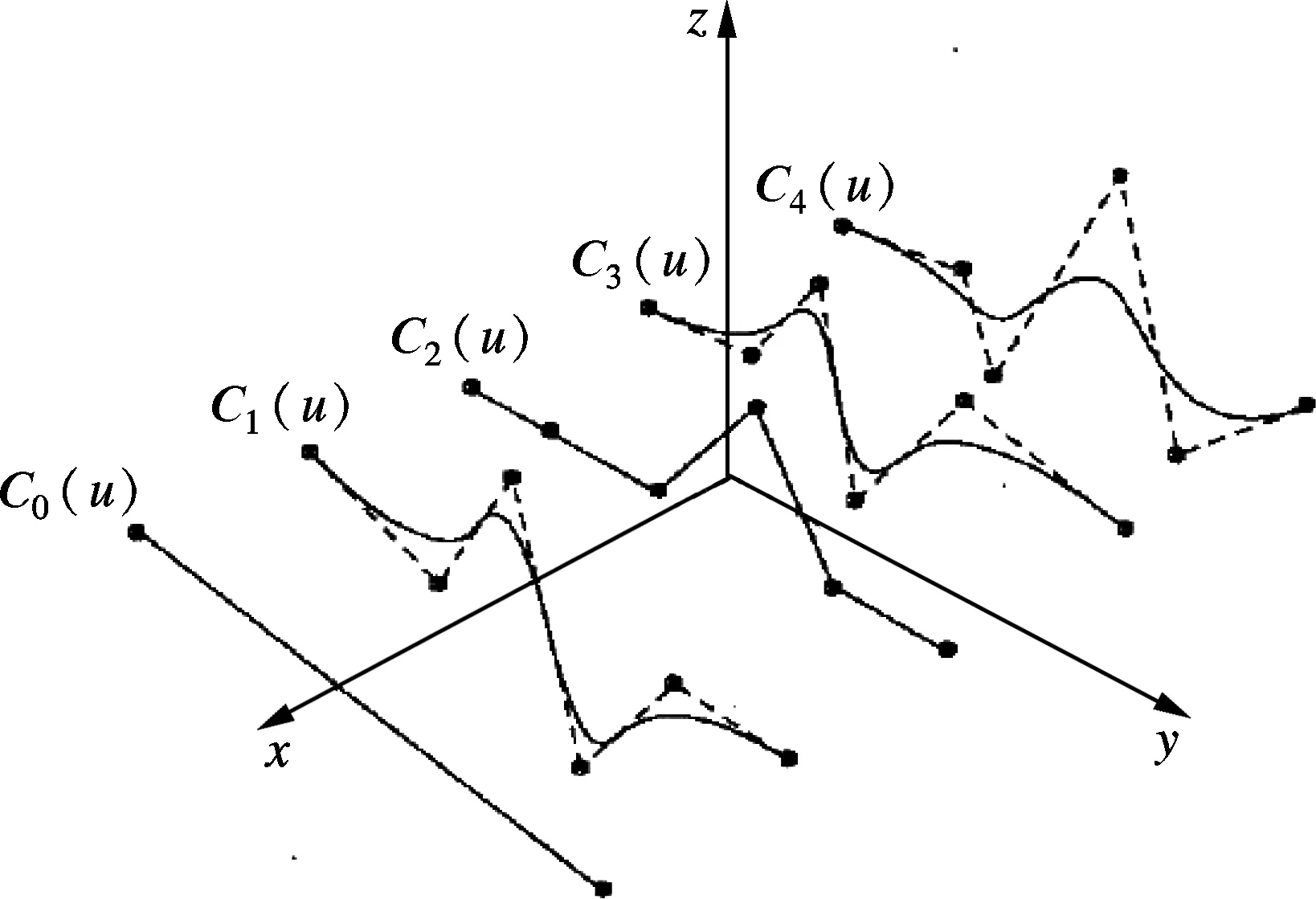
曲面一般都具有复杂的外形,往往是由多张曲面拼接而成,而且面片之间进行了复杂的裁剪、平移等操作.在实际操作过程中,由于各个面片轮廓复杂且阶数不同[8],当在给定边界上沿不同路径获取曲面离散点时,各个路径可能会通过一个或者多个面片;另外由于曲面边界的不规则,不同路径上离散数据点的数量也会有差别, 如图2(a)所示.当2条采样路径距离很小时(即通过相同的面片),采样路径曲率大小不同,使采样点数量出现差异,如图2(b)、(c)所示.

(a) 定义不同的采样路径
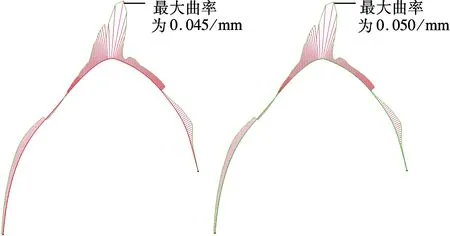
(b) 路径3曲率分析 (c) 路径4曲率分析

(4)
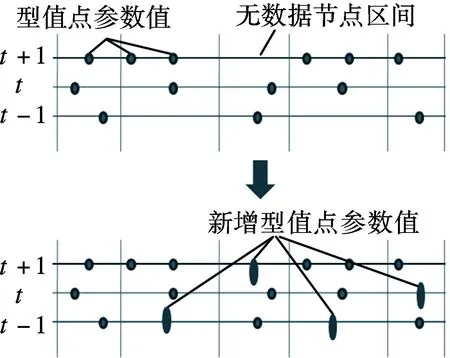
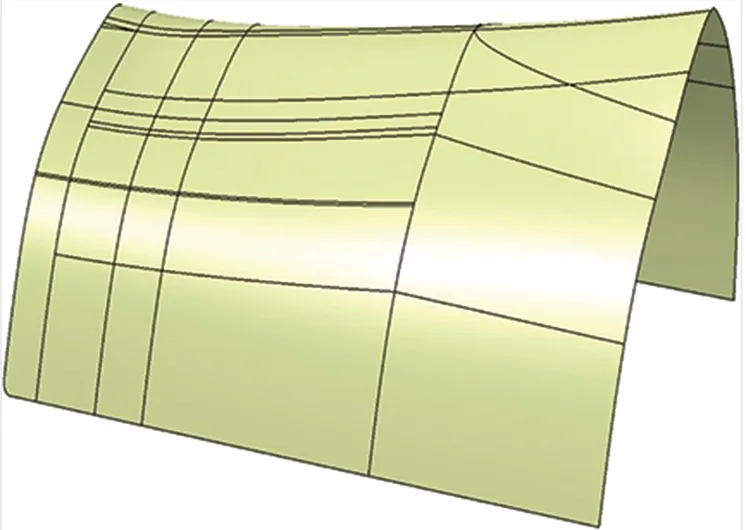
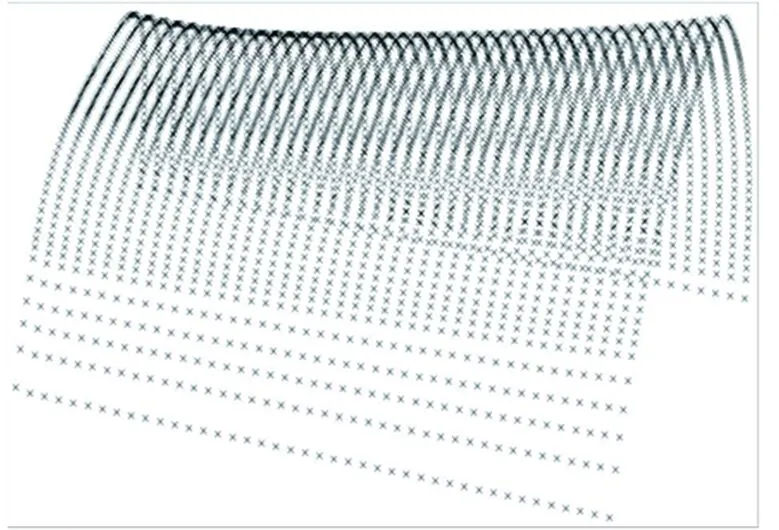
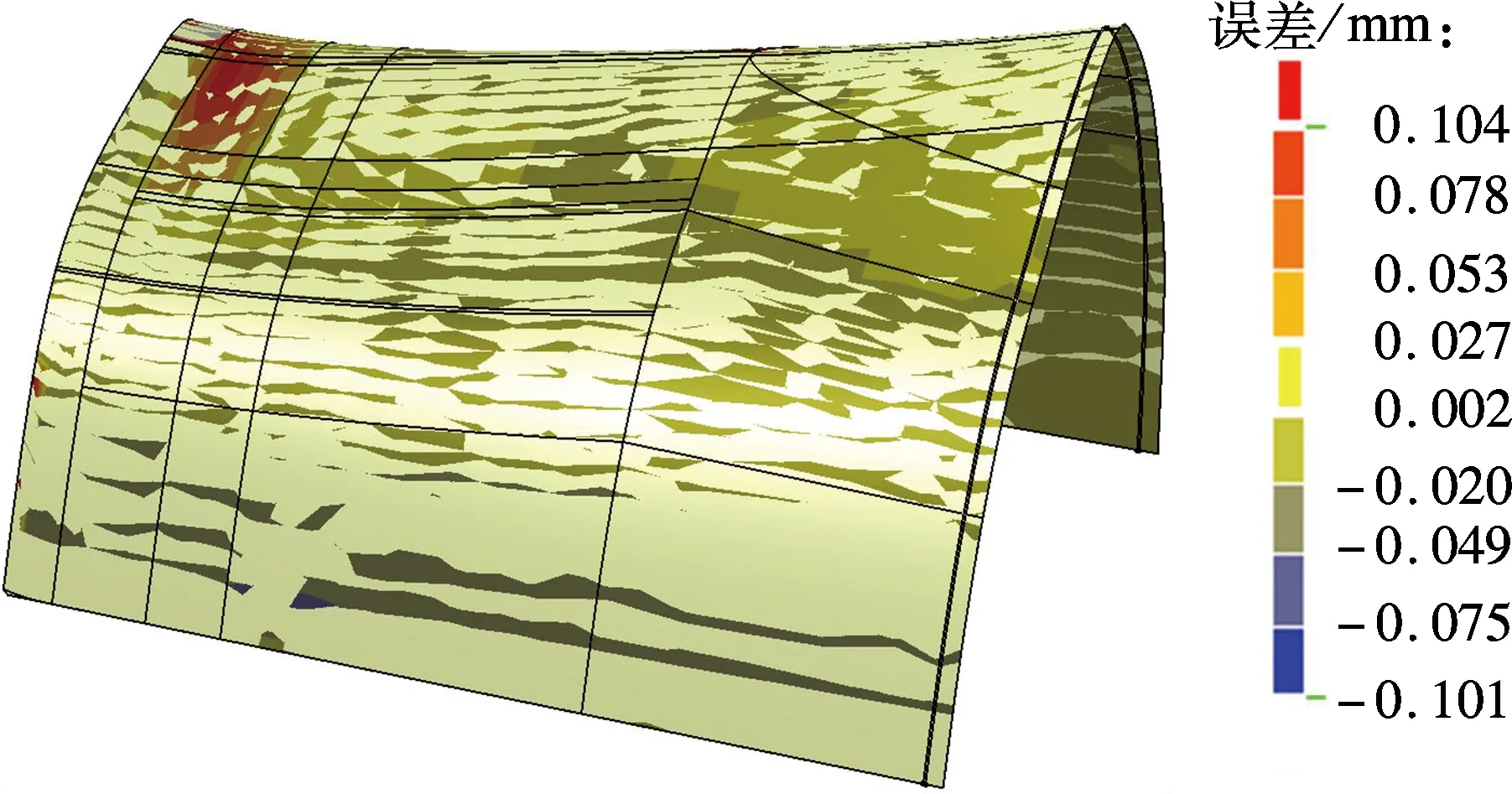
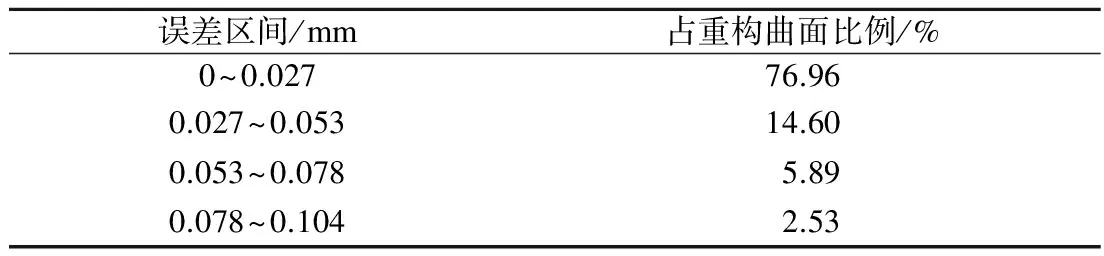
(5)式中,0≤t (6) (7) 式中,f≠p;T(ui)为端点非插值性的节点向量,应用Piegl等[1]提出的算法求解新的控制点Qi,i=0,1,…,H. (8) 式中,f+1+s=p+1,f+1+m=p+1;s为左侧节点矢量插入数量;m为右节点插入的数量.节点向量标准化为 (9) 即得到共同节点向量U(ui),实现截面线相容[10],如图3所示.根据共同节点矢量,将型值点(离散点)细化,图4中椭圆形的点即为新增的型值点. (a) 初始截面线 (b) 相容后的截面线 图4 型值点加密 在热成形模具型面的设计过程中,首先要对热成形零件曲面进行修剪、外插延伸等操作,然后再进行对应上下模体的设计.由于大多数多面片拼接的零件曲率变化较大且曲率不连续,设计人员无法直接对热成形零件曲面进行外插延伸操作,需要对零件曲面进行反复的修补达到曲面延伸的基本要求,其过程复杂,操作繁琐,且延伸后的曲面质量无法保证,影响了热成形模具的设计效率[11]. 本文将基于非端点插值NURBS曲面重构相关算法集成到热成形零件曲面延伸重构操作中,获取了连续性较好的单张曲面,减少了热成形零件表面延展过程中出现的曲面扭曲和畸形等问题,提高了设计效率.输入型值点矩阵,可通过集成后的算法计算共同节点矢量和控制点阵,实现原始拼接曲面的重构.曲面的重构过程如图5所示. (a) 原始曲面 (b) 初始型值点 (c) 型值点加密 (d) 重构曲面 对重构好的曲面进行误差分析.由图6所示的重构曲面误差分析图及表1重构曲面与原始曲面误差统计表可知, 76.96%的重构曲面与原始曲面间的误差小于0.027 mm,且曲面最大误差仅为0.104 mm,占重构后曲面比例低于2.53%,因此曲面重构精度较高. 图6 重构曲面误差分析 误差区间/mm占重构曲面比例/%0~0.02776.960.027~0.05314.600.053~0.0785.890.078~0.1042.53 本文针对拼接曲面提出了基于非端点插值理论的NUEBS曲面重构方法,详细阐述了曲面重构过程中关键参数的确定.通过易于构造的非端点插值的节点矢量,经过节点矢量的升(降)阶和节点插入(去除)算法转化为标准形式的端点插值的共同节点矢量,将确定后的共同节点矢量用于重新细化型值点,为控制点求解提供点云数据,实现了参数化NURBS曲面的重构.对重构误差进行了统计,结果表明,最大误差仅为0.104 mm,占重构后曲面的比例低于2.53%.因此基于端点非插值性的曲面重构方法具有较高的重构精度. References) [1]Piegl Les, Tiller Wayne.TheNURBSbook[M]. New York, USA:Springer,1995:60-200. [2]Boehm W. Inserting new knots into B-spline curves [J].Computer-AidedDesign, 1980, 12(4): 199-201. [3]Hu S M, Tai C L, Zhang S H. An extension algorithm for B-splines by curve unclamping [J].Computer-AidedDesign, 2002, 34(5):415-419. [4]Chen X D, Ma W Y, Paul J C. Cubic B-spline curve approximation by curve unclamping [J].Computer-AidedDesign, 2010, 42(6):523-534. [5]Zhiming X, Jincheng C, Zhengjin F. Performance evaluation of a realtime interpolation algorithm for NURBS curves [J].IntJAdvManufactTechnol, 2002, 20:270-276. [6]Cheng F B, Liu Z Y, Duan G F,et al. NURBS surface deformation design for complex products by transplanting the surface feature[J].EngineeringwithComputers, 2014, 30(4):599-608. [7]Tsai Mengshiun, Nien Haowei, Yau Hongtzong. Development of an integrated look-ahead dynamics-based NURBS interpolator for high precision machinery [J].Computer-AidedDesign, 2008, 40(5): 554-566. [8]Shi Xiquan, Wang Tianjun,Wu Peiru, et al. Reconstruction of convergent G1 smooth B-spline surfaces [J].ComputerAidedGeometricDesign, 2004, 21(9): 893-913.[9]Jiang Q Q, Wu Z K, Zhang T, et al. G(2)-continuity extension algorithm of ball B-spline curves [J].IeiceTransactionsonInformationandSystems, 2014, 97(8):2030-2037.[10]Chen H, Bishop J. Delaunay triangulation for curved surface [C]//Proceedingsofthe6thInternationalMeshingRoundtable. Park City, USA, 1997:115-127.[11]Shetty S, White P R. Curvature-continuous extensions for rational B-spline curves and surfaces [J].Computer-AidedDesign, 1991, 23(7):484-491. A reconstruction method for NURBS surface by curve unclamping Zhang Guojun Xing Yan (School of Mechanical Engineering,Southeast University, Nanjing 21189, China) To solve the poor continuity and extension of surface with multipatch splicing and dress up features, a non-uniform rational B-spline (NURBS) surface reconstruction method based on the unclamping was proposed. First, the original surface was discretized into point-cloud according to the different locations and curvatures, the knot vectors of each sampling path were calculated based on discreted points. Then, the unclamping common knot vector and the control net required for surface-reconstruction were calculated, and the unclamping common vector needed to be changed into the clamping common vector. Based on the latest clamping vector, new data points were inserted into the rectangle without data. Finally, all data points were fitted to a single surface. The reconstruction results show that the amount of calculation is reduced and the reconstructed surface has high accuracy. It can guarantee the fitting ratio and the continuity of curvature where the curvature has sharp change. During modeling, the proposed method reconstructs the original surface to a single surface, improves the precision of the surface reconstruction and solves problems, such as surface degradation and surface distortion. non-uniform rational B-spline; surface discretization; surface reconstruction; curve unclamping 10.3969/j.issn.1001-0505.2016.06.009 2016-02-16. 作者简介: 张国军(1989—),男,博士生;幸研(联系人),男,博士,教授,博士生导师,xingyan@seu.edu.cn. “十二五”某部先进制造技术预先研究资助项目(51318010102)、江苏省前瞻性联合研究资助项目(BY2015070-06). 张国军,幸研.一种基于端点非插值性的NURBS曲面重构方法[J].东南大学学报(自然科学版),2016,46(6):1161-1164. 10.3969/j.issn.1001-0505.2016.06.009. TP39 A 1001-0505(2016)06-1161-04
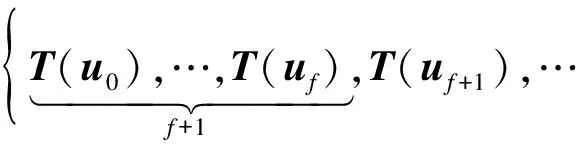

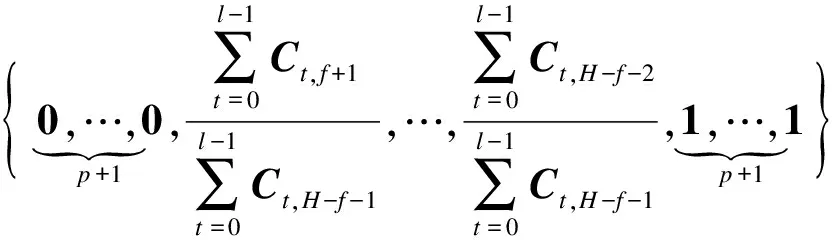

3 曲面重构方法应用


4 曲面重构误差分析
5 结语

