胶印机齿轮传动系统动力学建模及优化设计
欧阳天成 黄豪中 王 攀 陈 南
(1东南大学机械工程学院, 南京 211189)(2广西大学机械工程学院, 南宁 530004)
胶印机齿轮传动系统动力学建模及优化设计
欧阳天成1,2黄豪中2王 攀1陈 南1
(1东南大学机械工程学院, 南京 211189)(2广西大学机械工程学院, 南宁 530004)
为了提高胶印机高速印刷条件下的动态特性,针对胶印机齿轮传动系统动力学问题,建立了多级平行轴齿轮传动系统动力学模型,并对其进行动态优化设计.首先,描述了齿轮传动系统的时变啮合刚度、静态传动误差、啮合阻尼、动态啮合力和滚动轴承刚度表达式,并利用集中参数法建立了多级平行轴齿轮传动系统动力学模型;然后,运用Runge-Kutta法对齿轮传动系统动力学方程进行数值求解;最后,采用序列二次规划法对齿轮系统进行参数优化,并对其进行齿廓修形.数值计算结果表明,优化后齿轮系统的动态特性在啮合刚度、单齿载荷、动态啮合力、动态传动误差和滚筒相对滑动速度方面都有提高,为解决胶印机高速印刷条件下动态特性不良问题开拓了一条新途径.
胶印机;齿轮传动系统;动力学;参数优化;齿廓修形
多级平行轴齿轮传动装置由于其传动比准确、功率恒定和结构紧凑等特点,具有其他传动装置不可代替的优势.多色胶印机印刷装置通过多级平行轴齿轮传动系统来保持精确的运动配合与动力传递,齿轮传动系统动态特性对整机性能有重要的影响.啮合刚度激励源于齿轮啮合过程中参与啮合轮齿对数及接触参数的变化,是引起齿轮系统振动的主要原因,决定了齿轮系统动力学的基本性质以及动力学模型的研究和求解方法[1].啮合刚度激励与齿轮的几何参数紧密相关,修形是为了改善齿轮系统运行性能,良好的参数设计和适当的修形能降低齿轮系统的振动与噪声.
朱丽莎等[2]基于有限元法建立了弯-扭-轴-摆斜齿轮耦合动力学分析模型,并对系统进行了固有特性分析和不平衡响应分析,研究结果表明多齿轮系统存在强烈的耦合效应,临界转速和振动峰值需要通过固有特性以及瞬态响应分析来判断.Hua等[3]基于有限元法提出了一种改进型的集中参数螺旋锥齿轮动力学模型,建模过程中引入了等效质量和等效惯性单元概念,数值计算结果显示改进模型在求解效率和精度上都优于传统的集中参数模型.Ouyang等[4]利用集中参数法建立了包含时变啮合刚度、静态传动误差的胶印机多级平行轴齿轮传动系统动力学模型,运用Runge-Kutta法对系统进行数值求解,最后通过数值解与实验数据的对比证明了动力学模型的有效性.Rivola等[5]从实验测试和数学模型2方面对发动机气门正时系统的齿轮传动装置展开研究,实验测试检验了不同转速和设计参数对齿轮装置性能的影响,数学模型明确了系统主要部件的优化方向.Kim等[6]建立了包含齿轮驱动装置的冷辊轧机动力学模型,并通过直接积分法与准静态分析相结合求解了系统动态响应,数值分析结果显示水平方向颤振对系统动态特性有很大影响.Devendran等[7]利用遗传算法对汽车尾气后处理齿轮泵进行多目标优化设计,最大限度地提高齿轮泵的容积效率和降低噪声排放.毛万镈等[8]针对永磁接触器操动机构动态优化设计问题进行了研究,以体积、平均合闸时间和撞击能量为多目标函数,运用自适应模拟退火算法进行多目标动态优化设计.Bruyère等[9]提出一种简化分析法来评估齿廓修形对传动误差的影响,并推导了设计准则的最佳修形参数.Baglioni等[10]基于平均摩擦系数和时变摩擦系数法研究了齿顶修形对齿轮传动效率的影响,并总结出2种齿顶修形法则.
动态响应测试结果显示,高速印刷条件下胶印机的振动主要来源于齿轮传动系统[11]. 因此,本文在建立胶印机齿轮传动系统动力学模型的基础上,利用数值法求取了系统动态响应,并分析了动力学特性,对其进行优化设计,得到了动态性能更好的多级平行轴齿轮传动系统.
1 动力学模型
胶印机多级平行轴齿轮传动系统如图1所示,齿轮1,2,3,4分别为传纸滚筒斜齿轮、压印滚筒斜齿轮、橡皮滚筒斜齿轮和印版滚筒斜齿轮,斜齿轮通过螺栓与滚筒连接轴进行固接.印刷过程中纸张沿X方向传递,Y方向为竖直方向,齿轮轴向方向与Z方向平行.
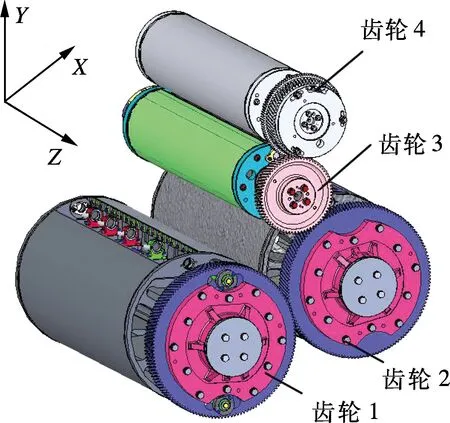
图1 多级平行轴齿轮传动系统三维图
在结构简化基础上,把啮合齿轮视为时变刚度弹簧,支承轴承处理为等效刚度弹簧,将滚筒的平动质量向齿轮中心简化,利用集中参数法建立胶印机多级平行轴斜齿轮动力学模型.
如图2所示,平行轴斜齿轮为4级传动系统.斜齿轮1~4存在沿Y方向的弯曲位移、Z方向的轴向位移和绕Z方向的扭转位移;每个滚筒都存在绕Z方向的扭转位移,斜齿轮通过具有扭转刚度的弹性轴与滚筒连接.在每一级传动中,斜齿轮有2个平动和1个转动自由度,滚筒只有1个转动自由度.具有16个自由度的胶印机多级平行轴斜齿轮动力学模型节点位移向量为

图2 多级平行轴斜齿轮动力学模型
q={θ1,y1,z1,θg1,θ2,y2,z2,θg2,θ3,
y3,z3,θg3,θ4,y4,z4,θg4}T
(1)
式中,θi为斜齿轮绕Z方向转角;yi为斜齿轮沿Y方向位移;zi为斜齿轮沿Z方向位移;θgi为滚筒绕Z方向转角;i=1,2,3,4.
1.1 啮合刚度、静态传动误差和啮合阻尼
啮合刚度激励是引起齿轮系统振动的主要原因,本文采用Cai[12]的拟合公式来计算胶印机多级平行轴斜齿轮的啮合刚度.斜齿轮单对轮齿啮合刚度计算公式为
(2)
式中,bw为有效齿宽;β为分度圆螺旋角;ε为总重合度;εa为端面重合度;H为全齿高;t为齿轮啮合时间;tz为齿轮啮合周期(转过一个端面基圆节距的时间);mn为法向模数;xn1,xn2分别为主动轮和从动轮的法向变位系数;zv1,zv2分别为主动轮和从动轮的当量齿数;c0为偏移系数;c0,c1,…,c5为拟合系数.
多级平行轴斜齿轮时变啮合刚度为
(3)
式中,n为同时参与啮合的轮齿对数;ij为下标组合(ij=12, 23, 34).
静态工况条件下由齿轮变形和齿轮误差所引起的啮合误差称为静态传动误差[13],静态传动误差属于周期函数,其谐波函数表达式为
(4)
式中,e0为静态传动误差平均值;en为静态传动误差谐波项幅值;νn为静态传动误差谐波项啮合相位;ωm为齿轮啮合频率(ωm=ωizi,ωi为主动轮转速,zi为主动轮齿数).
多级平行轴斜齿轮啮合阻尼计算公式为
(5)
式中,kave为齿轮平均啮合刚度;ri,rj分别为主动轮和从动轮基圆半径;Ji,Jj分别为主动轮和从动轮的转动惯量;ξg为齿轮啮合阻尼比(取ξg=0.05).
1.2 动态啮合力
齿轮系统在内部与外部激励的共同作用下形成波动啮合力,斜齿轮啮合副动力学模型如图3所示.斜齿轮啮合副的切向与轴向动态啮合力分别为
(6)

图3 斜齿轮啮合副动力学模型
(7)
如图3所示,斜齿轮啮合过程中的径向与轴向相对位移分别为
(8)
斜齿轮通过弹性轴与滚筒相连接,由于滚筒的转动惯量较大,运行过程中二者不完全同步,因而存在相互力矩作用.斜齿轮对滚筒的扭转力矩为
Tθi=(θi-θgi)kθi
(9)
式中,kθi为滚筒连接轴的扭转刚度,i=1,2,3,4.
1.3 滚动轴承刚度
在外载荷作用下,滚动轴承内、外滚道与钢球发生接触,根据Hertz弹性接触理论得到钢球接触变形与外载荷的关系式为
(10)
式中,Q为外载荷;Kn为Hertz刚度系数;δn为内外滚道之间总的法向接触变形;b为计算系数(对于球轴承b=1.5,对于圆柱滚子轴承b=1.11).
基于轴承接触角不随载荷改变的假设条件,忽略了间隙的滚动轴承径向与轴向刚度分别为[14]
(11)式中,ky,kz分别为轴承径向刚度和轴向刚度;Z为滚子个数;Jr为余弦计算系数;δr为内外圈的径向相对位移;δa为内外圈的轴向相对位移;αc为接触角.
1.4 动力学方程
根据达朗贝尔原理得到具有16个自由度的多级平行轴斜齿轮动力学方程,其表达式为
(12)

2 优化设计
胶印机多级平行轴齿轮传动系统优化设计包括几何参数优化与齿廓修形2部分.几何参数优化的首要任务是建立一个切合实际的数学模型,然后确定目标函数、设计变量以及约束条件,并选择有效的优化算法进行优化迭代.齿廓修形主要包括修缘与修根,修缘是对齿顶部分的齿廓进行修形.修缘是降低齿轮振动、减小动载荷和改善齿面润滑的有效手段,尤其是在消除啮合冲击方面效果十分明显.
2.1 几何参数优化
啮合刚度波动是导致齿轮传动系统振动的主要原因,本文选取单个啮合周期的啮合刚度波动标准差作为齿轮传动系统参数优化的目标函数,其表达式为
(13)
式中,f为啮合刚度波动标准差的等效值;kave, ij为第ij级的齿轮平均啮合刚度;N为单个啮合周期的啮合刚度离散点数.
中心距与传动比在齿轮参数优化中保持不变;依据无齿侧间隙准则,各级传动齿轮之间的变位系数成一定关系.基于以上两点,只需要确定其中一个齿轮的齿数和变位系数,就可以得到其他齿轮的齿数和变位系数.多级平行轴齿轮参数优化的设计变量为:模数mn、齿数z1、压力角α、螺旋角β、齿顶高系数fa和法向变位系数x1.z1和x1分别是斜齿轮1的几何参数.设计变量向量表达式为
X=[mn,z1,α,β,fa,x1]
(14)
采纳文献[15]给出的多级平行轴斜齿轮参数优化的约束条件,包括模数、齿数、压力角、螺旋角、齿顶高系数和法向变位系数的上、下限,以及齿轮啮合不干涉、齿面接触疲劳强度和齿根弯曲疲劳强度.
2.2 齿廓修形
修缘是人为地在齿轮的齿顶处修去由变形误差、齿形误差等引起的啮合干涉量,从而降低啮合过程中的动载荷.如图4所示,修缘的三大要素分别为最大修形量、修形长度和修形曲线.

图4 齿轮修缘示意图
齿廓修形的理论最大修形量为
δmax=δ+δθ+δm
(15)
式中,δ为受载弹性变形;δθ为齿轮热变形;δm为制造误差.
根据ISO 6336齿轮强度标准[16],齿轮受载弹性变形计算式为
(16)
式中,KA为工况系数;Ft为啮合切向力;Ck为综合啮合刚度.
齿轮啮合热变形计算式为
δθ=πmncosαΔθγ
(17)
式中,Δθ为啮合轮齿的温度差;γ为材料线膨胀系数.高速胶印机齿轮传动系统采用长修形,修形长度L(从双齿啮合起点B1到啮合终点D)如图4所示.
Walker[17]推荐的修形曲线为
(18)
式中,x为啮合位置的相对坐标,原点是双齿啮合起点B1(见图4);δx为距离x处的修形量.
3 优化结果分析
本文在最高转速下(15 000 r/h),利用序列二次规划法对多级平行轴齿轮系统进行优化设计,优化结果将圆整到标准值或保留有限位小数.表1给出了多级平行轴斜齿轮优化前后的部分几何参数,参数优化后斜齿轮的模数减小而齿数增多,压力角减小,而螺旋角和齿顶高系数增大.表2给出了多级平行轴斜齿轮齿廓修缘的最大修形量和修形长度.
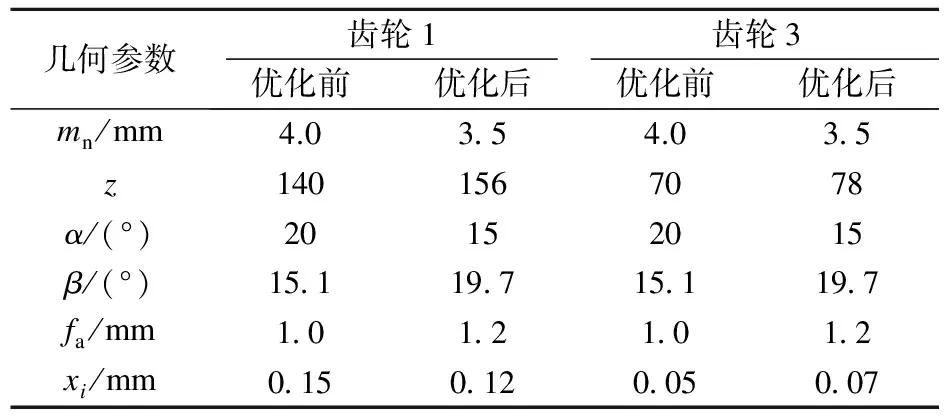
表1 优化前后斜齿轮几何参数

表2 斜齿轮修形参数
3.1 啮合刚度
啮合刚度波动的大小对齿轮系统动态特性有很大影响,参数优化的目标是减小啮合刚度波动,优化前后的啮合刚度如图5所示.从图5(a)可以看出,优化前啮合刚度在单齿啮合转变为双齿啮合区存在突变,优化后啮合刚度突变减小,且波动值小于优化前.图5(b)显示,啮合刚度优化前的波动幅值约为93 MN/m,优化后为61 MN/m,下降了34%.
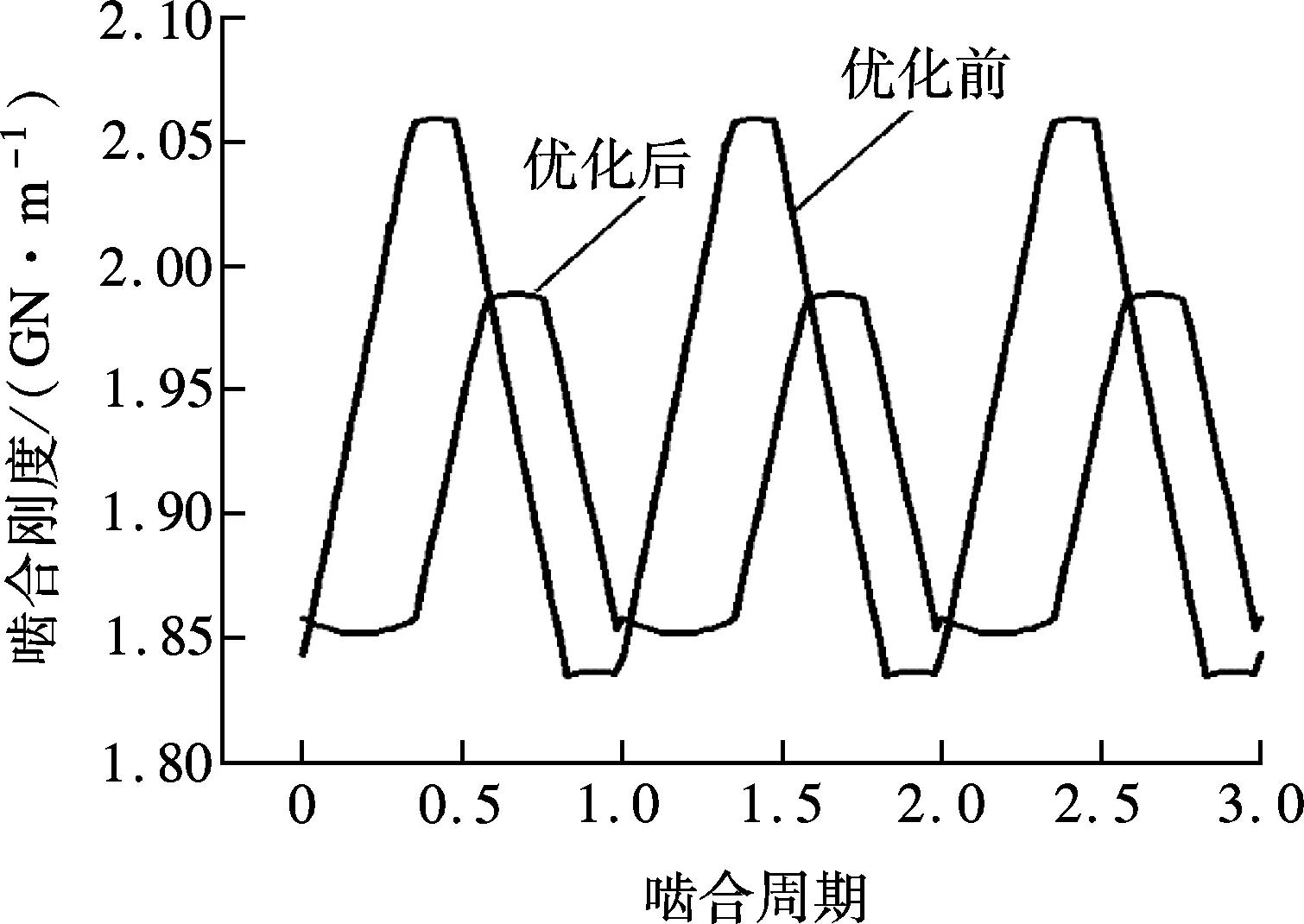
(a) 齿对12

(b) 齿对23
3.2 单齿载荷
转速为15 000 r/h时,优化设计前、后单个轮齿的载荷加载过程如图6所示.图6(a)显示,参数优化前斜齿轮在啮入点的载荷从60 N/mm开始加载,初始啮入过程的载荷变动剧烈,有明显的“高瘦型”峰值;载荷在啮合区中部分有波动;在啮出时载荷先是增大并达到峰值,然后出现大幅度下降直至退出啮合.优化后斜齿轮在啮入点的载荷从10 N/mm开始加载,然后缓慢增加载荷直到峰值;载荷在啮合区中部分相对比较平缓;在啮出段载荷缓慢减小直至退出啮合.单齿加载显示,优化后斜齿轮在啮合线长度、初始载荷量、载荷变动幅度和变动速率方面都得到了改善.
通过图6(a)和(b)的比对发现,齿对23的单齿加载过程与齿对12的加载过程有类似趋势,但齿对23的载荷在啮合区中部存在明显的波动.
3.3 动态啮合力
转速为15 000 r/h时,优化前、后斜齿轮对12的动态啮合力如图7所示.通过图7(a)与(b)的对比发现,优化前、后的平均啮合力几乎不变(约8.7 kN),优化前啮合力的波动幅值约为4.4 kN,优化后啮合力的波动幅值接近3.55 kN,波动幅值下降了19.3%左右.
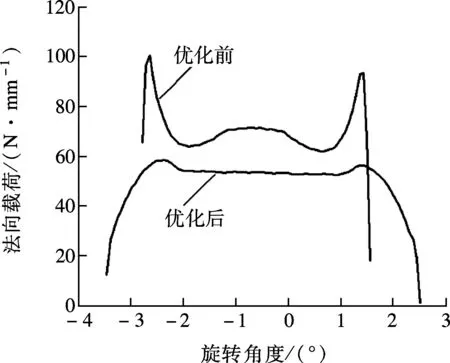
(a) 齿对12

(b) 齿对23
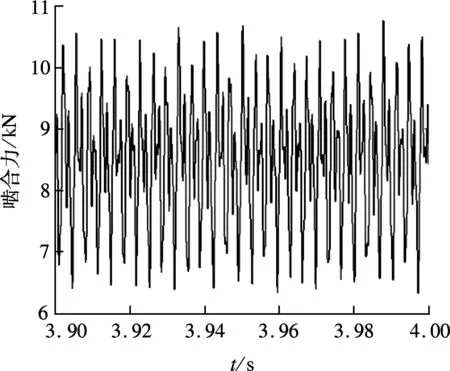
(a) 优化前

(b) 优化后
3.4 动态传动误差
动态传动误差是轮齿实际啮合位置与理想啮合位置的偏差,动态传动误差的大小是衡量齿轮系统动态特性的一个重要指标[18].转速为15 000 r/h时,优化前、后斜齿对12的动态传动误差如图8所示.图8显示,优化前动态传动误差的最大值接近6.3 μm,平均值约为5.2 μm;优化后动态传动误差的最大值下降到5.1 μm,平均值约为4.3 μm.数值计算结果证明了齿轮优化设计取得了良好的效果.

(a) 优化前

(b) 优化后
3.5 滚筒相对滑动速度
纸张印刷过程中,接触滚筒表面线速度的同步性是套印精度的保证.滚筒表面的相对滑动速度要控制在一定范围内,否则将会在印刷品上留下墨杠或重影.在转速范围为4 000~15 000 r/h时,优化设计前、后橡皮-压印滚筒相对滑动速度如图9所示.图9显示,滚筒的相对滑动速度随转速的提高而增大,优化设计后滚筒的相对滑动速度有所下降.最高印刷速度下(15 000 r/h),优化前滚筒的相对滑动速度波动幅值接近于1.7 mm/s;优化后滚筒的相对滑动速度波动幅值下降到1.46 mm/s,优化后齿轮传动系统动态特性有所提高.

图9 橡皮-压印滚筒相对滑动速度
4 结语
为了提高胶印机高速印刷条件下的动态特性,本文在建立多级平行轴齿轮传动系统动力学模型基础上,利用数值法求取了系统动态响应,并对齿轮传动系统进行了动态优化设计.优化设计结果表明,减小啮合刚度的波动能有效提高齿轮传动系统动态特性.齿轮优化后,单齿加载过程得到了改善,动态啮合力波动幅值有所下降,动态传动误差和滚筒相对滑动速度都相应减小.
References)
[1]Chen Y C, Kang C H, Choi S T. Vibration analysis of geared rotor system under time varying mesh stiffness effects [J].JournalofVibroengineering, 2012, 14(3): 1141-1150.
[2]朱丽莎, 张义民, 马辉, 等. 多齿轮耦合复杂转子系统的振动特性分析 [J]. 振动与冲击, 2013, 32(14): 34-39. DOI:10.3969/j.issn.1000-3835.2013.14.006. Zhu Lisha, Zhang Yimin, Ma Hui, et al. Vibration behavior analysis of a complex rotor system with coupled multi-gear system [J].JournalofVibrationandShock, 2013, 32(14): 34-39. DOI:10.3969/j.issn.1000-3835.2013.14.006. (in Chinese)
[3]Hua X, Lim T C, Peng T, et al. Dynamic analysis of spiral bevel geared rotor systems applying finite elements and enhanced lumped parameters [J].InternationalJournalofAutomotiveTechnology, 2012, 13(1): 97-107. DOI:10.1007/s12239-012-0009-4.
[4]Ouyang T C, Chen N, Yin G D. On modeling of offset press gear transmission system and parameter optimization [J].JournalofVibrationEngineeringandTechnologies, 2015, 3(3): 355-367.
[5]Rivola A, Troncossi M. Dynamic analysis of a motorbike engine timing system: Experimental and numerical investigation of the geartrain [J].MechanicalSystemsandSignalProcessing, 2014, 48(1): 325-338. DOI:10.1016/j.ymssp.2014.03.008.
[6]Kim Y, Park H, Lee S S, et al. Development of a mathematical model for the prediction of vibration in a cold rolling mill including the driving system [J].ISIJInternational, 2012, 52(6): 1135-1144. DOI:10.2355/isijinternational.52.1135.
[7]Devendran R S, Vacca A. Optimal design of gear pumps for exhaust gas aftertreatment applications [J].SimulationModellingPracticeandTheory, 2013, 38: 1-19. DOI:10.1016/j.simpat.2013.06.006.
[8]毛万镈, 林鹤云, 汪先兵, 等. 永磁接触器操动机构多目标动态优化设计 [J]. 东南大学学报(自然科学版), 2009, 39(2): 287-292. Mao Wanbo, Lin Heyun, Wang Xianbing, et al. Multi-objective dynamic optimization design of permanent magnet actuator for contactor [J].JournalofSoutheastUniversity(NaturalScienceEdition), 2009, 39(2): 287-292. (in Chinese)
[9]Bruyère J, Velex P. A simplified multi-objective analysis of optimum profile modifications in spur and helical gears [J].MechanismandMachineTheory, 2014, 80: 70-83. DOI:10.1016/j.mechmachtheory.2014.04.015.
[10]Baglioni S, Cianetti F, Landi L. Influence of the addendum modification on spur gear efficiency [J].MechanismandMachineTheory, 2012, 49: 216-233. DOI:10.1016/j.mechmachtheory.2011.10.007.
[11]李文威. 高速多色胶印机多学科综合优化设计 [D]. 南京: 东南大学机械工程学院, 2012.
[12]Cai Y. Simulation on the rotational vibration of helical gears in consideration of the tooth separation phenomenon (a new stiffness function of helical involute tooth pair) [J].JournalofMechanicalDesign,TransactionsoftheASME, 1995, 117(3): 460-469. DOI:10.1115/1.2826701.
[13]李润方, 王建军. 齿轮系统动力学——振动、冲击与噪声 [M]. 北京: 科学出版社, 1997: 13-14.
[14]罗继伟, 罗天宇. 滚动轴承分析计算与应用 [M]. 北京: 机械工业出版社, 2009: 90-91.
[15]欧阳天成. 高速胶印机齿轮传动系统非线性动力学及弹流润滑研究 [D]. 南京: 东南大学机械工程学院, 2016.
[16]朱孝录. 齿轮传动设计手册 [M]. 2版. 北京: 化学工业出版社, 2009: 143-144.
[17]Walker H. Gear tooth deflection and profile modification [J].Engineer, 1940, 170(4414): 102-104.
[18]Tamminana V K, Kahraman A, Vijayakar S. A study of the relationship between the dynamic factors and the dynamic transmission error of spur gear pairs [J].JournalofMechanicalDesign,TransactionsoftheASME, 2007, 129(1): 75-84. DOI:10.1115/1.2359470.
Dynamics modeling and dynamic optimization design for offset press gear transmission system
Ouyang Tiancheng1,2Huang Haozhong2Wang Pan1Chen Nan1
(1School of Mechanical Engineering, Southeast University, Nanjing 211189, China)(2College of Mechanical Engineering, Guangxi University, Nanning 530004, China)
To improve the dynamic characteristics of offset press under high-speed printing, a dynamics model for the multistage parallel-axes gear transmission system, dealing with the dynamics of the offset press gear transmission system, was proposed and dynamic optimization design was carried out. First, the formulas of time-varying meshing stiffness, static transmission error, meshing damping, dynamic meshing force, and rolling bearing stiffness of the gear transmission system were described, and then the dynamics model for the multistage parallel-axes gear transmission system was established by using the lumped parameter method. Secondly, the Runge-Kutta method was used to solve the motion equations of the gear transmission system. Finally, the parameters of the gear system were optimized by using the sequential quadratic programming method, and then the profile modification was performed. The numerical results show that the dynamic characteristics of the gear system are improved in terms of the meshing stiffness, the individual tooth force, the dynamic meshing force, the dynamic transmission error and the sliding velocity between rollers. Thus, it can solve problems of the poor dynamic characteristics of offset press under high-speed printing.
offset press; gear transmission system; dynamics; parameter optimization; profile modification
10.3969/j.issn.1001-0505.2016.06.011
2016-02-03. 作者简介: 欧阳天成(1986—), 男, 博士生; 陈南 (联系人),男, 博士, 教授, 博士生导师, nchen@seu.edu.cn.
国家重大科技专项基金资助项目 (2013ZX04012032)、江苏省科技成果转化专项基金资助项目 (BA2014110)、广西省自然科学基金杰出青年基金资助项目 (2014GXNSFGA118005).
欧阳天成,黄豪中,王攀,等.胶印机齿轮传动系统动力学建模及优化设计[J].东南大学学报(自然科学版),2016,46(6):1172-1178.
10.3969/j.issn.1001-0505.2016.06.011.
TH132.41
A
1001-0505(2016)06-1172-07

